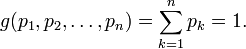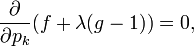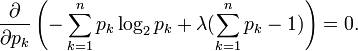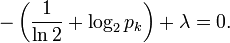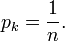拉格朗日乘子法

拉格朗日乘数

 

详细的解释见wiki，

http://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%95%B0

 

例子

[编辑]很简单的例子

求此方程的最大值：

f(x,y) = x²y

同时未知数满足

x² + y² = 1

因为只有一个未知数的限制条件，我们只需要用一个乘数λ.

g(x,y) = x² + y² − 1

Φ(x,y,λ) = f(x,y) + λg(x,y) = x²y + λ(x² + y² − 1)

将所有Φ方程的偏微分设为零，得到一个方程组，最大值是以下方程组的解中的一个：

2xy + 2λx = 0

x² + 2λy = 0

x² + y² − 1 = 0

[编辑]另一个例子

求此离散分布的最大熵：

所有概率的总和是1，因此我们得到的约束是g（p）= 1即

可以使用拉格朗日乘数找到最高熵（概率的函数）。对于所有的k 从1到n，要求

由此得到

计算出这n个等式的微分，我们得到：

这说明p_i都相等 (因为它们都只是λ的函数). 解出约束∑_k p_k = 1，得到

因此，使用均匀分布可得到最大熵的值。

通过 Wiz 发布