

1 引 言
1.1 研究背景:
至今,我们讨论的数字系统中只有一个抽样率。但是,在实际应用中,各系统之间的采样率往往是不同的。 使用多相表示可在抽样率转换的过程中去掉许多不必要的计算,因而大大提高运算速度。
1.2 研究目的:
要求一个数字系统能工作在“多抽样率(multirate)”状态,以适应不同抽样信号的需要。对一个数字信号,能在一个系统中以不同的抽样频率出现。
1.3 研究内容:
核心内容:信号抽样率的转换及滤波器组。
信号的“抽取(decimatiom) ” :减少抽样率以去掉过多数据
信号的“插值(interpolation) ” :增加抽样率以增加数据
滤波器组:分析滤波器组和综合滤波器组
%=============================================================================================================================
2 信号的抽取
2.1 抽取对信号频谱的影响 :
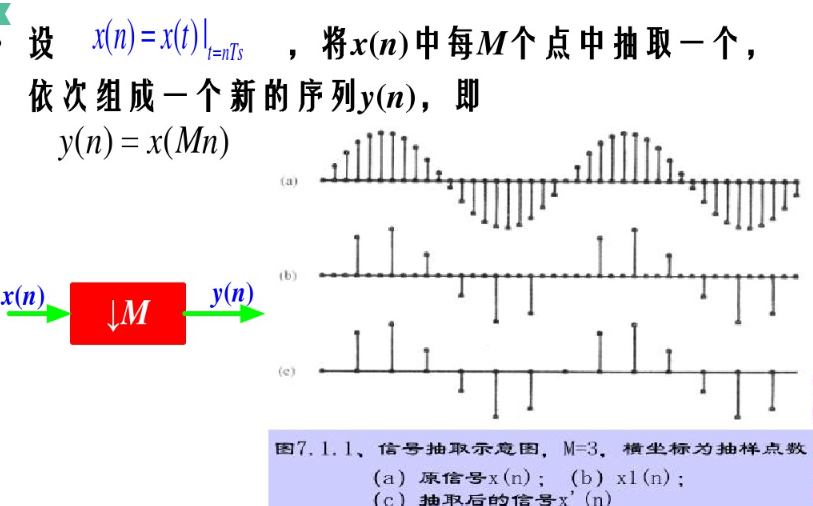

2.2 先滤波再抽取:

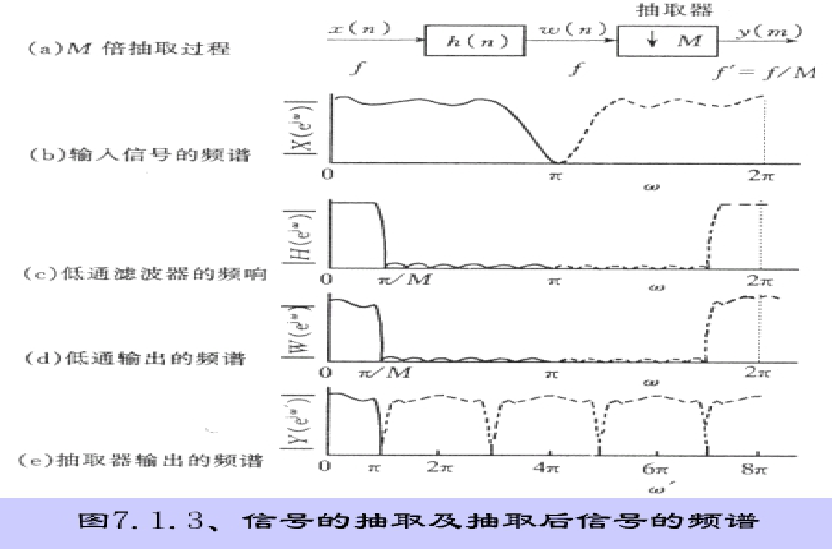

%=====================================================================================================================
3 信号的插值
3.1 插值的概念:
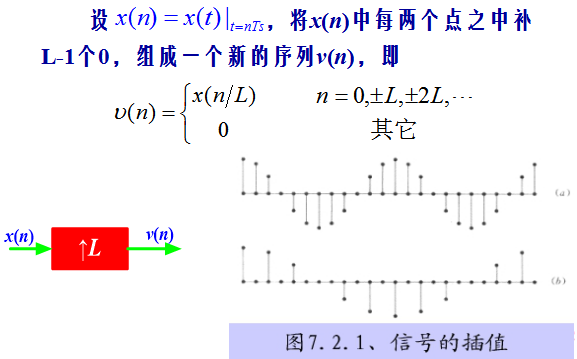
3.2 插零后的信号及其频谱
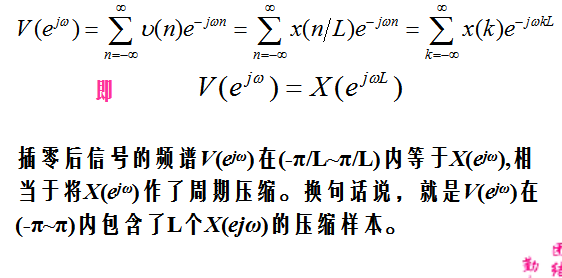
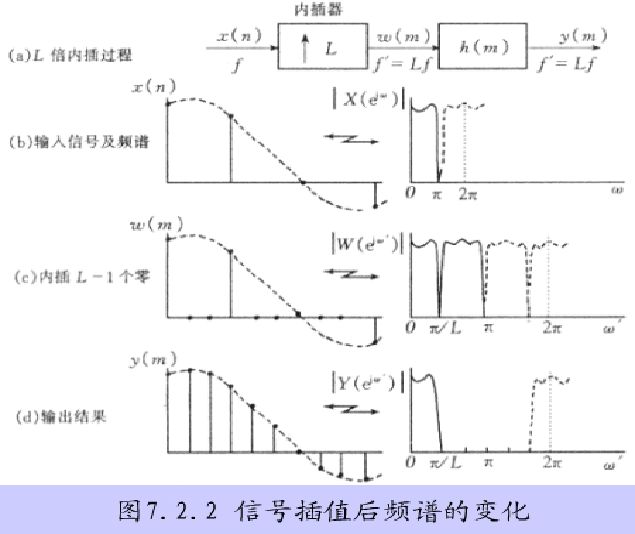
3.3 先插值再滤波


%===========================================================================================================================
4 抽取与插值相结合的抽样率转换

4.1 时域上x(n)和y(n)的关系:


4.2 频域上x(n)和y(n)的关系
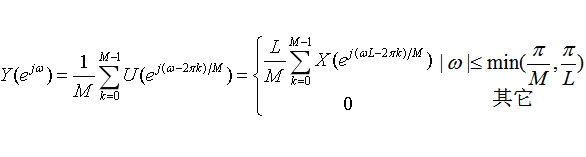
%==========================================================================================================================
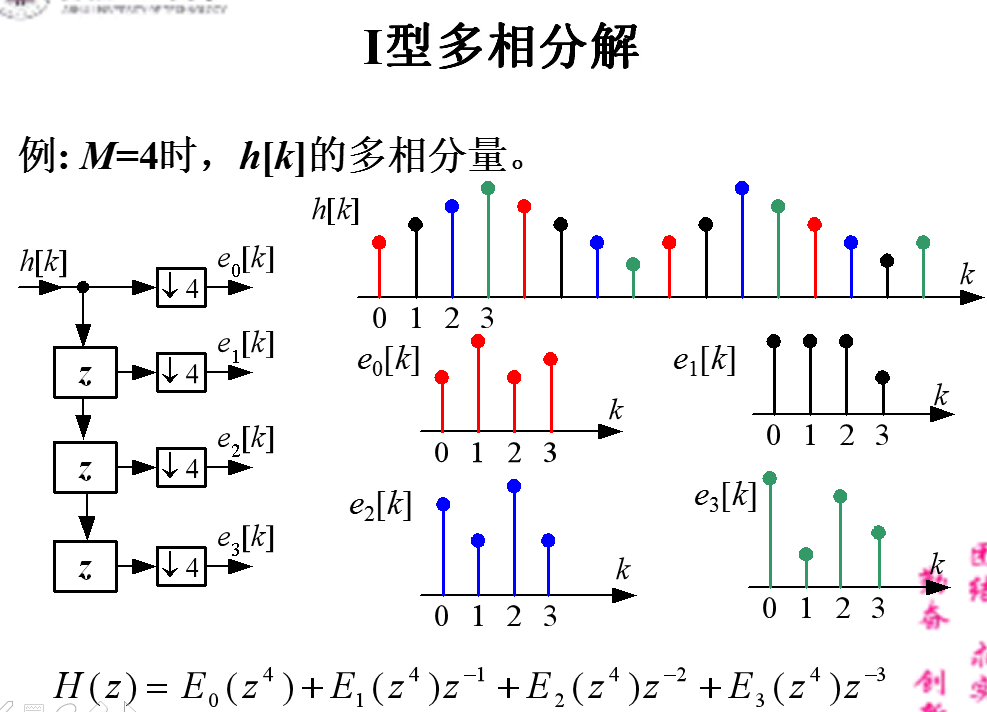
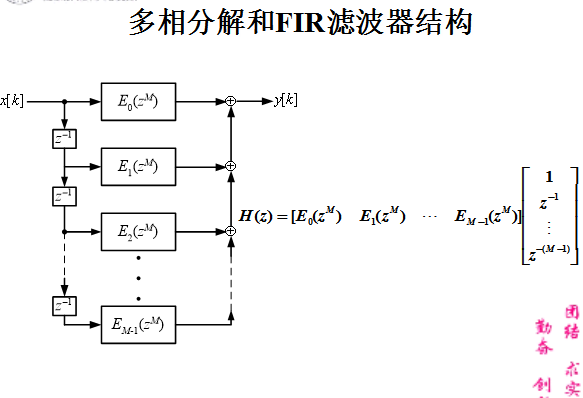
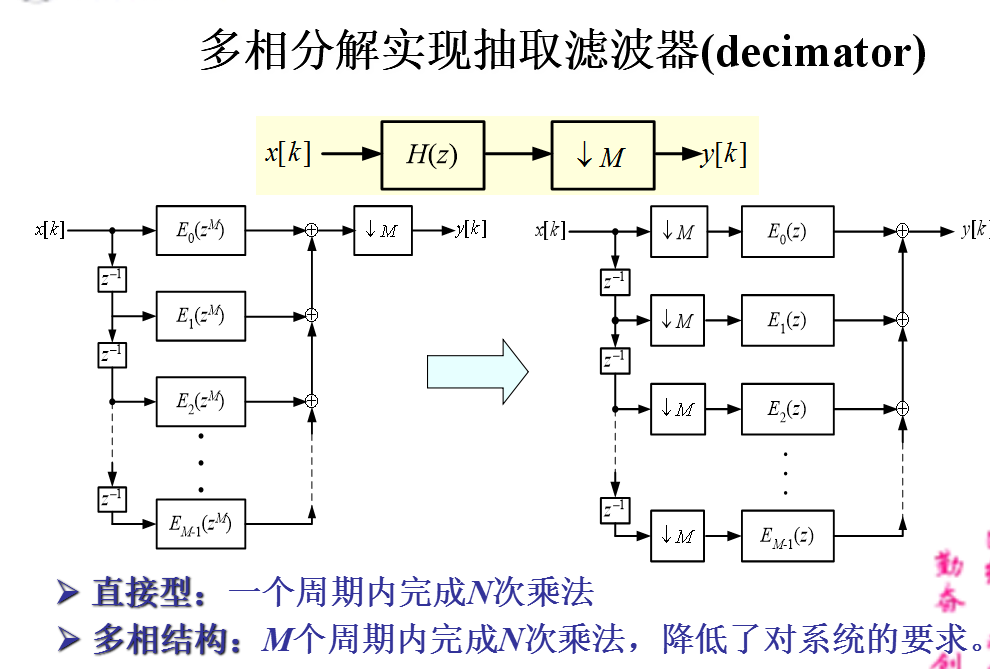
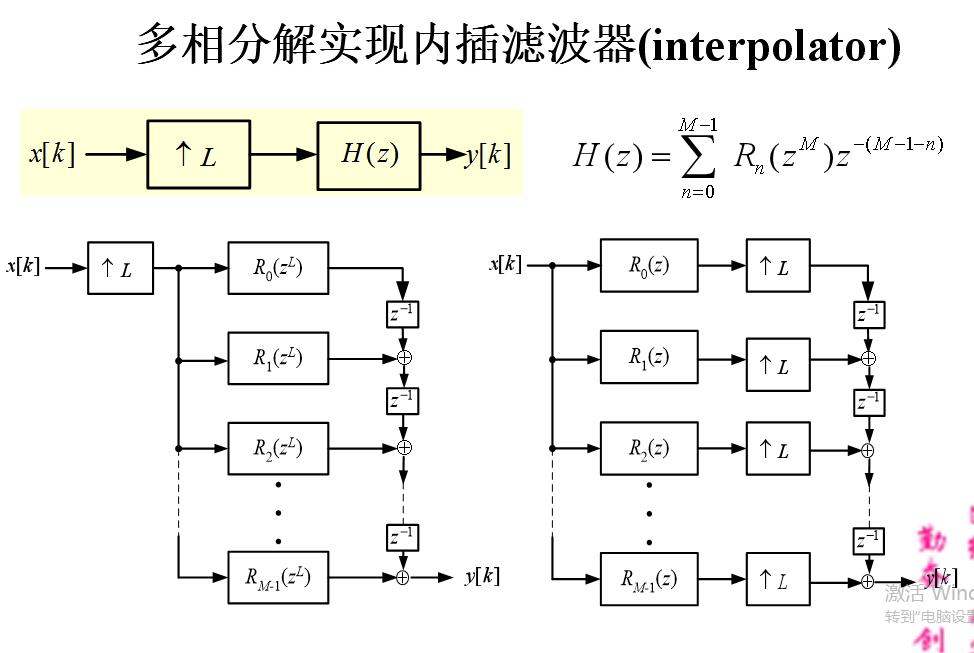
5 信号的多相表示
意义:使用多相表示可在抽样率转换的过程中去掉许多不必要的计算,因而大大提高运算速度。




-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

%==================================================================================================================================
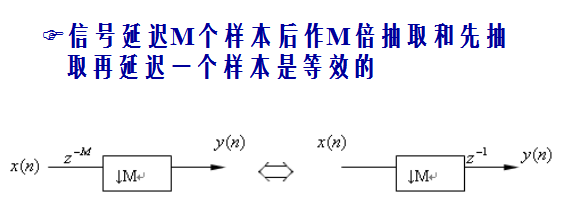
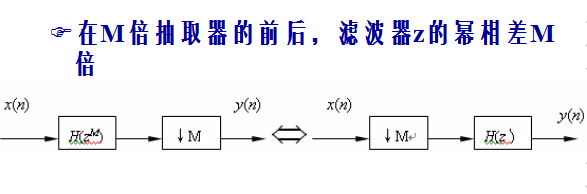
6 几个重要的恒等关系

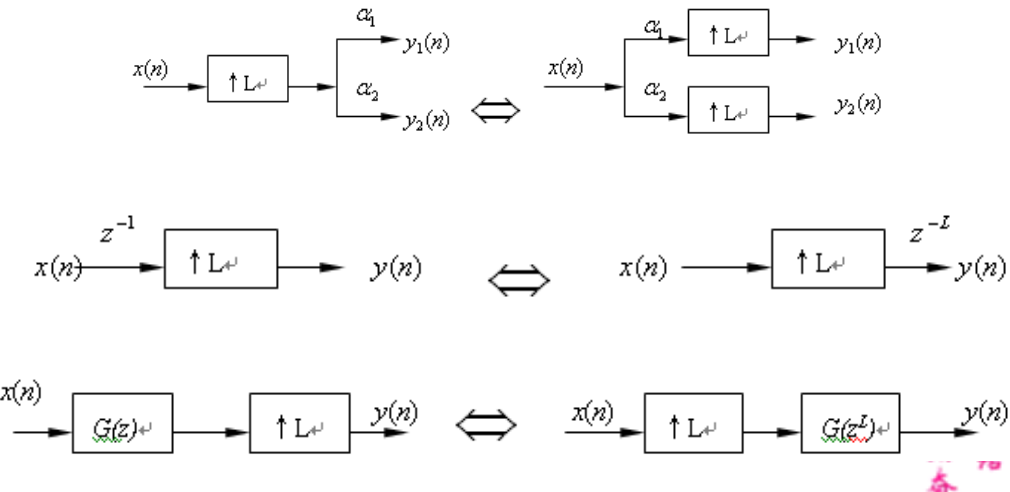
%===========================================================================================================================
7 抽取和插值的滤波器实现
7.1 抽取的滤波器实现

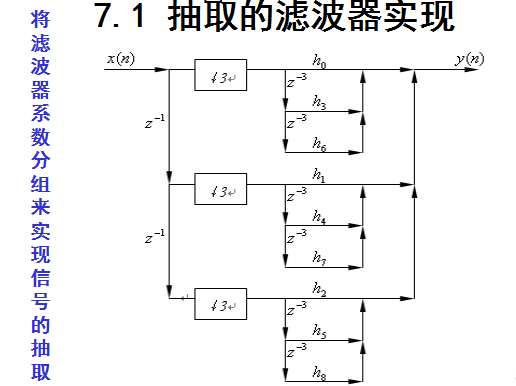

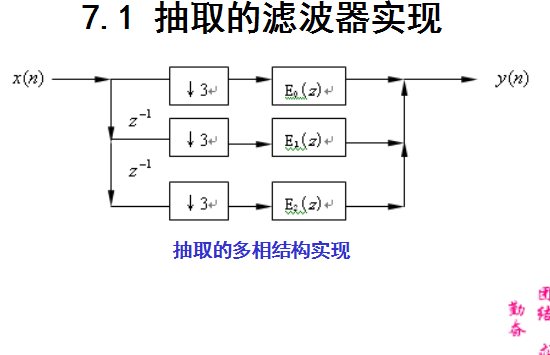
7.2 插值的滤波器实现


7.3 抽取和插值相结合的滤波器实现
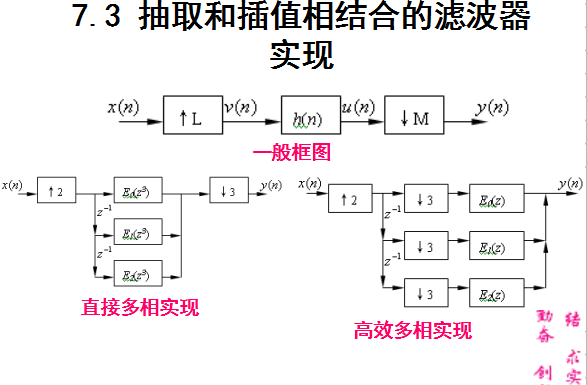
%======================================================================================================================
8 抽取与插值的编程实现



%============================================================================================================================
%先定义一个函数
function s=dchirp(TW,p)
%% generate a sampled chirp signal
N=p*TW; alpha=1/(2*p*p*TW);
n=1:N;
s=exp(j*2*pi*alpha*(n-N/2).^2); % s=exp(j*2*pi*alpha*(n-N/2).^2);
%=============================================================================================================================
%% 抽取比等于滤波器的组数
%%%研究不同抽取比下的性能
clear;clc;close all;
%% 产生线性调频信号
p=200/10;
TW=51.2;
s=dchirp(TW,p); %chirp,用法为:Y = CHIRP(T,F0,T1,F1) ,dchrip是自定义函数,
s=s.*exp(j*(pi/4)*(1:1024)); %采了1024个点
figure(1)
T=5.12e-6; %5.12*10^-6,采样总时间
N=p*TW; %N=20*51.2=1024,总采样点。但是p*TW的意义是什么
t=[-T/2:T/N:T/2];t(end)=[]; %N/T是采样率,采样间隔:T/N
plot(t*1e6,real(s));
xlabel('时间/mus'),ylabel('幅度');title('线性调频信号');grid on;

%======================================================================================================================
figure(2)
fs=p*TW/T;
y=fft(s);
y=fftshift(y);
N1=length(y);
f=[-N1/2:N1/2]/N1*fs;f(end)=[];
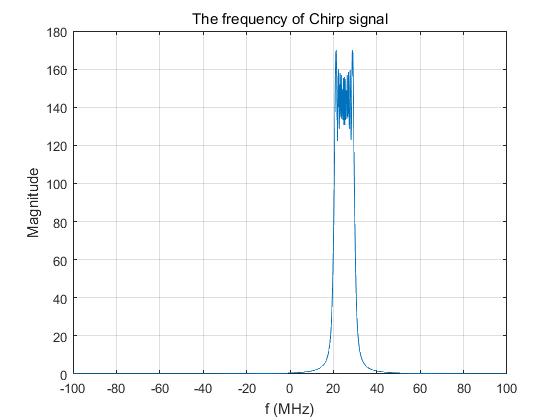
plot(f/1e6,abs(y)),grid on
title('The frequency of Chirp signal');xlabel('f (MHz)'),ylabel('Magnitude');
%=========================================================================================================================
%% 得到低通滤波器
[no,fo,mo,w]=firpmord([12.5e6,25e6],[1,0],[0.01,0.1],fs); %最佳FIR滤波器阶数估计
%最低阶低通滤波器通带截止频率是12.5e6 Hz,阻带截止频率25e6 Hz,f1=[a,b])
%a是设计滤波器时的通带,阻带的幅度,一般都是向量。我看的例子都是设为[1,0]
%通带波纹小于(rp)dB,阻带衰减大于(rs)dB,dev = [(10^(rp/20)-1)/(10^(rp/20)+1) 10^(-rs/20)];)
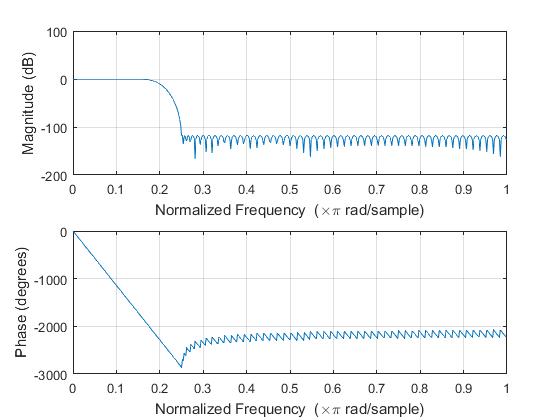
b=firpm(127,fo,mo,w);
figure(3)
freqz(b);
%=======================================================================================================================
%% 得到本振
f0=25e6;
l=exp(-j*(2*pi*f0*([-N/2:N/2-1]/fs)));
%本征频率有时也称为特征频率,固有频率,本振频率等,是一个或一组能够以纯正弦或余弦三角函数的角度参数表示的频率参数,
%是表表示所研究对象内在属性的一种参数。
%=====================================================================================================================
%% 直接下变频,用于与多相滤波比较
Y0=s.*l;
Y1=conv(Y0,b);
Y2=decimate(Y1,4); %抽样,功能:对时间序列进行整数倍采样处理,使得时间序列的长度降低。 格式:
%y = decimate(x, r),将时间序列x的采样频率降低为原来的1/r,即length(y)=length(x)/r。
%在抽取之前,默认地采用了8阶chebyshevI型低通滤波器压缩频带。
Yjw=fft(Y2);
Yjw=fftshift(Yjw);
figure(5)
N2=length(Yjw);
f=[-N2/2:N2/2]/N2*fs/4;f(end)=[];
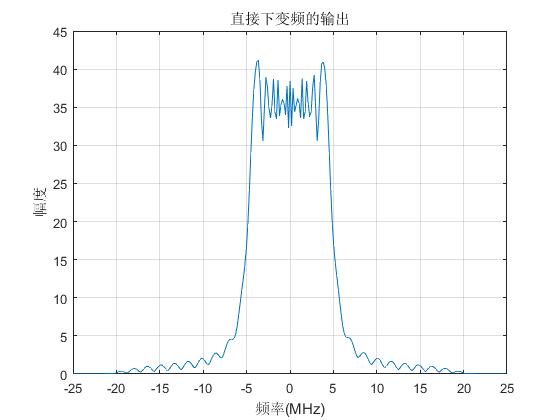
plot(f/1e6,abs(Yjw));grid;
title('直接下变频的输出');xlabel('频率(MHz)'),ylabel('幅度');
%===========================================================================================================================
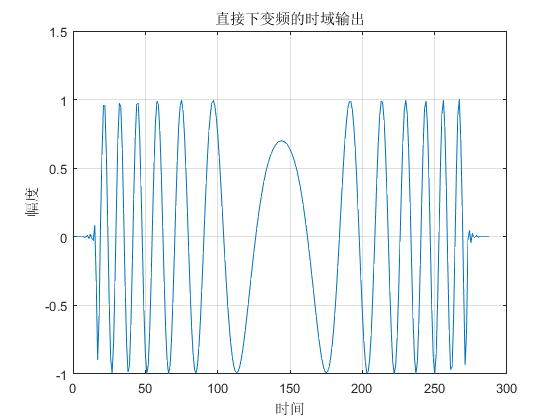
figure(50)
plot(real(Y2));grid;
title('直接下变频的时域输出');
xlabel('时间'),ylabel('幅度');
%===================================================================================================================
%% 得到多相滤波器
for r=1:16 %r=1
for k=1:8 %k=1
h(k,r)=b((r-1)*8+k); %h(1,1)=b(1);h(1,2)=b(2);..%将b的128个数放入16*8的矩阵里面,放完上一排再放下一排
end
end
%% 对信号进行抽取
for k=1:4
for r=1:256
S(k,r)=s((r-1)*4+k); %将s里1024个数横排放置后分成四排
end
s=shiftdim(s,-1); %shiftdim(A,1)使A的维号左移1位,就是第2维变第1维,第3维变第2维,第1维变最后维。
end
SS=circshift(S,[1,-1]); %循环移位 %B= circshift(A,K,m);如果同时对矩阵进行行和列的移位则令K= [col,row],其中col表示列位移,row表示行位移。
ss(1,:)=SS(2,:);
ss(2,:)=SS(3,:);
ss(3,:)=SS(4,:);
ss(4,:)=SS(1,:);
S=[S;ss];
for ii=1:8
if mod(ii,2)~=0
Ss(ii,:)=S(ii,:);
elseif mod(ii,2)==0
Ss(ii,:)=S(ii,:);
end
end
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 实现多相滤波的过程
for ii=1:8
yout=conv(h(ii,:),Ss(ii,:));
Yo(ii,:)=yout;
end
Yout1=fft(Yo,[],1);
Yout2=fftshift(Yout1);
Yout=fft(Yout2,[],2);
Yout=fftshift(Yout);
figure(6)
N3=length(Yout(1,:));
f=[-N3/2:N3/2]/N3*fs/4;f(end)=[];
plot(f/1e6,abs(Yout(1,:)));grid; title('第1信道输出'); xlabel('频率(MHz)'),ylabel('幅度');

%===========================================================================================================================
figure(7)
N3=length(Yout(2,:));
f=[-N3/2:N3/2]/N3*fs/4;f(end)=[];
plot(f/1e6,abs(Yout(2,:)));grid; title('第2信道输出'); xlabel('频率(MHz)'),ylabel('幅度');

%==============================================================================================================
figure(8)
N3=length(Yout(3,:));
f=[-N3/2:N3/2]/N3*fs/4;f(end)=[];
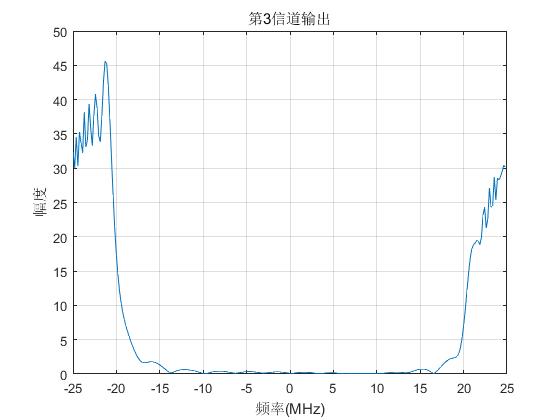
plot(f/1e6,abs(Yout(3,:)));grid; title('第3信道输出'); xlabel('频率(MHz)'),ylabel('幅度');
%================================================================================================================
figure(9)
N3=length(Yout(4,:));
f=[-N3/2:N3/2]/N3*fs/4;f(end)=[];
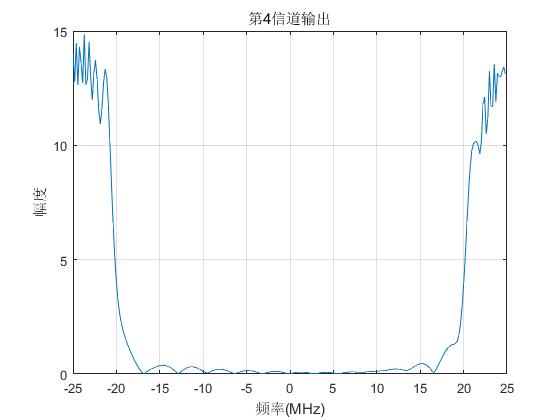
plot(f/1e6,abs(Yout(4,:)));grid; title('第4信道输出'); xlabel('频率(MHz)'),ylabel('幅度');
%=================================================================================================================
figure(10)
N3=length(Yout(5,:));
f=[-N3/2:N3/2]/N3*fs/4;f(end)=[];
plot(f/1e6,abs(Yout(5,:)));grid; title('第5信道输出'); xlabel('频率(MHz)'),ylabel('幅度');

%=============================================================================================================
figure(11)
N3=length(Yout(6,:));
f=[-N3/2:N3/2]/N3*fs/4;f(end)=[];
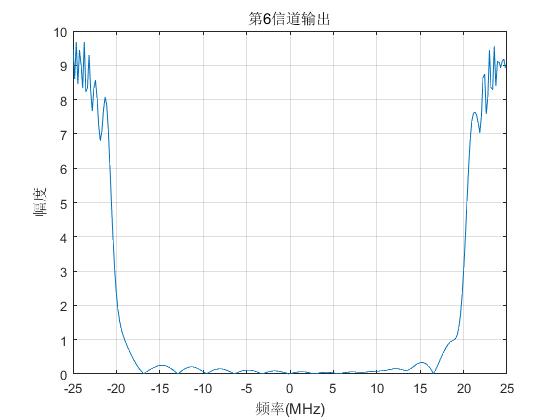
plot(f/1e6,abs(Yout(6,:)));grid; title('第6信道输出'); xlabel('频率(MHz)'),ylabel('幅度');
%===============================================================================================================
figure(12)
N3=length(Yout(7,:));
f=[-N3/2:N3/2]/N3*fs/4;f(end)=[];
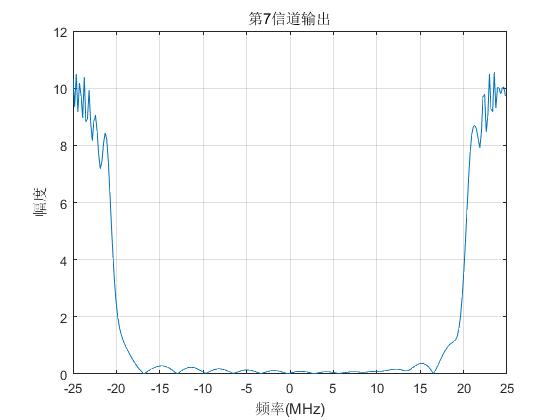
plot(f/1e6,abs(Yout(7,:)));grid; title('第7信道输出'); xlabel('频率(MHz)'),ylabel('幅度');
%=====================================================================================================================
figure(90)
plot(real(Yout1(7,:)));grid; title('多相滤波的时域输出'); xlabel('时间'),ylabel('幅度');

%=======================================================================================================================
figure(13)
N3=length(Yout(8,:));
f=[-N3/2:N3/2]/N3*fs/4;f(end)=[];
plot(f/1e6,abs(Yout(8,:)));grid; title('第8信道输出'); xlabel('频率(MHz)'),ylabel('幅度');

%=====================================================================================================================
命令说明:最佳FIR滤波器阶数估计
[n,fo,ao,w] = firpmord(f1,a1,dev1)
b = firpm(n,fo,ao,w);
freqz(b,1,1024,fs);
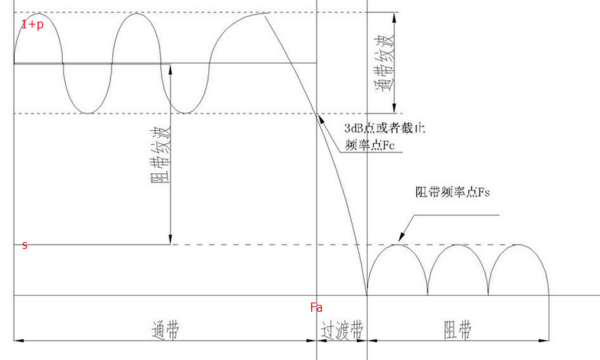
计算滤波器的阶数n
f1是设计滤波器频率边缘带的向量, 例如上述低通滤波器 就是截至频率和阻带开始频率。(最低阶低通滤波器通带截止频率是(a)Hz,阻带截止频率(b)Hz,f1=[a,b])
a是设计滤波器时的通带,阻带的幅度,一般都是向量。(在我看的例子里,是[1,0])
dev1是设计滤波器时,通带波动 p 和阻带衰减s所组成向量。(通带波纹小于(rp)dB,阻带衰减大于(rs)dB,dev = [(10^(rp/20)-1)/(10^(rp/20)+1) 10^(-rs/20)];)
如这个程序:
c = firpmord([1500 2000],[1 0],[0.01 0.1],8000,'cell');
B = firpm(c{:});
freqz(B,1,1024,8000)
得到的函数图像如下,把0.01和0.1分别化成db形式,就和图中的通带波动-1,阻带衰减相对应了。
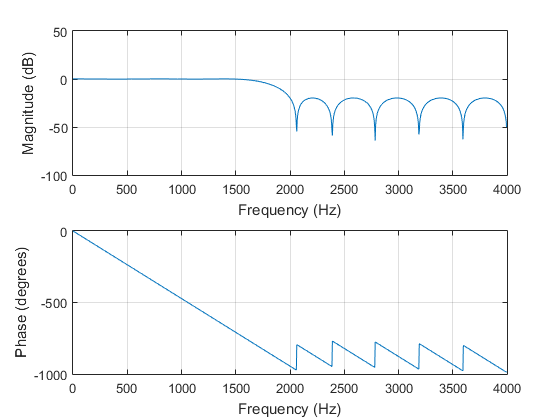
%==========================================================================================================================
在matlab中实现函数的抽样用法:
一、dyaddown
功能:对时间序列进行二元采样,每隔一个元素提取一个元素,得到一个降采样时间序列。 格式:
1.y = dyaddown(x, EVENODD)
当EVENODD=0时,从x中第二个元素开始采样(偶采样);当EVENODD=1时,从x中第一个元素开始采样(奇采样)。
2.y = dyaddown(x)
EVENODD缺省,按EVENODD=0
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
二、dyadup
功能:对时间序列进行二元插值,每隔一个元素插入一个0元素,得到一个时间序列。 格式:
1.y = dyadup(x, EVENODD)
当EVENODD=0时,从x中第二个元素开始采样(偶采样);当EVENODD=1时,从x中第一个元素开始采样(奇采样)。
2.y = dyadup(x)
EVENODD缺省,按EVENODD=0
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
三、interp
功能:对时间序列进行整数倍插值,使得时间序列曲线更光滑。 格式:
1.y = interp(x, r)
在x中插入一些数据,使得插值后的序列y的长度为x的r倍。
2.y = interp(x, r, l, alpha)
插值后得到的序列y的长度为x的r倍。
3.[y, b] = interp(x, r, l, alpha)
插值后同时得到一个低通插值滤波器的系数,长度为2rl+1. 说明: x--时间序列 r--插入点的倍数 l--插值滤波器长度
alpha--滤波器的截止频率,0<alpha<=1,假设原序列的采样频率之半为1,缺省时l=4,alpha=0.5.
y--插值后得到的时间学列
b--低通插值滤波器的系数,长度为2rl+1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
四、downsample
功能:对时间序列重采样,在原时间序列中等间隔地取出一些项,得到新序列。 格式:
1.y = downsample(x, n)
从第一项开始,等间隔n对x采样,得到的序列为y。
2.y = downsample(x, n, phase)
从第phase+1项开始,等间隔n对x采样,得到的序列为y,而0<=phase<n.
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
五、decimate
功能:对时间序列进行整数倍采样处理,使得时间序列的长度降低。 格式:
1.y = decimate(x, r)
将时间序列x的采样频率降低为原来的1/r,即length(y)=length(x)/r。在抽取之前,默认地采用了8阶chebyshevI型低通滤波器压缩频带。
2.y = decimate(x, r, n)
采用n阶chebyshevI型低通滤波器。
3.y = decimate(x, r, ‘fir’)
采用30阶的FIR型低通滤波器来压缩频带,对时间序列进行整数倍抽取。
4.y = decimate(x, r, n, ‘fir’)
指定当对时间序列进行整数倍抽取的时候,采用n点FIR型低通滤波器来压缩频带,对时间序列进行整数倍抽取。 说明: x--时间序列 r--采样要降低的倍数
n--指定所采用的chebyshevI型低通滤波器的阶数 ‘fir’--FIR滤波器
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
六、resample
功能:对时间序列进行重采样。 格式:
1.y = resample(x, p, q)
采用多相滤波器对时间序列进行重采样,得到的序列y的长度为原来的序列x的长度的p/q倍,p和q都为正整数。此时,默认地采用使用FIR方法设计的抗混叠的低通滤波器。
2.y = resample(x, p, q, n)
采用chebyshevIIR型低通滤波器对时间序列进行重采样,滤波器的长度与n成比例,n缺省值为10.
3.y = resample(x, p, q, n, beta)
beta为设置低通滤波器时使用Kaiser窗的参数,缺省值为5.
4.y = resample(x, p, q, b)
b为重采样过程中滤波器的系数向量。
5.[y, b] = resample(x, p, q)
输出参数b为所使用的滤波器的系数向量。 说明: x--时间序列
p、q--正整数,指定重采样的长度的倍数。
n--指定所采用的chebyshevIIR型低通滤波器的阶数,滤波器的长度与n成比列。 beta--设计低通滤波器时使用Kaiser窗的参数,缺省值为5。
%===========================================================================================================================
reshape,shiftdim,permute:
reshape后变为2行2列3层的三维矩阵。三维矩阵可以用3个下标定位,也可以用1个下标定位,定位时的顺序也是先第一个维度,再第二个维度,最后第三个维度。reshape前后不改变一维下标定位顺序,即A(1,1,1)=A(1)=data(1)=1,A(2,1,1)=A(2)=data(2)=5,A(1,2,1)=A(3)=data(3)=9,A(2,2,1)=A(4)=data(4)=2,A(1,1,2)=A(5)=data(5)=6,以此类推
shiftdim(A,1)使A的维号左移1位,就是第2维变第1维,第3维变第2维,第1维变最后维。A是2*2*3的矩阵,Adim就是2*3*2的矩阵,并且有A(1,2,3)=Adim(2,3,1),A(1,2,1)=Adim(2,1,1),以此类推
permute(A,[2,3,1])使A的维号按照先第2维、再第3维,最后第1维的顺序排列。在这里得到的矩阵和Adim完全相同。permute的功能比shiftdim强大,可以实现维号的任意顺序排列(或称置换),而shiftdim只是permute按左移(或右移)排列(数学上称为轮换)的一个特例。
%=========================================================================================================
参考:
多相滤波:https://wenku.baidu.com/view/fbb8280f83c4bb4cf7ecd156?from=singlemessage
滤波器参考:https://wenku.baidu.com/view/43228000de80d4d8d15a4f71.html
circshift: https://blog.csdn.net/xuexiopencv/article/details/51202794