求组合数

从m个不同元素中，任取n(n≤m)个元素并成一组，叫做从m个不同元素中取出n个元素的一个组合；

从m个不同元素中取出n(n≤m)个元素的所有组合的个数，叫做从m个不同元素中取出n个元素的组合数。

 combinatorial number

  /     

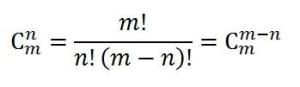
在线性写法中被写作C(m,n)。

c(m,n)=p(m,n)/n!=m!/((m-n)!*n!)

 组合数的计算：C(n,k)有多种解法，1，dp递推；2，直接计算；3，lucas定理

性质：

性质1 C(n,m)= C(n,n-m)互补性质

　　例如C(9,2)=C(9,7)，即从9个元素里选择2个元素的方法与从9个元素里选择7个元素的方法是相等的。

　　规定：C(m,0)=1

性质2 C(n,m)=  C(n-1,m-1)+C(n-1,m) 组合恒等式

摘自http://blog.csdn.net/wty__/article/details/20048467

1.最简单的情况，数据比较小，直接采用C(a, b) = a * (a - 1) *....* (a - b + 1) / (b * (b - 1) *...* 2 * 1)
试用数据范围：a <= 29。在a = 30, b = 15时，计算分子乘积时即超范围

补救1.是将先乘后除改为交叉地进行乘除，先除能整除的，但也只能满足n稍微增大的情况，n最多只能满足两位数。

补救2.是换用高精度运算，这样结果不会有问题，只是需要实现大数相乘、相除和取模等运算，实现起来比较麻烦，时间复杂度为O(n)。

LL combi(LL a,LL b)///从a中取b
{
    if(a<b){
        return 0;
    }
    LL r=1;
    for(int i=a;i>=a-b+1;i--)
        r*=i;
    for(int j=b;j>1;j--)
        r/=j;
    return r;
}

2.预处理（打表）出需要的组合数，如需计算较大的组合数可采用（经常会取模，也很方便）。使用C(a, b) = C(a - 1, b - 1) + C(a - 1, b - 1)递推处理
因为计算过程中采用递推的加法运算，所以不取模的时候最大可以算到a = 66
但是，这种情况一般伴随着取模的操作，所以考虑到内存限制的时候，一般可以计算到a = 1000（不一定，受限于内存）

生成的复杂度为O(n^2)，查询复杂度为O(1)。

算法的预处理时间较长，另外空间花费较大，都是平方级的，优点是实现简单，查询时间快。

const int MAXN1 = 1000;  
const int MAXN2 = 1000;  
LL f[MAXN1][MAXN2];  
  
void init()  
{  
    FF(i, 0, MAXN1)  
        f[i][0] = 1;  
    FF(i, 1, MAXN1)  
    {  
        FE(j, 1, min(i, MAXN2 - 1))  
            f[i][j] = (f[i - 1][j] + f[i - 1][j - 1]) % MOD;  
    }  
}  

3.质因数分解：

采用分解质因子的方式，可以计算足够大的数（因为数字会超过long long的范围，所以结果依然用质因子表示，模板中计算出了相应的数）

设n!分解因式后，质因数p的次数为a；对应地m!分解后p的次数为b；(n-m)!分解后p的次数为c；则C(n,m)分解后，p的次数为a-b-c。计算出所有质因子的次数，它们的积即为答案，即C(n,m)=p1 a1-b1-c1p2 a2-b2-c2…pk ak-bk-ck。n!分解后p的次数为：n/p+n/p 2+…+n/p k。算法的时间复杂度比前两种方案都低，基本上跟n以内的素数个数呈线性关系，而素数个数通常比n都小几个数量级，例如100万以内的素数不到8万个。用筛法生成素数的时间接近线性。该方案1秒钟能计算 1kw数量级的组合数。如果要计算更大，内存和时间消耗都比较大。https://segmentfault.com/a/1190000005072018#articleHeader0

#include <iostream>
#include "cstdio"
#include "map"
#include "cmath"
using namespace std;
#define LL long long
map <int, LL> m;

///分解质因数
///k为1或-1
void fun(int n, int k)
{
    for (int i = 2; i <= sqrt(n * 1.0); i++)
    {
        while (n % i == 0)
        {
            n /= i;
            m[i] += k;///存储因数+次数（k=-1倒数）
        }
    }
    if (n > 1)
    {
        m[n] += k;
    }
}

///快速幂
LL quick_pow(LL a, LL b)
{

    LL ret = 1;
    while (b)
    {
        if (b & 1)
        {
            ret *= a;
        }
        b >>= 1;
        a *= a;
    }
    return ret;
}

///求组合数
LL C(LL a, LL b)
{
    if (a < b || a < 0 || b < 0)
        return 0;
    m.clear();
    LL ret = 1;
    b = min(a - b, b);
    for (int i = 0; i < b; i++)
    {
        fun(a - i, 1);///分母
    }
    for (int i = b; i >= 1; i--)
    {
        fun(i, -1);///分子
    }

    ///以下计算出了具体的数
    for (__typeof(m.begin()) it = m.begin(); it != m.end(); it++)
    {
        if ((*it).second != 0)
        {
            ret *= quick_pow((*it).first, (*it).second);///快速幂，在之前分解质因数时 在过程+（-1）中其实已经运算了一部分，所以才不容易乘过界。
        }
    }
    return ret;
}
int main()
{
    LL a,b;
    while(~scanf("%lld%lld",&a,&b)&&a&&b)
    {
        cout<<C(a,b)<<endl;
    }
}

Lucas定理，设p是一个素数（题目中要求取模的数也是素数），将n,m均转化为p进制数，表示如下：

满足下式：

即C(n,m)模p等于p进制数上各位的C(ni,mi)模p的乘积。利用该定理，可以将计算较大的C(n,m)转化成计算各个较小的C(ni,mi)。该方案能支持整型范围内所有数的组合数计算，甚至支持64位整数，注意中途溢出处理。该算法的时间复杂度跟n几乎不相关了，可以认为算法复杂度在常数和对数之间。

#include <stdio.h>
const int M = 10007;
int ff[M+5];  //打表，记录n!，避免重复计算

//求最大公因数
int gcd(int a,int b)
{
    if(b==0)
return a;
else
return gcd(b,a%b);
}

//解线性同余方程，扩展欧几里德定理
int x,y;
void Extended_gcd(int a,int b)
{
    if(b==0)
    {
       x=1;
       y=0;
    }
    else
    {
       Extended_gcd(b,a%b);
       long t=x;
       x=y;
       y=t-(a/b)*y;
    }
}

//计算不大的C(n,m)
int C(int a,int b)
{
    if(b>a)
return 0;
    b=(ff[a-b]*ff[b])%M;
    a=ff[a];
    int c=gcd(a,b);
    a/=c;
    b/=c;
    Extended_gcd(b,M);
    x=(x+M)%M;
    x=(x*a)%M;
    return x;
}

//Lucas定理
int Combination(int n, int m)
{
        int ans=1;
int a,b;
while(m||n)
{
        a=n%M;
b=m%M;
n/=M;
m/=M;
ans=(ans*C(a,b))%M;
}
return ans;
}

int main(void)
{
        int i,m,n;
ff[0]=1;
for(i=1;i<=M;i++)  //预计算n!
ff[i]=(ff[i-1]*i)%M;
 
scanf("%d%d",&n, &m);
printf("%d
",func(n,m));
 
return 0;
}