| 时限:5000 MS | 内存限制:65536K | |
| 提交材料共计: 6204 | 接受: 2563 |
描述
相应的图片如下:

图1
如果一些相邻的盒子都是相同的颜色,并且它左边的盒子(如果它存在)和它的右边的盒子(如果它存在)都是其他颜色的,我们称它为“盒子段”。有四个盒子段。那就是:金,银,铜,金。片段中分别有1,4,3,1方框。
每次您可以单击一个框,然后包含该框的整个段消失。如果这段是由k个方框组成的,你会得到k*k点。例如,如果你点击一个银盒子,银段消失了,你得到4*4=16点。
现在让我们看看下面的图片:
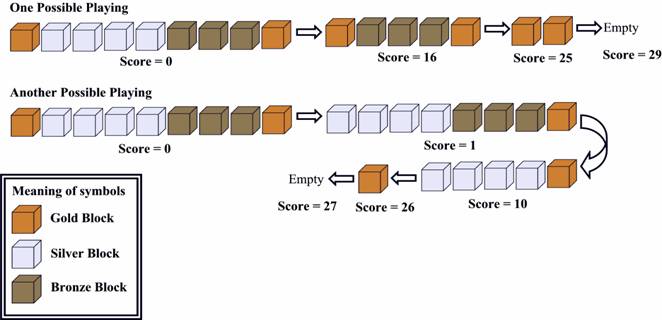
图2
第一个是最优的。
在这个游戏的初始状态下,找出你能得到的最高分数。
输入
输出量
样本输入
2 9 1 2 2 2 2 3 3 3 1 1 1
样本输出
Case 1: 29 Case 2: 1
解题思路:
将连续的若干个方块作为一个“大块”(box_segment) 考虑,假设开始一共有 n个“大块”,编号0到n-1 第i个大块的颜色是 color[i],包含的方块数目,即长度,是len[i]
用click_box(i,j)表示从大块i到大块j这一段消除后所能 得到的最高分,则整个问题就是: click_box(0,n-1)。
要求click_box(i,j)时,考虑最右边的大块j,对它有两种处理方式,要取其优者:
1) 直接消除它,此时能得到最高分就是: click_box(i,j-1) + len[j]*len[j]
2) 期待以后它能和左边的某个同色大块合并,考虑和左边的某个同色大块合并:
左边的同色大块可能有很多个,到底和哪个合并最 好,不知道,只能枚举。假设大块j和左边的大块 k(i<=k<j-1) 合并,此时能得到的最高分是多少呢?
是不是: click_box(i,k-1) + click_box(k+1,j-1) + (len[k]+len[j])
不对! 因为将大块k和大块j合并后,形成的新大块会在最右边。但直接将其消去,未必是最好的,也许它还应该和左边的同色大块合并,才更好
那么上面的dp不可用,需要改变问题的形式
__________________________________________________________________
click_box(i,j,ex_len) 表示: 大块 j 的右边已经有一个长度为ex_len的大块(该大块可能是在合并过程中形成的),且 j 的颜色和ex_len相同,在此情况下所能得到的最高分 。
于是整个问题就是求:click_box(0,n-1,0)
求click_box(i,j,ex_len)时,有两种处理方法取最优者,假设j和ex_len合并后的大块称作 Q
1) 将Q直接消除,这种做法能得到的最高分就是: click_box(i,j-1,0) + (len[j]+ex_len)2
2) 期待Q以后能和左边的某个同色大块合并。需要枚举可能和Q 合并的大块。假设让大块k和Q合并,则此时能得到的最大分数是:
click_box(i,k,len[j]+ex_len) + click_box(k+1,j-1,0)
click_box(i,j,ex_len) 递归的终止条件: i == j
代码:
#include<iostream> #include<cstring> using namespace std; #define N 200 + 5 int dp[N][N][N]; struct segMent { int len; int color; }; segMent segNum[N]; int clickBox(int i, int j, int len) { if(dp[i][j][len] != -1) return dp[i][j][len]; int result = (segNum[j].len + len)*(segNum[j].len + len); if(i == j) return result; result += clickBox(i, j-1, 0); for(int k = i; k < j; k++) { if(segNum[k].color != segNum[j].color) continue; int r = clickBox(k+1, j-1, 0) + clickBox(i, k, segNum[j].len + len); result = max(result, r); } dp[i][j][len] = result; return result; } int main() { int T; cin >> T; for(int t = 1; t <= T; t++) { int n; cin >> n; int last = -1; int count = -1; memset(dp, -1, sizeof(dp)); for(int i = 0; i < n; i++) { int v; cin >> v; if(v != last) { count++; segNum[count].len = 1; segNum[count].color = v; last = v; } else segNum[count].len++; } cout << "Case " << t << ": " << clickBox(0, count, 0) << endl; } return 0; }