在阅读LIFT:Learned Invariant Feature Transform一文时,文中第1节提到为了保证端到端的可微性,利用softargmax来代替传统的NMS(非极大值抑制)来挑选极值点位置。由于只了解softmax,对于softargmax不甚了解,所以记录下来。
1)softmax:
输入为向量,输出为值为0-1之间的向量,和为1。在分类任务中作为概率出现在交叉熵损失函数中。
import numpy as np
data=np.array([0.1, 0.3, 0.6, 2.1 ,0.55])
np.exp(data)/np.sum(np.exp(data)) # softmax
array([ 0.07795756, 0.09521758, 0.12853029, 0.57603278, 0.12226179])
2)argmax:为了得到一个向量中最大值所处的位置,我们利用此函数。但是这个函数不可导,所以无法计算其梯度。然而我们可以利用软化的max函数来计算,就是softmax。利用softmax,我们可以得到每个元素正则化后的值。此向量()分布)的
此时最大值所处的坐标期望即为:![]()
np.sum(np.exp(data)/np.sum(np.exp(data)) * np.array([0,1,2,3,4])) # E = p*index
2.5694236670240085。而最大之所在的位置应该是3。
3)softargmax:从上面看到位置计算不够准确,一个原因就是最大值的概率不够大,或者说增大相对最大值而减弱其他值的影响就可以得到更加准确的位置坐标。
softargmax: 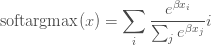
可以看到,上式与softmax的期望只有一个差别,即给向量的每个元素乘以beta。
>>>d = data*10 # beta=10
array([ 1. , 3. , 6. , 21. , 5.5])
>>> np.sum(np.exp(d)/np.sum(np.exp(d)) *np.array([0,1,2,3,4]))
2.9999998429934758
可见此时输出的坐标为2.99,即为3,且这种寻找极值所在位置(坐标)的方法是可微的。常用于图像特征点位置的提取。
此外,LIFT原文3.5节提到:softargmax作为非极大值抑制NMS的可微分版本。就是说可以利用softargmax来替代NMS。
Ref: