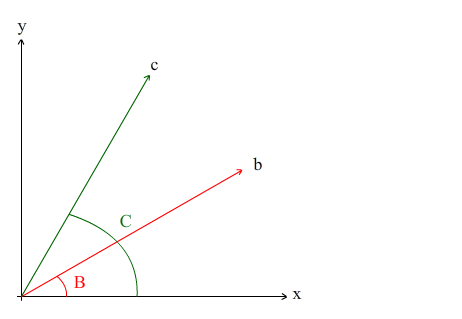
点积最重要的应用是计算两个向量的夹角,或者两条直线的夹角。图给出了二维的情况,其中向量b和向量c与x轴的夹角分别为B,C,从基本三角函数可得:
b = (|b| cosB, |b| sinB) //|b|表示b的模就是b的长度
c = (|c| cosC, |c| sinC)
将上式代入点积等式,将它们的对应的分量相乘,再把结果相加,于是得到:
b•c = |b| |c| cosB cosC + |b| |c| sinB sinC
再次应用三角函数等式,得到
b•c = |b| |c| cos(B-C)
最终,对于任意两个向量b和c,我们有
b•c = |b| |c| cos(@),即cos(@) = b•c / (|b| |c|)
注:@为b和c之间的夹角。