论文笔记SPP_NET中提到的金字塔

      时隔这么久终于考完试放假了，现在终于有时间开始研究spp net的相关内容了，看了几篇网上的博客，发现看完之后还是不是很懂，于是乎下载了spp net的原始论文《Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recongnition》开始，由于中间的关键思想来自于Spatial Pyramid Matching（我把它翻译成“空间金字塔匹配”），而“空间金字塔匹配”的思想又来自于Pyramid Match Kernel（金字塔匹配核），本着反正我是图像处理初学者，多写点可以以后做论文的想法，我决定慢慢的看这几篇文章

• Pyramid Match Kernel（金字塔匹配核）

1. 预备知识

    《The Pyramid Match Kernel:Discriminative Classification with Sets of Image Features》是提出空间金字塔的那篇文章中指明所引用的是这篇文章，在我下载了这篇文章看了前半段后，我发现我在这个方法的第一步，利用特征空间里的特征向量来构建一个多分辨率的特征直方图我都看不懂作者是如何操作的，于是乎在网上找了很久的资料，发现了一篇07年的文章《The Pyramid Match Kernel: Efficient Learning with Sets of Features》，这俩篇论文的作者是同一个人，第二篇比第一篇讲的更加的详细一些，虽然还是有些疑问，但是加上自己的脑补和网上的资料，似乎有点点能看懂了。

      假设我们有个特征描述子能够使用d维的向量来描述一些点的特征，d维特征向量的空间称为F，如sift特征（使用128维的特征向量来描述一个特征点），对于一副图片，我们能检测出m个特征点，每个特征点都用一个d维的特征向量来表示，把这些向量放在一个集合X中，X={(x₁,x₂,x₃,...x_d)₁，(x₁,x₂,x₃,...x_d)_2，...(x₁,x₂,x₃,...x_d)_m},则这个向量集x就可以表示一个物体，作为匹配的输入的一系列图片的特征集就构成了输入空间S，S={X|X={x₁,x₂,x₃...x_m}},对于不同的实例，d的大小是固定的，m的大小确实不固定的，这就是金字塔匹配核的好处之一。用D表示特征空间F中每个向量中每一列属性的范围的最大值，将特征向量的数据缩放并强制转化为整型，来保证向量间的最小距离为1

      对于两个点集，局部匹配就是将数量较小的点集中的点映射到数量较大的点集中的点，例如对于两个点集X,Y，m=|X|,n=|Y|，m<=n,用数组      来表示X中点再Y中的对应点，所以匹配函数就可以记为M，相应的代价函数（也就是对应点之间的不匹配度的度量函数）记为C：

      要求得最佳的对应点，就是最小化这个代价函数，得到相应的：

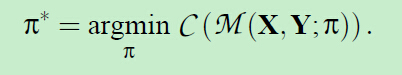
     相应的相似度计算就可以用类似于代价函数的方式进行定义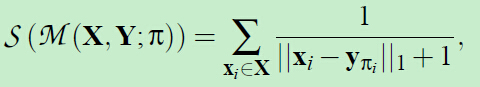：     分母加1是为了防止分母为0。

     2. 金字塔匹配算法

     金字塔匹配算法就是将一个特征空间中的向量映射到一个多维的，多分辨率的直方图集合中，多维是指直方图的列数是多个的，多分辨率是指这些直方图的每一列的宽度是变化的，从第一个到最后一个逐渐变大。第一层的直方图bin足够小，特征空间中的每一个向量都能单独放到一列中，分辨率最高，后面每一层的直方图的bin是前一个直方图bin的两倍，最后一层的直方图的bin大到可以将整个特征空间中的向量都容纳进去。将两个特征点集合中的点按照直方图所表示的范围顺序放入直方图中，在第一层直方图中可能两个集合中的点都是分散在直方图的各个列中，随着直方图的bin的加宽，两个集合中的特征点逐渐开始被分到同一个bin中，这时我们就认为他们匹配了。匹配的分数不用再像以前那样计算两个点之间的距离，两个点匹配时的直方图的bin的宽度就是这个bin中所容纳点的距离的最大值。具体操作时将每一个特征集都映射到一个多分辨率的直方图中，然后对每个直方图金字塔使用权重直方图交叉的方法进行比较。

     对于一个特征集X的特征提取方法记为：

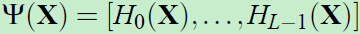
这里X∈S,L=log₂D+1(向上取整)，

--------------------------------------------------------------华丽丽的分割线------------------------------------------------------------------------------------------------------------------------------------------

为啥突然不看空间金字塔匹配算法了呢。。。因为当我把SPP-NET的论文看完后发现，人家原作者只是从金字塔那里获得了灵感，却没有真的完全运用金字塔的那套原理来实现spp-net，也就是说，没必要去完完整整的看空间金字塔的内容就可以很好的理解SPP-NET了。