扫描线求矩形面积并，使用线段树维护（感觉非常详细）

HDOJ1542 Atlantis

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1542

题意：求平面中矩形面积并。

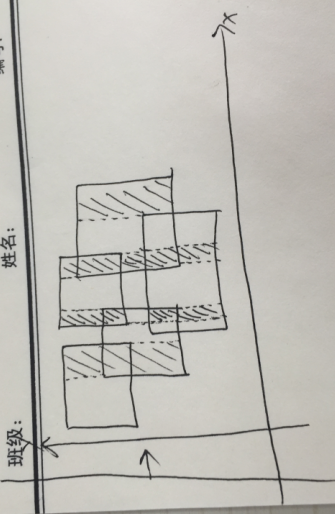
这张图阴影和空白交替标出了并的面积。

我是习惯从下向上扫描的。

根据之前的一道CF EducationalRound的题，可以知道Ox坐标下扫描线的基本思路：

“入”和“出”分别用-1和1来代替（但是这里需要在线段树中记录区间内边的条数，所以我把-1和1调换了位置，并且在cmp函数里修改了这个比较）

但是平面的话，想记录每一列的宽度情况，所以可以用线段树来维护：线段树中的区间[l,r]代表[l,r]这个大区间有多长的子区间是被覆盖的。当然首先要离散化，不过存储这个覆盖的长度仍然是未离散化的长度。

那么就会有类似于线段树中“区间合并”的问题了，但是这题很特殊，不需要区间合并。

特殊在哪里？

一般的区间合并希望查询特定的[l,r]区间内被覆盖的子区间的总长度，但是这里不需要查询特定的[l,r]区间，而是整棵线段树描述的区间的覆盖总长度。

所以我们很轻易地想到，在update到一个需要覆盖的子区间的时候，向上传递这个子区间的长度。

还会有一个问题：假如我在线段树上更新了一个表示区间[l,r]的节点rt，这个区间的父亲RT（假如表示区间[L, R]，其中L<=l, r<=R）有没有可能被覆盖呢？

这里就需要分情况讨论一下：

1：RT表示的区间已经被完全覆盖过了

2：RT表示的区间并没有被覆盖过，或者被覆盖了一部分

对于情况1：

很好理解。在这个大区间下，由加了一条包含在[L,R]里的线段，类似这样：

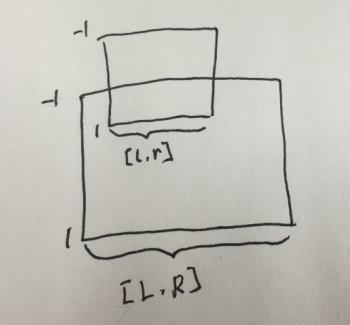
那我还需要使用[l,r]更新[L,R]的答案吗？很明显不需要。只需要用[L,R]代表的未离散化的长度更新一下当前值就行了。

问题：为什么不用[l,r]更新[L,R]，但是还要用未离散化的长度更新一下当前值？

因为pushup操作不只是发生在发现小区间，还要在某区间的左右儿子均更新结束后，向上传第一次。

对于情况2：

假如RT还没有覆盖过，或者覆盖了一部分：

显然RT的覆盖部分是从左右儿子代表的子区间更新来的，那么直接用左右儿子的覆盖区间长度和更新就行。

但是，假如RT代表的覆盖区间是一个点，即叶子的时候。显然一个点的区间长度是0，这点要注意特判一下。

这样就没有问题了，顺便，感觉自己的离散化姿势很好。

#include <bits/stdc++.h>
using namespace std;

#define lrt rt << 1
#define rrt rt << 1 | 1
const int maxn = 210;
typedef struct Seg {
    double len;
    int cnt;
}Seg;
typedef struct Event {
    double l, r, h;
    int sign;
}Event;

int n, hcnt;
double h[maxn];
vector<Event> event;
Seg seg[maxn<<2];

bool cmp(Event a, Event b) {
    if(a.h != b.h) return a.h < b.h;
    return a.sign > b.sign;
}

int id(double v) {
    return lower_bound(h, h+hcnt, v) - h + 1;
}

void build(int l, int r, int rt) {
    if(l == r) return;
    seg[rt].len = .0, seg[rt].cnt = 0;
    int mid = (l + r) >> 1;
    build(l, mid, lrt);
    build(mid+1, r, rrt);
}

void pushup(int l, int r, int rt) {
    if(seg[rt].cnt) seg[rt].len = h[r] - h[l-1];
    else {
        if(l == r) seg[rt].len = 0;
        else seg[rt].len = seg[lrt].len + seg[rrt].len;
    }
}

void update(int L, int R, int sign, int l, int r, int rt) {
    if(L <= l && r <= R) {
        seg[rt].cnt += sign;
        pushup(l, r, rt);
        return;
    }
    int mid = (l + r) >> 1;
    if(L <= mid) update(L, R, sign, l, mid, lrt);
    if(mid < R) update(L, R, sign, mid+1, r, rrt);
    pushup(l, r, rt);
}

int main() {
    // freopen("in", "r", stdin);
    int _ = 1;
    double ax, ay, bx, by;
    while(~scanf("%d", &n) && n) {
        event.clear(); hcnt = 0;
        for(int i = 0; i < n; i++) {
            scanf("%lf%lf%lf%lf",&ax,&ay,&bx,&by);
            event.push_back(Event{ax, bx, ay, 1});
            event.push_back(Event{ax, bx, by, -1});
            h[hcnt++] = ax; h[hcnt++] = bx;
        }
        sort(event.begin(), event.end(), cmp);
        sort(h, h+hcnt); hcnt = unique(h, h+hcnt) - h;
        build(1, hcnt, 1);
        double ret = .0;
        for(int i = 0; i < event.size(); i++) {
            int l = id(event[i].l);
            int r = id(event[i].r) - 1;
            int sign = event[i].sign;
            update(l, r, sign, 1, hcnt, 1);
            cout << event[i+1].h - event[i].h << endl;
            ret += (event[i+1].h - event[i].h) * seg[1].len;
        }
        printf("Test case #%d
", _++);
        printf("Total explored area: %.2f

", ret);
    }
    return 0;
}