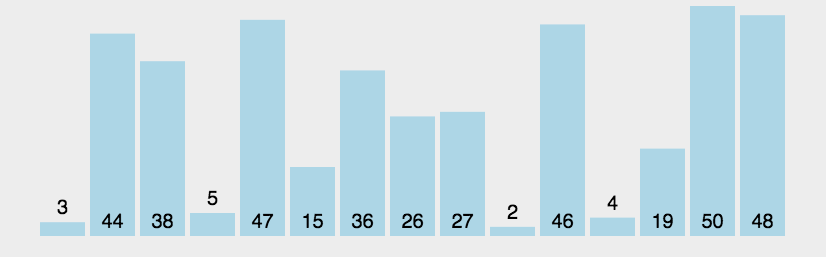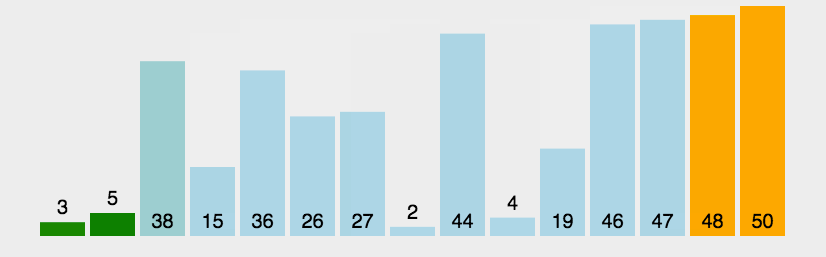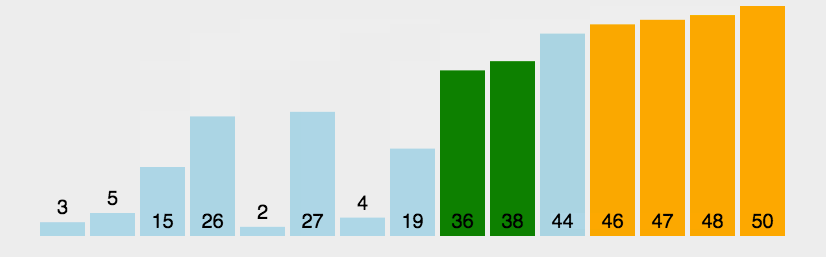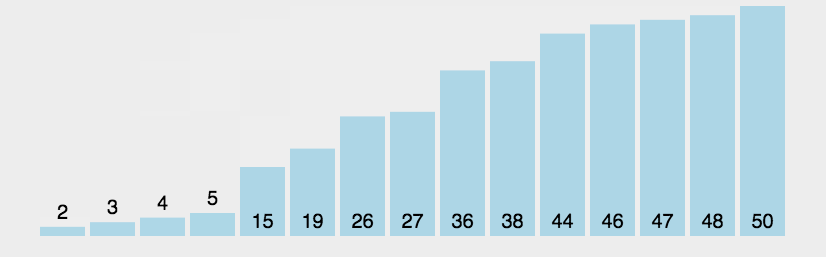主要排序算法(Python实现)

1. 冒泡排序

　　算法描述：1. 比较相邻的两个数，对升序(/降序)而言，若当前数小于(大于)后一个数则交换两者的位置。

　　　　　　　2.那么循环长度为L的列表，从第一个元素到倒数第(L-1)元素进行第1步操作，其结果是第L个元素必定是最小值；也就是说单次循环确定了一个数的排序位置，单次循环次数为(L-1)；

　　　　　　　3. 要确定所有元素的排序位置，还需要L-1次，因为每次循环确定了一个元素的位置，当第(L-1)次循环时，L-1个元素的位置都被确定了，剩下的一个自然被确定。

　　图片演示：

　　

 　　代码实现：

# coding:utf-8
import timeit

def bubble_sort(seq:list):
    """冒泡排序, seq为有效待排序列表"""
    for i in range(len(seq)-1):
        for j in range(len(seq)-1):
            if seq[j] < seq[j+1]:
                seq[j], seq[j+1] = seq[j+1], seq[j]
    return seq

if __name__ == '__main__':
    print(bubble_sort([i for i in range(10)]))
    # t = timeit.Timer("bubble_sort([i for i in range(1000)])", "from __main__ import bubble_sort")
    # print(t.timeit())

　　运行结果：

　　

　　最优时间复杂度：O(N)

　　最坏时间复杂度：O(N^2)

　　稳定性：稳定

2. 选择排序

　　算法描述：1. 将当前元素与其后所有元素进行比较，若大于(小于)则置换两个元素；

　　　　　　　2. 对于长度为L的列表，第1步操作完成能确定一个元素的位置；

　　　　　　　3.要确定L个元素的位置，则需循环L-1次；

　　图片演示：

　　

　　代码实现：

# coding:utf-8

def select_sort(seq:list):
    """选择排序(降序)"""
    for i in range(len(seq)-1):
        # 暂存待置换的元素的值
        cur_max = seq[i]
        for j in range(i+1, len(seq)):
            if seq[j] > cur_max:
                cur_max = seq[j]
                seq[i], seq[j] = seq[j], seq[i]
    return seq

if __name__ == '__main__':
    print(select_sort([i for i in range(10)]))　　

　　最优时间复杂度：O(N^2)

　　最坏时间复杂度：O(N^2)

　　稳定性：不稳定

3. 插入排序

　　算法描述：选择排序的关键在于向后比较，而插入排序与之相反，是向前比较并调整相应元素位置；

　　　　　　　1. 对于列表长度为L的列表而言，循环从第N个数开始向前与第N-1进行比较，若大于(小于)则交换位置；

　　　　　　　2. 要实现所有的数排序，另加一层L-1次的循环；

　　图片演示：

　　

　　代码实现：

# coding:utf-8

def insert_sort(seq:list):
    """插入排序(降序)"""
    for i in range(len(seq)):
        for j in range(i, 0, -1):
            # 倒序交换相邻两个的取值
            if seq[j] > seq[j-1]:
                seq[j], seq[j-1] = seq[j-1], seq[j]
    return seq

if __name__ == '__main__':
    print(insert_sort([i for i in range(10)]))

　　最优时间复杂度：O(N)

　　最坏时间复杂度：O(N^2)

　　稳定性：稳定

4. 快速排序

　　算法描述：　　　　　　　

　　一趟快速排序的算法是：

　　1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；

　　2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；

　　3）从j开始向前搜索，即由后开始向前搜索(j--)，找到第一个小于key的值A[j]，将A[j]和A[i]的值交换；

　　4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]的值交换；

　　5）重复第3、4步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）。

　　图片演示：

　　

　　

　　代码实现：

# coding:utf-8

def fast_sort(seq:list, left, right):
    """
    快速排序(升序)
    :param left:左部起始位置
    :param right: 右部起始位置
    """
    if right<=left:
        return

    low = left
    high = right

    # 基准值
    mid = seq[left]

    while low < high:
        # 从右扫描找出小于基准值的数
        while low<high and seq[high]>mid:
            high -= 1
        seq[low] = seq[high]
        # 向左扫描找出大于基准值的数
        while low<high and seq[low]<=mid:
            low += 1
        seq[high] = seq[low]

    # 此时low=high, 确定了基准值在序列中的排序位置
    seq[low] = mid

    # 递归排序low左右两边的序列
    fast_sort(seq, low+1, right)
    fast_sort(seq, left, low-1)


if __name__ == '__main__':
    seq = [i for i in range(10,0,-1)]
    fast_sort(seq, 0, len(seq)-1)
    print(seq)

　　最优时间复杂度：O(NlogN)

　　最坏时间复杂度：O(N^2)

　　稳定性：不稳定

5. 希尔排序

　　算法描述：

　　　　　　希尔排序是对插入排序的一种优化，主要在于设置了以步长来比较两个元素的值；

　　　　　　1. 

　　图片演示：

 

　　代码实现：

　　

　　最优时间复杂度：O(NlogN)

　　最坏时间复杂度：O(N^2)

　　稳定性：不稳定