求用1 * 2的骨牌覆盖n * m的矩形的方案数\(,2\leq n\leq 5,m\leq 10^9\)。
n很小,考虑状压,我们用一个集合s表示某一列中每个格子是否被覆盖,每列有n个格子,所以这样的集合有\(2^n\)种。
定义状态\(F(i,s)\)表示当第i列为s时的方案数。
对于第i列一个确定的状态s,我们可以通过将第i列填满从而到达第i+1列的某个状态。比如:
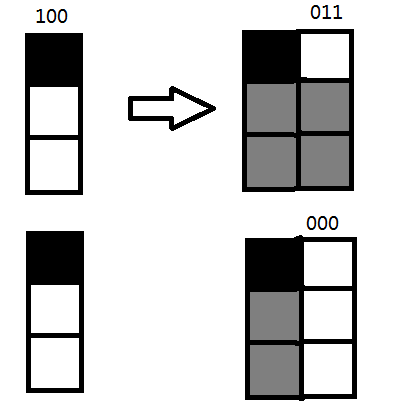
对于每个s可以用暴搜搜出来s可以转移到什么状态,以及转移到某种状态的方案数。这部分的复杂度是远低于\(O(2^{2n})\)的。
于是我们得到了一个大小为\(2^n*2^n\)的转移矩阵,第i+1列只跟第i列有关,用矩阵快速幂优化即可,复杂度\(O(4^n+2^{3n}*\log m)\)。
code
#include<stdio.h>
typedef long long LL;
const int mod=1000000007;
inline int Mod1(int x){return x>=mod?x-mod:x;}
int m,n,N,ss;
int F[32][32],Q[32][32],T[32],G[32];
void Dfs(int u,int s,int t){
if(u==n){
F[ss][t]++;
return;
}
if(s&(1<<u)){
Dfs(u+1,s,t);
return;
}
t|=(1<<u); s|=(1<<u);
Dfs(u+1,s,t);
t^=(1<<u); s^=(1<<u);
if(u+1<n&&((s&(1<<(u+1)))==0)){
s|=(1<<u); s|=(1<<(u+1));
Dfs(u+1,s,t);
s^=(1<<u); s^=(1<<(u+1));
}
}
void Init(){
N=(1<<n);
for(int s=0;s<N;++s){
ss=s;
Dfs(0,s,0);
}
T[0]=1;
while(m){
if(m&1){
for(int j=0;j<N;++j){
int x=0;
for(int k=0;k<N;++k){
x=Mod1(x+(LL)T[k]*F[k][j]%mod);
}
G[j]=x;
}
for(int j=0;j<N;++j) T[j]=G[j];
}
m>>=1;
for(int i=0;i<N;++i){
for(int j=0;j<N;++j){
int x=0;
for(int k=0;k<N;++k){
x=Mod1(x+(LL)F[i][k]*F[k][j]%mod);
}
Q[i][j]=x;
}
}
for(int i=0;i<N;++i) for(int j=0;j<N;++j) F[i][j]=Q[i][j];
}
printf("%d\n",T[0]);
}
int main(){
scanf("%d%d",&m,&n);
Init();
return 0;
}