斯坦福2014机器学习笔记六----神经网络(二)

一、纲要

　　神经网络代价函数

　　反向传播(BackPropagation)算法

　　梯度检验

　　参数随机初始化

　　总结

二、内容详述

　　1、神经网络代价函数

　　在逻辑回归中，我们的输出只有一个变量，是标量，就是一个y，但是在神经网络中我们可以有K个输出量，所以神经网络中的输出y是个K*1的向量，所以这里需要在逻辑回归的代价函数的基础上进行修改，修改后的代价函数如下：

这里k=1：K的意思是表示第1个输出量到第K个输出量，同时正则化项也进行了调整，逻辑回归中的参数θ是列向量n*1维，神经网络中的参数θ是矩阵，尺寸为(S_j+1 * S_j+1)，L表示第L层，那么这里θ的上下标表示的意思也就明白了。注意的另外一点是，跟逻辑回归一样，并不把θ_j0加进去，而是需要单独考虑。

　　2、反向传播算法

　　之前我们在计算神经网络预测结果的时候用了前向传播算法，即从input layer开始一层层计算到output layer。这里为了计算代价函数J(θ)的偏导数，我们采用一种反向传播算法。首先我们定义一个误差值ξ，ξ_j⁽ⁱ⁾表示第i层的第j个单元的激励值的误差，ξ_j⁽ⁱ⁾=a_j⁽ⁱ⁾-y⁽ⁱ⁾，这里的y⁽ⁱ⁾为训练样本的真实值，a_j⁽ⁱ⁾为第i层的第j个单元的激励值。这里对上式进行向量化表示为ξ⁽ⁱ⁾=a⁽ⁱ⁾-y⁽ⁱ⁾，ξ、a、y都是尺寸为(K * 1)的向量。既然叫做反向传播，显然就是先求最后一层也就是output layer的每个输出单元对应的误差，然后求倒数第二层ξ^(L-1)，倒数第三层ξ^(L-2)，一直求到第二层ξ⁽²⁾。第一层ξ⁽¹⁾是没有的，因为第一层是input layer，不存在误差。计算公式如下

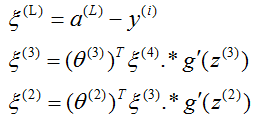这里的 .* 代表向量间对应元素的乘积。式中的g'(z⁽³⁾) = g(z⁽³⁾) * (1-g(z⁽³⁾))，这个证明只要对g(z)=1/(1+e^(-z))求导就可以看出来。

求出了各单元的误差之后，再计算

上面的这些计算都需要遍历整个数据集，也就是放在一个for循环中，在遍历了所有数据集之后跳出for循环，执行

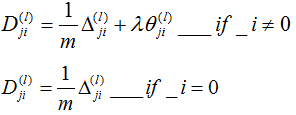可以证明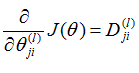，求出了代价函数的偏导数之后我们就可以应用梯度下降法或者其他高级算法了

　　3、梯度检验

　　当我们对神经网络应用梯度下降法时，可能会存在一些不易察觉的错误，虽然代价函数可能确实在减小，为了避免这种情况，我们采用的方法叫梯度检验。对某一点梯度的估计可以采用与其较近的两点的梯度的平均，即我们要估计θ这点的梯度，就选取一个很小的常数ε，利用θ+ε和θ-ε这两点的梯度的平均代替θ的梯度。当ε趋于0时，也就是θ点的真实梯度了。

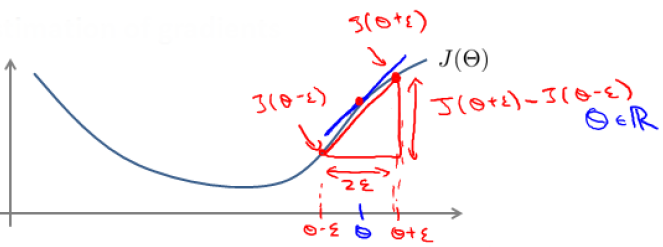
所以这里的梯度我们表示为。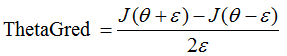

当θ不再是一个数而是一个向量时，上式变为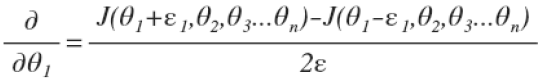，对每个θ_i都进行同样的操作即可。

　　我们用梯度检验算法得到ThetaGred后，与反向传播法计算出来的偏导数进行比较，两者最多差几个小数位，这是就可以认为我们的反向传播法是正确且有效的。在进行完比较之后，我们需要关闭梯度检测法的程序，因为这种方法求偏导数的效率很低，如果不关闭的话程序就会运行很长时间。

　　4、参数随机初始化

　　我们之前的方法都是对参数初始化赋0值，这样对逻辑回归是可以的，但是对神经网络来说就会出现问题。当我们对神经网络input layer的参数初始化赋0时，我们得到的第二层的激励都会是一个相同的值，不光是初始化为0，初始化为其他任意的一个常数都会有同样的结果。所以这里我们需要对参数进行随机初始化，通常我们会选择在-ε~+ε之间的随机值。θ=random(j,i) * 2ε-ε，θ是一个j * i的矩阵。

　　5、总结

　　总结一下神经网络的步骤：

　　(1)确定网络结构

　　　　input layer的单元数即我们训练集的特征数量

　　　　output layer的单元数是我们训练结果的类的数量

　　　　hidden layer一般就选一层，单元数稍大于input layer单元数即可。如果hidden layer大于一层，我们应该确保所有的隐藏层的单元数都相同。

　　(2)训练神经网络

　　　　参数的随机初始化

　　　　利用正向传播法计算所有的a_j⁽ⁱ⁾即h_θ(x)

　　　　编写计算代价函数J的代码

　　　　利用反向传播法计算所有偏导数

　　　　利用数值梯度检验算法检验偏导数

　　　　使用优化算法来最小化代价函数J