相关与卷积（数字信号处理）的数学原理及 Python 实现

数学原理

　　在数字信号处理中，相关(correlation)可以分为互相关(cross correlation)和自相关(auto-correlation). 互相关是两个数字序列之间的运算；自相关是单个数字序列本身的运算，可以看成是两个相同数字序列的互相关运算．互相关用来度量一个数字序列移位后，与另一个数字序列的相似程度．其数学公式如下：

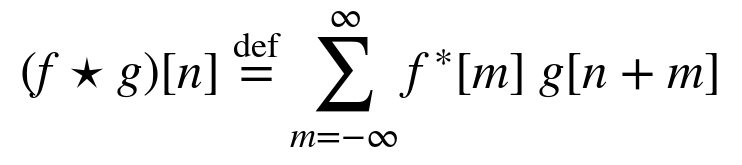
　　其中，f 和 g 为数字序列，n 为移位的位数，f^* 表示 f 序列值的复数共轭，即复数的实部不变，虚部取反．

　　而卷积（convolution）与互相关运算相似，定义为将其中一个序列反转并移位后，两个序列的乘积的积分（求和），其数学公式如下：

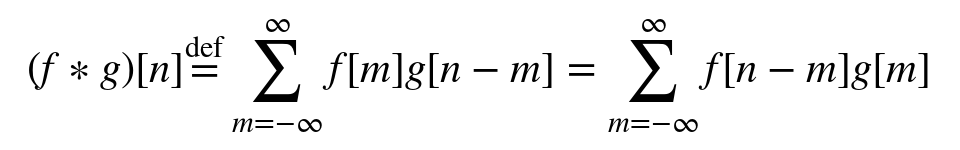
　　其中，f 和 g 为数字序列，n 为移位的位数.

　　在实数范围内，f 的复数共轭 f^* = f ．此时，通过比较上面两式可知：序列 f 与将序列 g 反转后的序列的卷积为序列 f 与序列 g 的互相关

 

Python 实现

采用两种方式实现：自定义互相关函数和直接调用 numpy.correlate 或 numpy.convolve．

　　在 numpy 中, numpy.correlate 函数实现两个一维数组的互相关操作；numpy.convolve 实现了两个一维数组的卷积操作．其中定义了三种模式（'valid', 'same','full'）.

　　设两个序列长度分别为 M 和 N，则

• 'valid' 模式：输出长度为 max(M,N)-min(M,N)+1．只返回两个序列完全重合部分的点的卷积或相关运算；
• 'same' 模式：输出长度为两个序列中的较长者，即 max(M,N)；
• 'full' 模式：输出长度为 M+N-1, 返回所有包含重叠部分的点.

　　互相关或卷积，实际上，就是计算两个序列（一维数组）在不同移位情况下，两个序列逐位相乘之后，求和的结果．不同模式只是返回互相关或卷积结果的不同部分．
　　注：如果在超出数组的索引范围，用 0 填充．

下面代码，采用自定义函数 correlate_func (只适用于实数值) 实现 numpy.correlate 和 numpy.convolve 的三种模式，并进行测试．

#!//usr/bin/env python
# -*- coding: utf8 -*-
"""
# Author: klchang
# Description: correlation or convolution of  one-dimensional array with real numbers.
# Date: 2018.11
"""
from __future__ import print_function
import numpy as np


def correlate_func(a, b, mode='valid', conv=True):
    '''correlation or convolution in 1-d array with real numbers'''
    if a is None or b is None:
        return None
    if len(a) > len(b):# Ensure the length of a is no longer than that of b.
        return correlate_func(b, a, mode)

    # Convert to np.array type
    a, b = list(map(np.array, [a, b]))
    if conv: a = a[::-1]  # if convolution is true, reverse the shorter 
    res = []
    min_len, max_len = len(a), len(b)
    if mode == 'valid':
        output_length = max_len - min_len + 1
        tmp = b
    elif mode == 'same':
        output_length = max_len
        tmp = np.hstack((np.zeros(min_len-1), b))
    elif mode == 'full':
        output_length = max_len + min_len - 1
        tmp = np.hstack((np.zeros(min_len-1), b, np.zeros(min_len-1)))
    else:
        raise Exception("No such mode {}!".format(mode))

    # For each point, get the total sum of element-wise multiplication
    for i in range(output_length):
        val = np.sum(a * tmp[i:min_len+i])
        res.append(val)
    return np.array(res, dtype=a.dtype)


def test():
    a = [1, 2, 3]
    b = [1, 2]
    names = ['numpy.correlate', 'correlate_func', 'numpy.convolve', 'correlate_func(convolution)']
    funcs = [np.correlate, correlate_func, np.convolve, lambda *args: correlate_func(*args, conv=True)]
    for i, (name, func) in enumerate(zip(names, funcs)[:4]):
        print ('-----' * 30 if i & 0x01 == 0 else '')
        print ("{} output result: ".format(name))
        print ('    valid mode: ', func(a, b, 'valid'))
        print ('    same mode: ', func(a, b, 'same'))
        print ('    full mode: ', func(a, b, 'full'))

if __name__ == '__main__':
    test()

除此之外，在 matplotlib.pyplot 模块中，实现了用于可视化的自相关函数 matplotlib.pyplot.acorr 和互相关函数 matplotlib.pyplot.xcorr, 官方网址提供的一个示例代码如下:

import matplotlib.pyplot as plt
import numpy as np


np.random.seed(0)

x, y = np.random.randn(2, 100)
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.xcorr(x, y, usevlines=True, maxlags=50, normed=True, lw=2)
ax1.grid(True)
ax1.axhline(0, color='black', lw=2)

ax2 = fig.add_subplot(212, sharex=ax1)
ax2.acorr(x, usevlines=True, normed=True, maxlags=50, lw=2)
ax2.grid(True)
ax2.axhline(0, color='black', lw=2)

plt.show()

参考资料

[1] Cross-correlation - Wikipedia. https://en.wikipedia.org/wiki/Cross-correlation

[2] Convolution - Wikipedia. https://en.wikipedia.org/wiki/Convolution

[3] Python: Interpretation on XCORR. https://stackoverflow.com/questions/24396589/python-interpretation-on-xcorr

[4] numpy.correlate - Numpy Reference. https://docs.scipy.org/doc/numpy/reference/generated/numpy.correlate.html

[5] numpy.convolve - Numpy Reference. https://docs.scipy.org/doc/numpy/reference/generated/numpy.convolve.html#numpy.convolve