算法导论之摊还分析学习笔记

基本原理

在摊还分析(amortized analysis)中, 通过求数据结构的一个操作序列中的所有操作的平均执行时间, 来评价操作的代价. 摊还分析不同于平均情况分析, 它并不涉及概率, 可以保证最坏情形下每个操作的平均性能.
常用的三种技术: 聚合分析(aggregate analysis), 记账法(accounting method)和势能法(potential method).
聚合分析用来确定一个序列(内有 n 个操作)的总代价的上界 T(n). 因而每个操作的平均代价为 T(n)/n. 聚合分析方法将平均代价作为每个操作的摊还代价, 即所有操作(可能包含多个类型的操作)具有相同的摊还代价.
记账法和势能法都可用来分析每个操作的摊还代价. 当存在不止一种类型的操作时, 其摊还代价可能不同.

记账法将序列中某些较早的操作的余额(overcharge)作为预付信用(prepaid credit)储存起来, 与数据结构中的特定对象相关联, 在操作序列中的随后部分, 储存的信用即可用来为那些缴费少于实际代价的操作支付差额. 赋予一个操作的费用称为这个操作的摊还代价. 用记账法(accounting method)进行摊还分析时, 不同的操作可能有不同的摊还代价, 某些操作的摊还代价可能多于或少于其实际代价. 当一个操作的摊还代价超过其实际代价时, 将其差额存入数据结构中的特定对象, 存入的差额称为信用(credit).

势能法也是通过较早操作的余额来补偿稍后操作的差额. 与记账法不同, 势能法将余额作为一个整体(即数据结构的势能)存储, 而不是将信用与数据结构中单个对象关联并分开存储. 势函数将每个数据结构映射到一个实数, 此值即为关联到该数据结构的势. 注意, 势是非负的, 但第 i 个操作的势差可能是负的, 从而导致摊还代价为负.

示例: 动态表(Dynamic Tables)

应用摊还分析方法分析动态扩张和收缩表(动态表, dynamic table)的问题.

学习目标
证明, 虽然动态表的插入(TABLE-INSERT)和删除(TABLE-DELETE)操作可能引起表的扩张或收缩, 有较高的实际代价,但它们的摊还代价都是O(1);
而且, 如何保证动态表中的空闲空间相对于总空间的比例永不超过某个常数分数.

槽(slot)定义为保存一个数据项的空间;
非空表 T (non-empty table)的的装载因子 α(T) 定义为表中存储的数据项的数量除以表的规模(槽的数量); 对于空表(没有数据项), 其规模为 0, 将其装载因子(load factor)设定为 1．

TABLE-INSERT 操作将一个数据项插入表中, 占用一个槽; TABLE-DELETE 操作从表中删除一个数据项;
表扩张(table expansion)是由于对于某些应用程序, 无法预知会有多少个对象存储在表中. 我们会先分配一定的内存空间, 当发现不够用时, 必须为其重新分配更大的空间, 并将所有对象从原表复制到新的空间. 释放原有的空间; 简单说, 扩张表(expand table)通过分配一个包含更多槽的新表来实现.
表收缩(table contraction)是从表中删除了很多对象后, 为提高内存空间的利用率, 值得为其重新分配更少的空间. 具体来说, 当表中的数据项下降得太少时, 首先分配一个新的更少的表空间, 然后将数据项从旧表复制到新表中, 之后释放旧表占用的内存空间, 将其归还内存管理系统.
理想情况下, 希望保持两个性质:

• 动态表的装载因子有一个正的常数的下界;
• 一个表操作的摊还代价有一个常数下界. 

当对满表(full table)进行插入数据项操作时, 需要将表的规模(table size)加倍, 以存放新的数据项, 同时又避免了频繁重新分配内存.
常用的启发式策略(heuristic)是: 为新表分配两倍于旧表的槽(内存空间). 如果只允许插入操作, 那么装载因子总会保持在1/2以上, 因此, 浪费的空间永远不会超过总空间的一半.

TABLE-INSERT 操作的伪代码, 如下:

其中, T 是一个对象, 对应表. 属性 T.table 保存指向表的存储空间的指针; T.num 保存表中的数据项数量; T.size 保存表的规模(槽数, the total number of slots in a table). 初始时, 令表为空: T.num = T.size = 0.

只有表扩张(TABLE-INSERTION)这一种操作时, 在执行 n 个 TABLE-INSERTION 操作的过程中, 仅当 i-1 恰为 2 的幂时, 第 i 个操作才会引起1次表扩张, 下面使用上述的3种方法来分析:
采用聚合分析法, 第 i 个操作的代价为

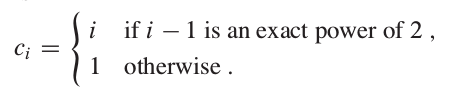
所以, n 个 TABLE-INSERTION 操作的总代价为

采用记账法分析, 一次 TABLE-INSERTION 操作的摊还代价为 3. 直观上, 可以理解为处理每个数据项需付出3次基本插入操作的代价: 将当前数据项插入到当前表中; 表扩张时, 移动本数据项的代价; 表扩张时, 移动另一个已经移动过的数据项的代价.

采用势能法分析 n 个TABLE-INSERTION 操作序列. 定义势函数Φ,在表扩张后,其值为0; 表满时, 其值为表的规模, 以用来支付下次扩张表的代价. 势函数可以定义为

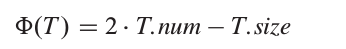
其中, T 是一个对应表的对象; T.num 为表中数据项数量; T.size 为表的规模(槽数). 当进行一次表扩张后, 有 T.num = T.size/2, 此时有 Φ(T) = 0; 而在表扩张之前, 有 T.num = T.size, 此时 Φ(T) = T.num. 势函数初值为0(T.num = T.size = 0), 且表都是至少是半满的, 即 T.num >= T.size/2, 于是 Φ(T) 总是非负的. 因此 n 个TABLE-INSERTION 操作的摊还代价之和给出实际代价之和的上界, 即

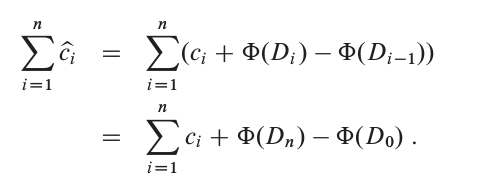
其中, D₀为初始数据结构; c_i为每个操作的实际代价; 为每个操作的摊还代价

每个操作的摊还代价等于其实际代价与此操作引起的势能变化之和.

分析第 i 个 TABLE-INSERT 操作的摊还代价. 令 num_i 表示第 i 个操作后表中数据项的数量, size_i 表示第i个操作后,表的总规模, Φ_i 表示第 i 个操作后的势.
初始时, num₀ = size₀ = Φ₀ = 0,然后分两种情况进行讨论:
1) 第 i 个TABLE-INSERT操作没有触发表扩张. 此时有 size_i = size_i-1 及 num_i-1 = num_i - 1 < size_i-1. 第 i 个操作的摊还代价为

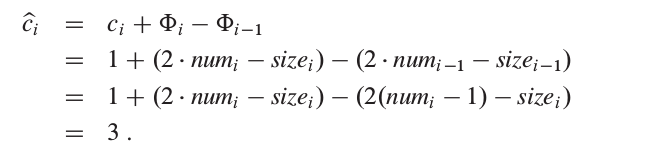
2) 第 i 个TABLE-INSERT操作触发表扩张. 此时有 size_i = 2 * size_i-1 及 size_i-1 = num_i-1 = num_i - 1. 第 i 个操作的摊还代价为

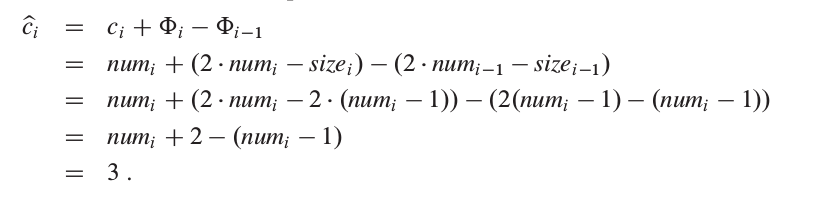
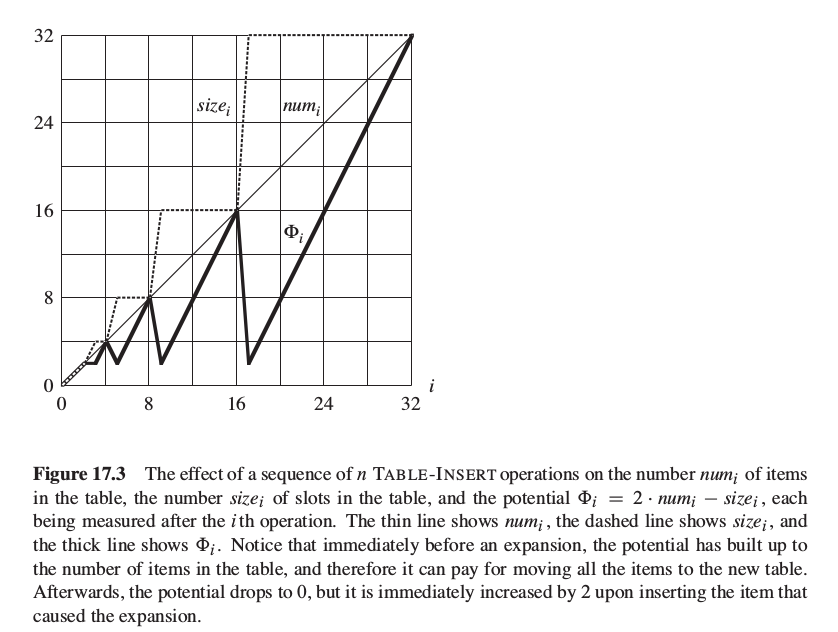
下图中, 绘制出了 num_i, size_i 和 Φ_i 随 i 变化的情况. 注意, 势(potential)是如何累积来支付表扩张的代价的. 每次插入数据项(摊还代价为3), 去掉插入本数据项所需的代价(实际代价为1), 将未消耗的代价(即 2)存入势(potential)中, 进行累积. 

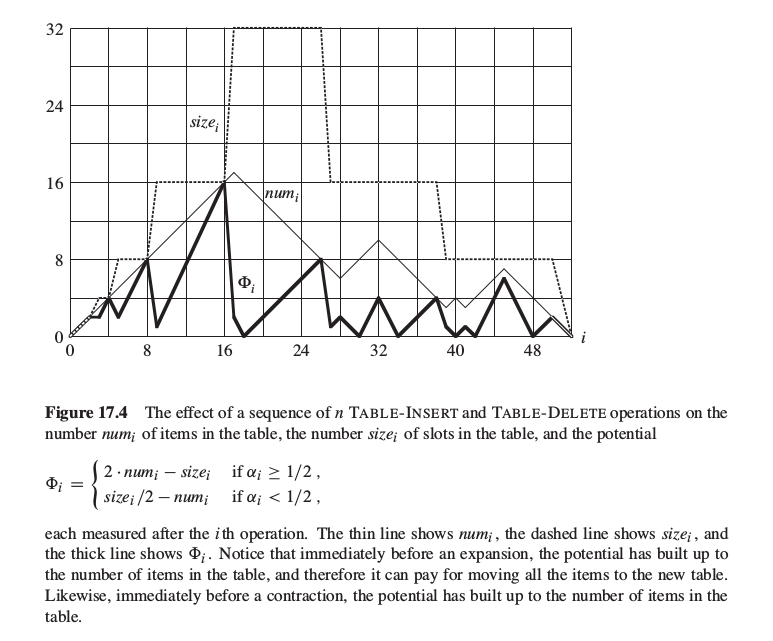
表扩张和收缩采用的常用策略是允许表的装载因子低于1/2. 具体地, 当向一个满表, 插入一个新数据项时, 将表规模加倍; 但只有当装载因子小于1/4而不是1/2时, 将表的规模减半.

下面采用势能法分析n个TABLE-INSERT和TABLE-DELETE操作组成的序列的代价.

首先定义一个势函数Φ, 满足在表扩张或表收缩之后, 其值为 0, 而当装载因子增长为 1 或下降为 1/4 时, 势函数值累积到足够支付表扩张或表收缩操作的代价值. 势函数的具体定义如下:

可以在下图中观察到势函数的这些特性.

令 c_i 表示第 i 个操作的实际代价,  ^c_i 表示用势函数 Φ 定义的摊还代价, num_i 表示表中第 i 个操作存储的数据项的数量, size_i 表示第 i 个操作后,表的规模, α_i 表示第 i 个操作后的装载因子, Φ_i 表示第i个操作后的势. 初始时, num₀ = size₀ = 0, α₀=1, Φ₀ = 0.

下面分别分析第 i 个操作是 TABLE-INSERT或TABLE-DELETE的情况:
a) 当第 i 个操作为TABLE-INSERT时，总有 num_i = num_i-1 + 1
1) 若 α_i-1 >= 1/2, 则与上面"采用势能法分析 n 个TABLE-INSERTION 操作序列"的情况相同. 无论表是否扩张, 操作的摊还代价至多都是 3;
2) 若 α_i-1 < 1/2, 则第 i 个操作不能令表扩张, 即表规模不变( size_i = size_i-1), 因为只有当 α_i-1 = 1时, 第i个TABLE-INSERT操作才会引起表扩张.
2.1) 若 α_i < 1/2, 则第 i 个操作的摊还代价为

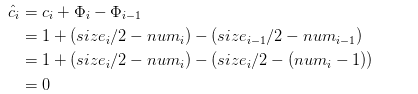
2.2) 若 α_i >= 1/2, 则第 i 个操作的摊还代价为

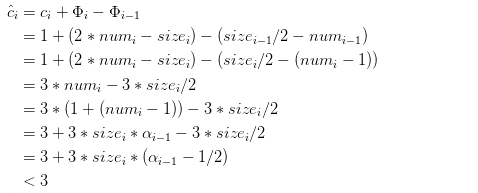
注: num_i-1 = num_i - 1 = size_i * α_i-1 < size_i/2 <= size_i * α_i

b) 当第ｉ个操作为TABLE-DELETE时，总有 num_i = num_i-1 - 1
1) 若 α_i-1 < 1/2, 则必须考虑删除操作是否引起表收缩．
1.1) 若第ｉ个操作未引起表收缩，此时α_i >= 1/4 ，则 size_i = size_i-1, 此时TABLE-DELETE操作的摊还代价为

1.2) 若第ｉ个操作触发了表收缩(装载因子α_i-1 = num_i-1/size_i-1 = 1/4)，则有 size_i = size_i-1/2 = 2*num_i-1= 2*(num_i+1)，且操作的实际代价为 c_i = num_i+1，因为删除1个数据项，之后又移动了 num_i 个数据项, 此时 TABLE-DELETE 操作的摊还代价为

2) 若α_i-1 >= 1/2, 则第ｉ个操作不能引起表收缩, 即表规模不变(size_i = size_i-1)
2.1) 若 α_i >= 1/2，则第ｉ个操作的摊还代价为

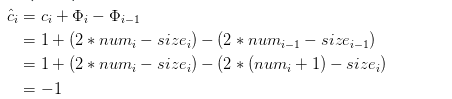
2.2) 若 α_i < 1/2，此时装载因子α_i-1 = num_i-1/size_i-1 = (num_i+1)/size_i= 1/2, 则第 i 个操作的摊还代价为

综上可知，每个操作的摊还代价的上界是一个常数，所以在一个动态表上执行任意 n 个操作的运行时间是 O(n).

练习及解答

17.4-3 假定我们改变表收缩的方式, 不是当装载因子小于1/4时将表规模减半, 而是当装载因子小于1/3时将表规模变为原来的2/3. 使用势函数
Φ(T) =| 2 * T.num - T.size |
证明使用此策略, TABLE-DELETE 操作的摊还代价的上界是一个常数.

解答

分析第 i 个 TABLE-DELETE 操作, 此时有 num_i = num_i-1-1.
若 α_i-1 < 1/2, 则必须考虑删除操作是否引起表收缩. 如果没有引起收缩 , 则 size_i = size_i-1, 且操作的摊还代价为

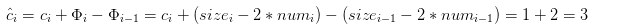
若 α_i-1 < 1/2 且 第 i 个操作触发了收缩操作, 即装载因子小于1/3(num_i/size_i < 1/3), 则 size_i = 2 * size_i-1/3, 此时操作的实际代价为 c_i = num_i+1, 因为我们删除了 1 个数据项, 又移动了 num_i 个数据项. 因此操作的摊还代价为

若 α_i-1 >= 1/2 则操作的摊还代价为

所以, 每个TABLE-DELETE操作的摊还代价的上界是一个常数. 

参考资料

[1] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms (3. ed.). MIT Press, 2009.
[2] (美)科尔曼(Cormen, T.H.)等著，殷建平等译. 算法导论(原书第3版). 北京: 机械工业出版社, 2013.1
[3] 算法导论习题解答 17-4-3. https://blog.csdn.net/weixin_42369181/article/details/105469860