(说明:本博客中的题目、题目详细说明及参考代码均摘自 “何海涛《剑指Offer:名企面试官精讲典型编程题》2012年”)
题目
1. 写一个函数,输入 n, 求斐波那契(Fibonacci)数列的第 n 项。斐波那契数列的定义如下:

2. 一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级。求该青蛙跳上一个n级的台阶总共有多少种跳法?
3. 一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级,...... ,也可以跳上n级,此时该青蛙跳上一个 n 级的台阶共有多少种跳法?
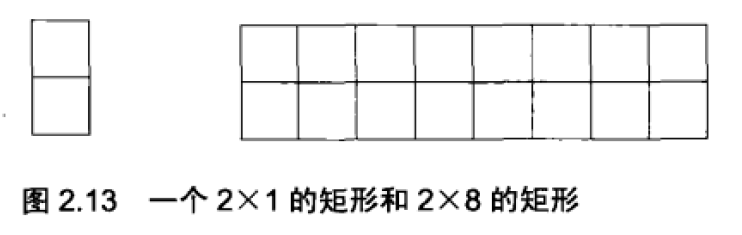
4. 用 2x1 (图 2.13 的左边)的小矩形横着或者竖着去覆盖更大的矩形。请问用 8 个 2x1 小矩形无重叠地覆盖一个 2x8 的大矩形(图 2.13 的右边),总共有多少种方法?
题目解析
本博客提及到 4 个题目:题目 1 直接给出斐波那契数列的定义,可采用多种算法实现,这些算法思想将在 “算法设计思想“ 部分介绍;题目 2 和题目 4 的本质上解决的还是斐波那契数列第 n 项的计算问题,即题目 1;题目 3 可以说是数学问题,只要意识到其计算的实质上是 2 的 n 次幂即可,剩下的工作采用程序就很容易实现了。
下面具体说如何理解题目 2、题目 3 和 题目4:
- 对于题目 2,青蛙每次只能跳上 1 级或 2 级台阶。假定青蛙需要跳上 n 级台阶,其可能的组合数为 g(n) 。青蛙第 1 次跳台阶有 2 种可能:跳上 1 级台阶,剩余 n-1 级台阶;跳上 2 级台阶,剩余 n-2 级台阶。所以 g(n) = g(n-1) + g(n-2),即青蛙跳上 n 级台阶的可能的组合数等于第 1 次跳上 1 级台阶的可能组合数加上第 1 次跳上 2 级台阶的可能组合数。也可理解为以何种方式跳上第 n 级台阶(跳上 1 级台阶,还是跳上 2 级台阶)。至此,就转化为求解斐波那契数列的第 n 项问题。
- 对于题目 3,与题目 2 相比,区别在于青蛙每次可以跳上任意级台阶,不仅仅是 1 级或 2 级台阶。如果此时青蛙需要跳上 n 级台阶,可采取的跳法有 f(n) = 2n-1 种。可以采用数学归纳法证明,具体证明思路如下:
当 n = 1或 n = 2 时, 显然成立;
令 n = k 时, f(k) = 2k-1 成立,当 n = k+1 时,f(k+1) = f(k) + f(k-1) + f(k-2) + ... + f(1) + 1. 在增加 1 级台阶后,可以理解为,设青蛙在跳上最后一级台阶(新增加的台阶)时,所跳上的台阶数为 x,若 x = 1,则此时可采跳法是 f(k) 种跳法;若 x = 2,则此时可采取的跳法为 f(k-1); 如此下去,一直到 x = k-1 时,则此时可采取的跳法为 f(1);除此之外,还需要加上一种 x = k+1 可能,即只需一次直接跳上 k+1 级台阶。又因为

- 对于题目 4,使用图 2.13 左图 (2x1的矩形,也可变换为1x2矩形,设为形状A) 填充图 2.13 的右图 (2x8的矩形,设为形状B(8),其中8为列数) 时,如果先放置一块,有两种放法,一种横着放,一种是竖着放。如果第一次横着放,则下一个也必须是横着放,此时问题变为使用形状 A 填充形状 B(6);如果第一次是竖着放,则问题变为使用形状 A 填充形状 B(7)。为了表示方便,则依旧用相同的符号 B 表示为用 A 填充 B 的方法数,则有 B(8) = B(6) + B(7),从递推公式可以看出,这是一个斐波那契数列的问题。
算法设计思想
1. 递归方法(Recursive Method)。循环调用自身。缺点:有大量的重复计算,不实用。优点:实现非常简单,代码短小。对于斐波那契数列的实现,其时间复杂度为 O(2n)。
2. 迭代方法 (Iterative Method)。通过循环,替代递归方法,从理论上说,任何递归算法都可用迭代算法实现。优点:节省栈空间,有可能降低时间复杂度。缺点是相对于递归方法,实现较难,代码往往会复杂一些。对斐波那契数列,其时间复杂度为 O(n),是比较实用的算法。
3. 公式法。通过不常用的计算斐波那契数列的第 n 项的数学公式,如果采用合适的实现方式,可将时间复杂度降为 O(logn),具体数学公式和相关说明如下(摘自参考资料):

C++ 实现
#include <iostream>
// Method 1: recursive method and its time complexity is O(2^n).
int fibonacciRecursively(int n)
{
int result;
if (n <= 0)
result = 0;
else if (1 == n)
result = 1;
else
result = fibonacciRecursively(n-1) + fibonacciRecursively(n-2);
return result;
}
// Method 2: iterative method and its time complexity is O(n).
int fibonacciIteratively(int n)
{
int result = 0;
int nextItem = 1;
for (int i = 1; i <= n; ++i)
{
int tmp = nextItem;
nextItem += result;
result = tmp;
}
return result;
}
// Method 3: by means of the specified matrix power
long int* matrixPower(long int *mat, int n); // compute the power of the matrix
int fibonacciMatrixPower(int n)
{
long int matrix[] = {1, 1, 1, 0};
int result = 0;
if (n <= 0)
result = 0;
else
{
matrixPower(matrix, n-1);
result = matrix[0];
}
return result;
}
// 2 x 2 matrix power, n >= 0
long int* matrixPower(long int *mat, int n)
{
const int rows = 2;
const int cols = 2;
if (n <= 0)
return NULL;
else if (0 == n)
{
// identity matrix when the power of a matrix is 0.
for (int i = 0; i < rows; ++i)
for (int j = 0; i < cols; ++j)
{
if (i == j)
*(mat + i * cols + j) = 1;
else
*(mat + i * cols + j) = 0;
}
}
else if (1 == n)
{
}
else if (2 == n)
{
// Create two temporary arrays for matrix multiplication
long int tmpMat1[4], tmpMat2[4];
for (int i = 0; i < rows; ++i)
for (int j = 0; j < cols; ++j)
{
tmpMat1[i*cols+j] = *(mat + i * cols + j);
tmpMat2[i*cols+j] = *(mat + i * cols + j);
}
// matrix multiplication
*(mat + 0 * cols + 0) = tmpMat1[0*cols+0] * tmpMat2[0*cols+0] + tmpMat1[0*cols+1] * tmpMat2[1*cols+0]; // matrix{0,0}
*(mat + 0 * cols + 1) = tmpMat1[0*cols+0] * tmpMat2[0*cols+1] + tmpMat1[0*cols+1] * tmpMat2[1*cols+1]; // matrix{0,1}
*(mat + 1 * cols + 0) = tmpMat1[1*cols+0] * tmpMat2[0*cols+0] + tmpMat1[1*cols+1] * tmpMat2[1*cols+0]; // matrix{1,0}
*(mat + 1 * cols + 1) = tmpMat1[1*cols+0] * tmpMat2[0*cols+1] + tmpMat1[1*cols+1] * tmpMat2[1*cols+1]; // matrix{1,1}
}
else if (n % 2 == 0) // when n is even and n is greater than 2
{
matrixPower(mat, n/2);
matrixPower(mat, 2);
}
else // n is odd and n is greater than 2
{
long int tmpMat1[4];
for (int k = 0; k < 4; ++k)
tmpMat1[k] = *(mat + k);
// Compute matrix power in even case
matrixPower(mat, n-1);
// Temporarily save the matrix
long int tmpMat2[4];
for (int k = 0; k < 4; ++k)
tmpMat2[k] = *(mat + k);
// matrix multiplication with additional element.
*(mat + 0 * cols + 0) = tmpMat1[0*cols+0] * tmpMat2[0*cols+0] + tmpMat1[0*cols+1] * tmpMat2[1*cols+0];
*(mat + 0 * cols + 1) = tmpMat1[0*cols+0] * tmpMat2[0*cols+1] + tmpMat1[0*cols+1] * tmpMat2[1*cols+1];
*(mat + 1 * cols + 0) = tmpMat1[1*cols+0] * tmpMat2[0*cols+0] + tmpMat1[1*cols+1] * tmpMat2[1*cols+0];
*(mat + 1 * cols + 1) = tmpMat1[1*cols+0] * tmpMat2[0*cols+1] + tmpMat1[1*cols+1] * tmpMat2[1*cols+1];
}
return mat;
}
void unitest()
{
int n = 5;
std::cout << "The " << n << "-th item in the fibonacci sequence:
"
<< " Recursive method result: " << fibonacciRecursively(n) << std::endl
<< " Iterative method result: " << fibonacciIteratively(n) << std::endl
<< " Matrix power method result: " << fibonacciMatrixPower(n) << std::endl
;
}
int main()
{
unitest();
return 0;
}
Python 实现
#!/usr/bin/python
# -*- coding: utf8 -*-
# Method 1: recursive method
def fib_recursively(n):
result = 0
if n >= 1:
if 1 == n:
result = 1
else:
result = fib_recursively(n-1) + fib_recursively(n-2)
return result
# Method 2: iterative method
def fib_iteratively(n):
result, next_item = 0, 1
i = 1
while i <= n:
result, next_item = next_item, result + next_item
i += 1
return result
# Method 3: matrix power
def fib_matrix_power(n):
matrix = [1, 1, 1, 0]
result = 0
if n > 0:
matrix_power(matrix, n-1)
result = matrix[0]
return result
# 2 x 2 matrix power
def matrix_power(mat, n):
rows, cols = 2, 2 # 2 x 2 matrix
if n <= 0:
return None
elif 0 == n:
mat[:] = [1, 0, 0, 1] # identity matrix
elif 1 == n:
pass
elif 2 == n:
tmp_mat1, tmp_mat2 = [], []
tmp_mat1.extend(mat)
tmp_mat2.extend(mat)
# matrix multiplication
for i in range(rows):
for j in range(cols):
mat[i*cols+j] = inner_product(tmp_mat1[i::cols], tmp_mat2[j::cols])
elif n % 2 == 0: # even case
matrix_power(mat, n/2)
matrix_power(mat, 2)
else:
# temporarily save mat
tmp_mat1 = []
tmp_mat1.extend(mat)
# recursive call
matrix_power(mat, n-1)
# multiply with former temporary value
tmp_mat2 = []
tmp_mat2.extend(mat)
for i in range(rows):
for j in range(cols):
mat[i*cols+j] = inner_product(tmp_mat1[i::cols], tmp_mat2[j::cols])
return mat
def inner_product(vec1, vec2):
product = 0
if (vec1 and vec2 and len(vec1) == len(vec2)):
for i in range(len(vec1)):
product += vec1[i] * vec2[i]
return product
if __name__ == '__main__':
n = 5
print("The %d-th item in the fibonacci sequence:" % n)
print(" Recursive method result: %d" % fib_recursively(n))
print(" Iterative method result: %d" % fib_iteratively(n))
print(" Matrix power method result: %d" % fib_matrix_power(n))
参考代码
1. targetver.h
#pragma once
// The following macros define the minimum required platform. The minimum required platform
// is the earliest version of Windows, Internet Explorer etc. that has the necessary features to run
// your application. The macros work by enabling all features available on platform versions up to and
// including the version specified.
// Modify the following defines if you have to target a platform prior to the ones specified below.
// Refer to MSDN for the latest info on corresponding values for different platforms.
#ifndef _WIN32_WINNT // Specifies that the minimum required platform is Windows Vista.
#define _WIN32_WINNT 0x0600 // Change this to the appropriate value to target other versions of Windows.
#endif
2. stdafx.h
// stdafx.h : include file for standard system include files,
// or project specific include files that are used frequently, but
// are changed infrequently
//
#pragma once
#include "targetver.h"
#include <stdio.h>
#include <tchar.h>
// TODO: reference additional headers your program requires here
3. stdafx.cpp
// stdafx.cpp : source file that includes just the standard includes
// Fibonacci.pch will be the pre-compiled header
// stdafx.obj will contain the pre-compiled type information
#include "stdafx.h"
// TODO: reference any additional headers you need in STDAFX.H
// and not in this file
4. Fibonacci.cpp
// Fibonacci.cpp : Defines the entry point for the console application.
//
// 《剑指Offer——名企面试官精讲典型编程题》代码
// 著作权所有者:何海涛
#include "stdafx.h"
// ====================方法1:递归====================
long long Fibonacci_Solution1(unsigned int n)
{
if(n <= 0)
return 0;
if(n == 1)
return 1;
return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);
}
// ====================方法2:循环====================
long long Fibonacci_Solution2(unsigned n)
{
int result[2] = {0, 1};
if(n < 2)
return result[n];
long long fibNMinusOne = 1;
long long fibNMinusTwo = 0;
long long fibN = 0;
for(unsigned int i = 2; i <= n; ++ i)
{
fibN = fibNMinusOne + fibNMinusTwo;
fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
}
return fibN;
}
// ====================方法3:基于矩阵乘法====================
#include <cassert>
struct Matrix2By2
{
Matrix2By2
(
long long m00 = 0,
long long m01 = 0,
long long m10 = 0,
long long m11 = 0
)
:m_00(m00), m_01(m01), m_10(m10), m_11(m11)
{
}
long long m_00;
long long m_01;
long long m_10;
long long m_11;
};
Matrix2By2 MatrixMultiply
(
const Matrix2By2& matrix1,
const Matrix2By2& matrix2
)
{
return Matrix2By2(
matrix1.m_00 * matrix2.m_00 + matrix1.m_01 * matrix2.m_10,
matrix1.m_00 * matrix2.m_01 + matrix1.m_01 * matrix2.m_11,
matrix1.m_10 * matrix2.m_00 + matrix1.m_11 * matrix2.m_10,
matrix1.m_10 * matrix2.m_01 + matrix1.m_11 * matrix2.m_11);
}
Matrix2By2 MatrixPower(unsigned int n)
{
assert(n > 0);
Matrix2By2 matrix;
if(n == 1)
{
matrix = Matrix2By2(1, 1, 1, 0);
}
else if(n % 2 == 0)
{
matrix = MatrixPower(n / 2);
matrix = MatrixMultiply(matrix, matrix);
}
else if(n % 2 == 1)
{
matrix = MatrixPower((n - 1) / 2);
matrix = MatrixMultiply(matrix, matrix);
matrix = MatrixMultiply(matrix, Matrix2By2(1, 1, 1, 0));
}
return matrix;
}
long long Fibonacci_Solution3(unsigned int n)
{
int result[2] = {0, 1};
if(n < 2)
return result[n];
Matrix2By2 PowerNMinus2 = MatrixPower(n - 1);
return PowerNMinus2.m_00;
}
// ====================测试代码====================
void Test(int n, int expected)
{
if(Fibonacci_Solution1(n) == expected)
printf("Test for %d in solution1 passed.
", n);
else
printf("Test for %d in solution1 failed.
", n);
if(Fibonacci_Solution2(n) == expected)
printf("Test for %d in solution2 passed.
", n);
else
printf("Test for %d in solution2 failed.
", n);
if(Fibonacci_Solution3(n) == expected)
printf("Test for %d in solution3 passed.
", n);
else
printf("Test for %d in solution3 failed.
", n);
}
int _tmain(int argc, _TCHAR* argv[])
{
Test(0, 0);
Test(1, 1);
Test(2, 1);
Test(3, 2);
Test(4, 3);
Test(5, 5);
Test(6, 8);
Test(7, 13);
Test(8, 21);
Test(9, 34);
Test(10, 55);
Test(40, 102334155);
return 0;
}
5. 参考代码下载
项目 09_Fibonacci 下载: 百度网盘
何海涛《剑指Offer:名企面试官精讲典型编程题》 所有参考代码下载:百度网盘
参考资料
[1] 何海涛. 剑指 Offer:名企面试官精讲典型编程题 [M]. 北京:电子工业出版社,2012. 71-77.