二维凸包算法学习笔记

开始补一些算几的东西。

定义引入

凸包到底是个什么东西呢？

在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1，...Xn)的凸组合来构造.

——摘自百度百科

有没有整个人都mengbi了

对于二维凸包，有一个很形象的描述：

平面上有若干颗钉子，现在绷一圈橡皮筋把所有的钉子都围住，松手之后橡皮筋的形状就是凸包。

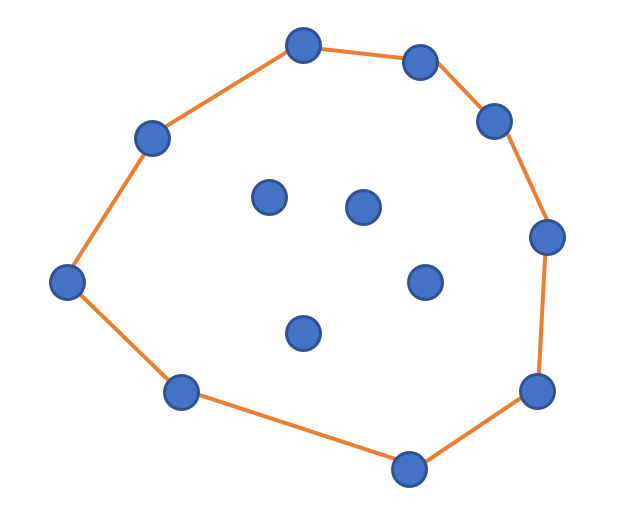
如图的橙色线段是这个点集的凸包。

---

先来看一道例题：

圈奶牛

题意是要求凸包的长度。先把点用结构体存一下，注意读入的时候不要用读优！不要用读优！不要用读优！

重要的事情说三遍都不够。调了一个小时的血泪史

当然如果你写了小数读优当我没说

我们的主要思想是，类似斜率优化，先找下凸壳，再找上凸壳，最后拼起来就是凸包了。

我们先定义几个待会儿会用的函数：

• 斜率比较

  inline bool slope_judge (node a, node b, node c) {
  	return (a.y - b.y) * (b.x - c.x) < (a.x - b.x) * (b.y - c.y);
  }
  

  其中(b)点因为找凸包的时候要用两遍，就写一个了

  这个函数用来比较直线(AB)与直线(BC)的斜率，如果(k_{AB}<k_{BC})则返回真，否则返回假

  乘在一起是为了防止被卡精

• 两点之间距离

  inline double dis(node a, node b) {
  	return sqrt((b.y - a.y) * (b.y - a.y) + (b.x - a.x) * (b.x - a.x));
  }
  

  这个暂时没想到可以防掉精的办法……

准备工作做好了，第一步是排个序。

因为题目并不一定有序给出点，所以我们先把点按(x)坐标为第一关键字，(y)坐标为第二关键字排序：

inline bool cmp(node a, node b) {
	return a.x != b.x ? a.x < b.x : a.y < b.y;
}
sort(Point + 1, Point + n + 1, cmp)

我们开个栈维护一下。这里我们先找下凸壳。

什么时候这个点可以被丢掉呢？我们先看一张图：

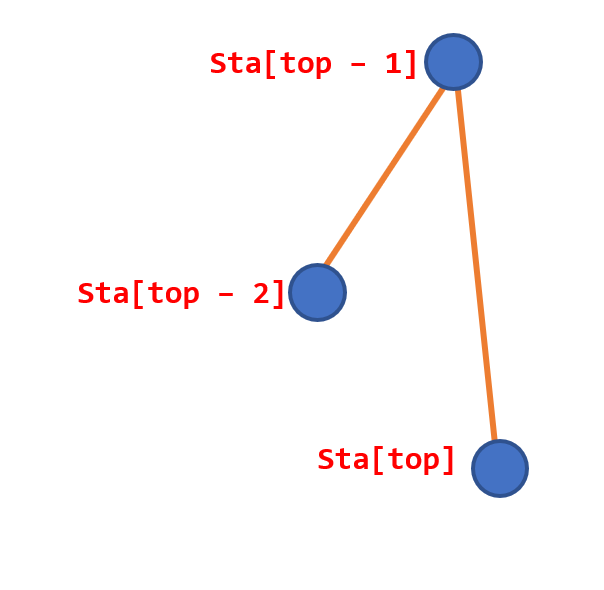
当我们找下凸壳的时候，很显然这个时候应该丢掉(Sta[top - 1])这个点了（可以被(Sta[top - 2])到(Sta[top])的线段框住）

那么可以丢掉一个点的充要条件到底是什么呢？

我们先从成品图来考虑（往上翻翻第一幅图）可以发现整个下凸壳的线段斜率是单调递增的。这是因为如果有上图那样的情况出现，则凹进去那个点一定能被另外两个点的连线框在里面。所以我们维护一个斜率单调的栈，每次遇到不单调的情况就弹出栈内元素，用新的点来替换，直到达到单调或还剩下两个点。

看一下代码：

for (register int i = 1; i <= n; i++) {
	sta[++cnt].x = Point[i].x, sta[cnt].y = Point[i].y;
	while (cnt >= 3 && slope_judge(sta[cnt - 2], sta[cnt - 1], sta[cnt])) {
		sta[cnt - 1] = sta[cnt], --cnt;
	}
}

这样做一遍之后得到的是一个成品的下凸壳。

统计一下答案

for (register int i = 1; i <= cnt - 1; i++) ans += dis(sta[i], sta[i + 1]);

然后我们反过来做一遍就是一个上凸壳了~上凸壳相反，维护的是一个斜率单调递减的单调栈。

注意找上凸壳之前(sta)数组要清空，栈顶指针(cnt)要置零。

看一下完整代码

#include <bits/stdc++.h>
#define N (10000 + 5)
#define INF (1000000000 + 9)
using namespace std;
inline int read() {
	int cnt = 0, f = 1; char c = getchar();
	while (!isdigit(c)) {if (c == '-') f = -f; c = getchar();}
	while (isdigit(c)) {cnt = (cnt << 3) + (cnt << 1) + c - '0'; c = getchar();}
	return cnt * f;
}
int n, cnt;
struct node{
	double x, y;
}Point[N], sta[N];
double ans;
inline bool cmp(node a, node b) {
	return a.x != b.x ? a.x < b.x : a.y < b.y;
}
inline bool slope_judge (node a, node b, node c) {
	return (a.y - b.y) * (b.x - c.x) < (a.x - b.x) * (b.y - c.y);
}
inline double dis(node a, node b) {
	return sqrt((b.y - a.y) * (b.y - a.y) + (b.x - a.x) * (b.x - a.x));
}
int main() {
	n = read();
	for (register int i = 1; i <= n; i++)
		scanf("%lf%lf", &Point[i].x, &Point[i].y);
	sort(Point + 1, Point + n + 1, cmp);
	for (register int i = 1; i <= n; i++) {
		sta[++cnt].x = Point[i].x, sta[cnt].y = Point[i].y;
		while (cnt >= 3 && slope_judge(sta[cnt - 2], sta[cnt - 1], sta[cnt])) {
			sta[cnt - 1] = sta[cnt], --cnt;
		}
	}
	for (register int i = 1; i <= cnt - 1; i++) ans += dis(sta[i], sta[i + 1]);
	cnt = 0;
	memset(sta, 0, sizeof(sta));
	for (register int i = 1; i <= n; i++) {
		sta[++cnt].x = Point[i].x, sta[cnt].y = Point[i].y;
		while (cnt >= 3 && !slope_judge(sta[cnt - 2], sta[cnt - 1], sta[cnt])) {
			sta[cnt - 1] = sta[cnt], --cnt;
		}
	}
	for (register int i = 1; i <= cnt - 1; i++) ans += dis(sta[i], sta[i + 1]);
	printf("%.2f", ans);
	return 0;
}