决策单调性

前言

参考博客

我们通常所说的双指针优化并不属于狭义上的决策单调性，那个对函数的性质要求更高

真正的决策单调性可能不止存在一个峰点或谷点

决策单调性的函数一般不是一次函数，不然可以斜率优化

判定

形如(f_i=min/max g_j+val(i,j)),设(f_i)的最优决策点是(p_i)，若(p_{i}le p_{i+1})，则方程满足决策单调性

几何

假如我们把每个点向其他点转移的影响图像化显然不能这样：

(图来自(flashhu)博客)

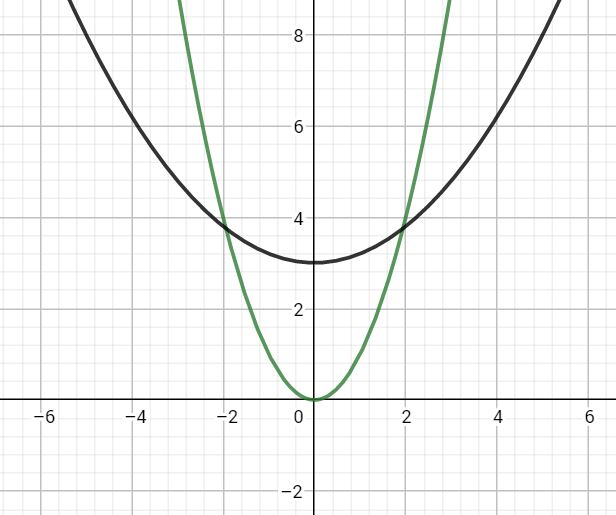
也不能这样

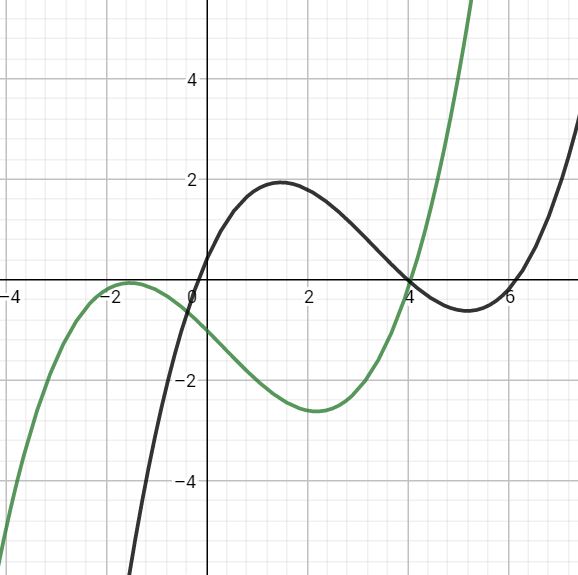
我们发现这样的两个图像，都是某条函数在前一段和后一段更优，显然不满足决策单调性

满足决策单调性的情况应该是某条函数在被另一条函数替代之后永远失去的价值，类似这样

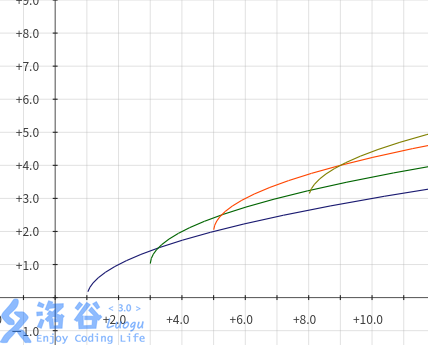
我们需要满足：函数之间可以通过平移得到，函数的导数单调

代数

如果我们的函数满足平行四边形不等式，也满足决策单调性

假设我们的方程求(min),假设(a<b<c<d)

如果(val(a,c)+val(b,d)le val(a,d)+val(b,c))并且(val(b,c)le val(a,d))则说明函数满足决策单调性

还有一个大佬留下的结论，先放在这里：

如果导函数递增、求最大值，或者导函数递减、求最小值，要用单调栈

如果导函数递增、求最小值，或者导函数递减、求最大值，要用单调队列

实现

单调栈/队列

根据上面介绍的几何原理，我们只要维护最靠上/靠下的几个函数拼成曲线

我们可以二分找到当前函数和下一个函数的交接点判断当前函数是否弹出队列，如果当前位置大于函数与下一个函数交接处，说明上一个函数已经没有用了

还要判断队列中元素是否可以被取代，如果队尾前一个元素与当前函数交点比队尾还靠前，说明队尾可以可以被删除

分治

上面的方法必须快速计算(val(x,y))，如果不能快速计算就会导致复杂度退化

我们可以离线分治，(solve(l,r,tl,tr))表示(l,r)的中点位置的决策点在(tl,tr)范围内，我们找到最优决策点的位置(k)

然后分治(solve(l,mid-1,tl,k)),(solve(mid+1,r,k,tr))

例题

[POI2011]Lightning Conductor

先考虑大力化一波式子：

[p_ige a_j-a_i+sqrt{|i-j|} ]

[p_i=max{a_j+sqrt{|i-j|}}-a_i ]

我们可以把绝对值拆成两段，做两次(dp)取最大值

[p_i=max{a_j+sqrt{i-j}}-a_i ]

很像决策单调性式子的一般形式！

考虑一个决策点对其他点的贡献的函数，可以看作(f(x)=sqrt{x-i}+a_i)

发现是一个导数单调递减的幂函数，满足决策单调性

我们可以大力分治，也可以单调队列维护

诗人小G

四边形不等式证明