算法-二叉树前序遍历的思考

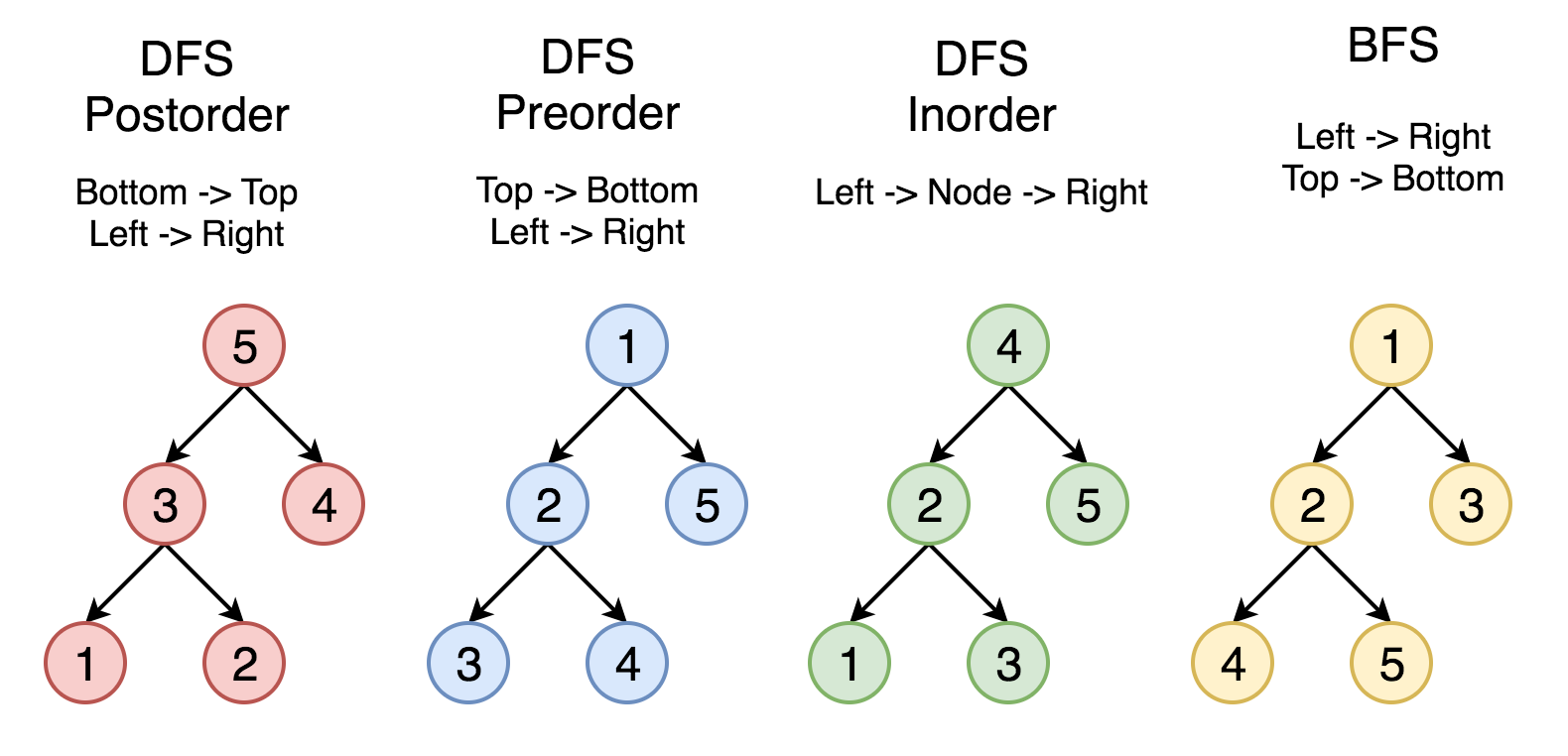
有两种通用的遍历树的策略：

    深度优先搜索（DFS）

    在这个策略中，我们采用深度作为优先级，以便从跟开始一直到达某个确定的叶子，然后再返回根到达另一个分支。

    深度优先搜索策略又可以根据根节点、左孩子和右孩子的相对顺序被细分为前序遍历，中序遍历和后序遍历。

    宽度优先搜索（BFS）

    我们按照高度顺序一层一层的访问整棵树，高层次的节点将会比低层次的节点先被访问到。

作者：LeetCode
链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/er-cha-shu-de-qian-xu-bian-li-by-leetcode/

public:
    vector<int> res;
    vector<int> preorderTraversal(TreeNode* root){
        if(root){
            res.push_back(root -> val);
            preorderTraversal(root -> left);
            preorderTraversal(root -> right);
        }return res; 
    }
};

这个就算公共变量，可以直接用。

我的输入

[1,null,2,3]

我的答案

[1,2,3]

 1 class Solution {
 2 public:
 3     vector<int> preorderTraversal(TreeNode* root){
 4     vector<int> res;
 5         if(root){
 6             res.push_back(root -> val);
 7             preorderTraversal(root -> left);
 8             preorderTraversal(root -> right);
 9         }return res; 
10     }
11 };

这个res就是局部变量，输入0,null,1,2 输出就是1，而没有其他值。

这属于程序接口问题，preorderTraversal(TreeNode* root){}相当于一个函数，里面的内容算是临时变量，所以只有一个值出来。

再来改进
首先 遍历可以不用递归 ( 比如莫里斯遍历 )这样能提高效率
如果用递归可以搞两个函数 外部函数声明临时变量 然后内部函数每次往这个临时变量里面push 这样就行了

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> ret;
    vector<int> preorderTraversal(TreeNode* root) {
        pre_travel(root);
        return ret;
    }
    void pre_travel(TreeNode* root)
    {
        if(root)//当前结点非空
        {
            ret.push_back(root->val);//访问根节点
            pre_travel(root->left);//递归左子树
            pre_travel(root->right);//递归右子树
        }
    }
};

 再就是，递归的本质其实可以理解成栈。    递归的本质就是压栈，了解递归本质后就完全可以按照递归的思路来迭代。
    怎么压，压什么？压的当然是待执行的内容，后面的语句先进栈，所以进栈顺序就决定了前中后序。

我们需要一个标志区分每个递归调用栈，这里使用nullptr来表示。
具体直接看注释，可以参考文章最后“和递归写法的对比”。先序遍历看懂了，中序和后序也就秒懂。

链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/solution/miao-sha-quan-chang-ba-hou-lang-by-sonp/

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;  //保存结果
        stack<TreeNode*> call;  //调用栈
        if(root!=nullptr) call.push(root);  //首先介入root节点
        while(!call.empty()){
            TreeNode *t = call.top();
            call.pop();  //访问过的节点弹出
            if(t!=nullptr){
                if(t->right) call.push(t->right);  //右节点先压栈，最后处理
                if(t->left) call.push(t->left);
                call.push(t);  //当前节点重新压栈（留着以后处理），因为先序遍历所以最后压栈
                call.push(nullptr);  //在当前节点之前加入一个空节点表示已经访问过了
            }else{  //空节点表示之前已经访问过了，现在需要处理除了递归之外的内容
                res.push_back(call.top()->val);  //call.top()是nullptr之前压栈的一个节点，也就是上面call.push(t)中的那个t
                call.pop();  //处理完了，第二次弹出节点（彻底从栈中移除）
            }
        }
        return res;
    }
};        //先序遍历

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> call;
        if(root!=nullptr) call.push(root);
        while(!call.empty()){
            TreeNode *t = call.top();
            call.pop();
            if(t!=nullptr){
                call.push(t);  //在右节点之前重新插入该节点，以便在最后处理（访问值）
                call.push(nullptr); //nullptr跟随t插入，标识已经访问过，还没有被处理
                if(t->right) call.push(t->right);
                if(t->left) call.push(t->left);
            }else{
                res.push_back(call.top()->val);
                call.pop();
            }
        }
        return res;   
    }
};

后序遍历

void dfs(t){ //进入函数表示“访问过”，将t从栈中弹出

    dfs(t->left);   //因为要访问t->left, 所以我先把函数中下面的信息都存到栈里。
                //依次call.push(t->right), call.push(t)【t第二次入栈】, call.push(nullptr)【标识t二次入栈】, call.push(t->left)。
                //此时t并没有被处理（卖萌）。栈顶是t->left, 所以现在进入t->left的递归中。

    //res.push_back(t->val)
    t.卖萌();   //t->left 处理完了，t->left被彻底弹出栈。
                //此时栈顶是nullptr, 表示t是已经访问过的。那么我现在需要真正的处理t了（即，执行卖萌操作）。
                //卖萌结束后，t 就被彻底弹出栈了。
    

    dfs(t->right); 
}         //中序遍历