根据二项式定理有


得

这个公式配合容斥可以解决区间互质问题。
在考虑两个区间互质的情况之前我们先考虑它的一个子问题,一个数x与一个区间[l,r]的互质问题。
处理这个问题,最简单的方法肯定是遍历区间,复杂度为O(n),n为区间长度,显然太慢。
这时我们可以逆向思维,转换问题,我们可以考虑求不互质的个数,然后再用全部个数减去不互质的个数。
不互质也就是说,有公共的因子,如果把问题转换成求同有某个因子的数量,那就好处理, 比如如果计算都有因子2,设区间为[l,r],那我们只要计算1~r的个数减去1~l-1的个数,也非常好算,只要r/2-(l-1)/2 就可以计算出区间[l,r]中有因子2的数字的数量(这里的除法若无特殊说明都为整数除法,即向下取整)。
这样我们就可以把数x进行因数分解,然后对每一个因数去计算区间中有几个数同时有这个因数,累加到sum[i](i为当前这个因数中有几个质因子),这样我们就把区间中的数分类到了,几个集合中,数sun[i],就表示区间中与x共有i个质因子的数的数量,当然这些集合并不是区间的一个划分,因为这几个集合是有共有部分的,这时我们就用到我们上面推出的公式了。
假设区间中一个数y与x的共有质因子数量为1,那在sum[1]中会对他算一次,sum[2]中会对它算0次.
如果共有质因子的数量为2,那sun[1]中会对它算2次(比如y有质因子(2,3),x有质因子(2,3,5),这时取2,计算了一次,取3又计算了一次,所以是两次),sum[2]对他计算1次。
同样,如果共有质因子的数量为2,那sun[1]中会对它算3次,sum[2]对他计算3次(3个中选2个),sum[3]是一次,sum[4]零次。
由此我们可以列一个表格
1 2 3 4 5
1 1 0 0 0 0
2 2 1 0 0 0
3 3 3 1 0 0
4 4 6 4 1 0
5 5 12 12 5 1
很明显,第i行第j列的值就是C(i,j),我们要通过容斥将每一列通过四则运算得出一列全为1的数,这时利用到上面的公式:

根据公式,实际上我们从行第一个开始向后,加减加减的累和,最后的结果就是1.
所以,得出数x对区间[l,r]不互质的个数为

所以,x对区间[l,r]的互质个数为
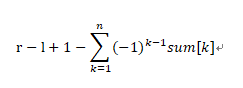
既然已经可以算出x对区间[l,r]的个数了,那两个区间的同样,遍历一遍另一个区间然后按同样的方法就可以计算得出。