前置知识:
容斥原理(可参考https://www.cnblogs.com/komet/p/15156521.html),
互质概念,
基础数学。
欧拉函数 φ(n) 定义为对正整数n,小于n的正整数中与n互质的数的数目。
通项公式为:
![]() 公式1
公式1
先不考虑欧拉函数具体是什么,我们先考虑它的定义——小于n的正整数中与n互质的数的数目。给你一个这样的问题你该如何解决?
最朴素的想法肯定是,一一判断,枚举1到n,每次枚举就判断目前枚举的数字i和n是否互质,即gcd是否为1,但这样就太慢了,算法的复杂度为O(nlogn),或者先预处理出n的质因子,判断时用是否整除判断,复杂度或许会更好些,但都还是太慢了。
看过我博客的人就会发现,这问题明显是区间互质问题的一个子问题,用容斥原理就可以在能O(logn)内解决,准确的说应该是O(k^2)的复杂度,k为n的质因子个数。
公式如下: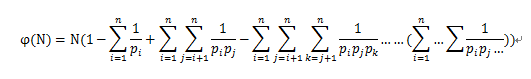 公式2
公式2
(n为N质因子的数量,p1~pn为质因子,该公式的证明由上面给出的我上篇随笔得出,读者也可以自己独立思考该公式。)
简单的说,该公式就是N乘质因子的所有组合的倒数的偶数和与负数的奇数和。
如n为3时该公式为,n*(1-(1/p1+1/p2+1/p3)+(1/p1p2+1/p1p3+1/p2p3)-(1/p1p2p3)) (p 为质因子)
这时回头看看欧拉函数,是不是很相似。
由于上面那个公式化简起来比较麻烦,我们先来考虑一个简单的化简
有式子1+ a+b+c+ab+ac+ad+abc
提取公因式a
有 a(1+b+c+bc)+1+b+c+bc
提取公因式1+b+c+bc
有(1+a)(1+b+c+bc)
提取公因式b
有 (1+b)(1+c+b(1+c))
提取公因式1+c
有 (1+a)(1+b)(1+c)=1+ a+b+c+ab+ac+ad+abc
若a=-1/p1 , b=-1/p2 , c=-1/p3
则有,(1-1/p1)(1-1/p2)(1-1/p3)=1-(1/p1+1/p2+1/p3)+(1/p1p2+1/p1p3+1/p2p3)-(1/p1p2p3)
推广:
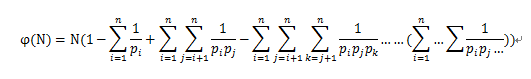
同N(1-1/p1)(1-1/p2)(1-1/p3)...(1-1/pn)
即![]()