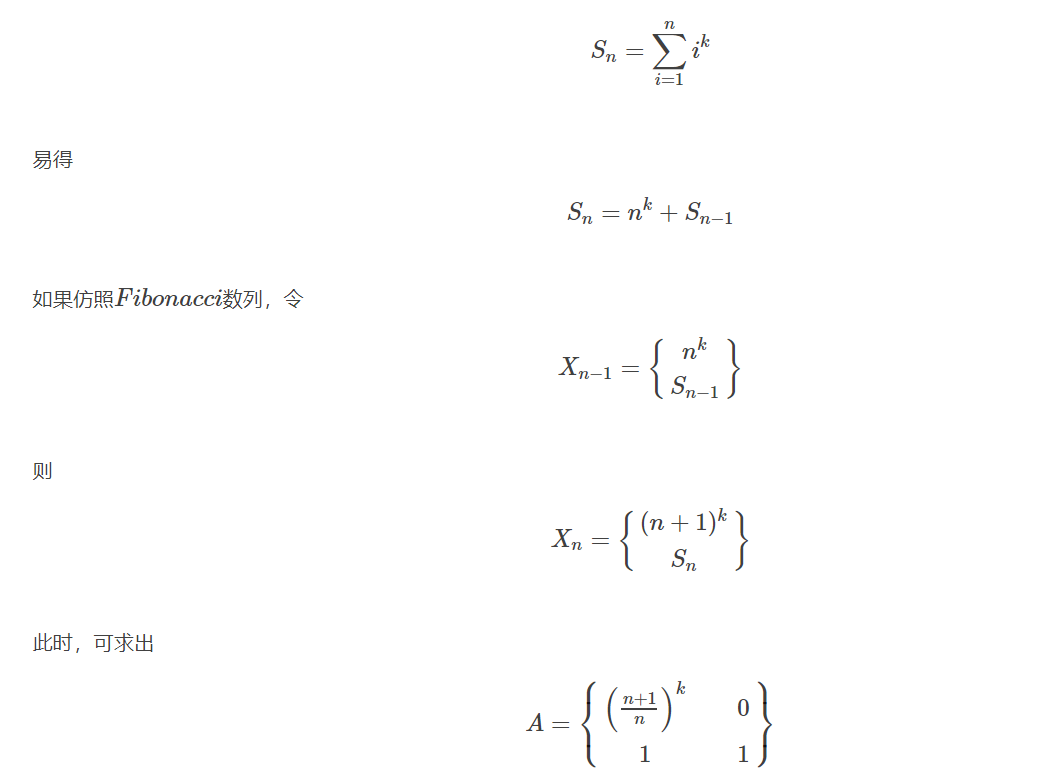矩阵快速幂

基础知识：线性代数

一、

先以斐波那契入手——F(n)=F(n-1)+F(n-2)

我们要先确定目标矩阵

| F(n)    |   

| F(n-1) |    这个就是目标矩阵（设为X(n)）

之后我们就要去寻找那个参数矩阵（矩阵里面的值都可以看成是已知的，在计算过程中其中不含未知数）

先思考我们如何去寻找目标矩阵的第一位F(n)的值，由斐波那契公式我们就知道这个参数矩阵A的第一行的值一定都是1，因为按照线性代数矩阵相乘原则A*X，就是A矩阵的第n行的每一项乘与X矩阵的第n列的每一项

相乘之后就是F(n)=F(n-1)+F(n-2)

那么参数矩阵第二列相信也能推出来，那么最后参数矩阵就是：

| 1  1 |  

| 0  1 |

整理一下：

| F(n-1) |            *           | 1  1 |          =         | F(n)    |

| F(n-2) |                        | 1  0 |                     | F(n-1) |

二、

如果把式子换成 F(n)=aF(n-1)+bF(n-2)，那么就只需要把第一行换成字母a、b即可（a、b可不是未知数）

参数矩阵

| a  b |         

| 1  0 |

其他的都不变就可以

三、利用二项是展开求解 参考博客：https://blog.csdn.net/u012061345/article/details/52224623