网络流算法

原文博客：https://blog.csdn.net/stevensonson/article/details/79177530

网络流图是一张只有一个源点和汇点的有向图，而最大流就是求源点到汇点间的最大水流量，下图的问题就是一个最基本，经典的最大流问题

 二.流量，容量和可行流

对于弧(u,v)来说，流量就是其上流过的水量(我们通常用f(u,v)表示)，而容量就是其上可流过的最大水量(我们通常用c(u,v)表示)，只要满足f(u,v)<=c(u,v)，我们就称流量f(u,v)是可行流(对于最大流问题而言，所有管道上的流量必须都是可行流)。

三.增广路

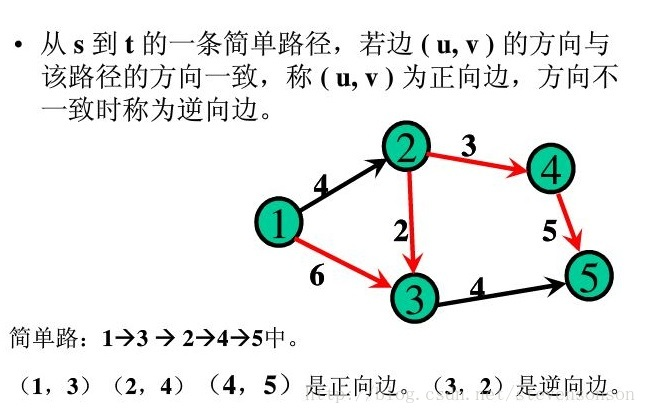
 如果一条路上的所有边均满足:正向边: f(u,v)< c(u,v) ——– 反向边：f(u,v)> 0则我们称这条路径为一条增广路径，简称增广路。

好了，弄懂了一些定义，接下来就可以介绍著名的Ford-Fulkerson算法了。

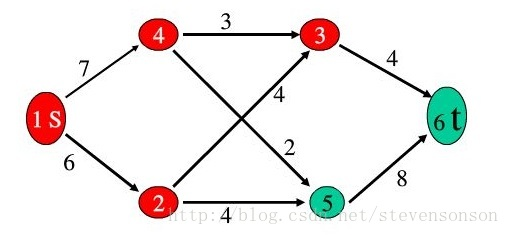
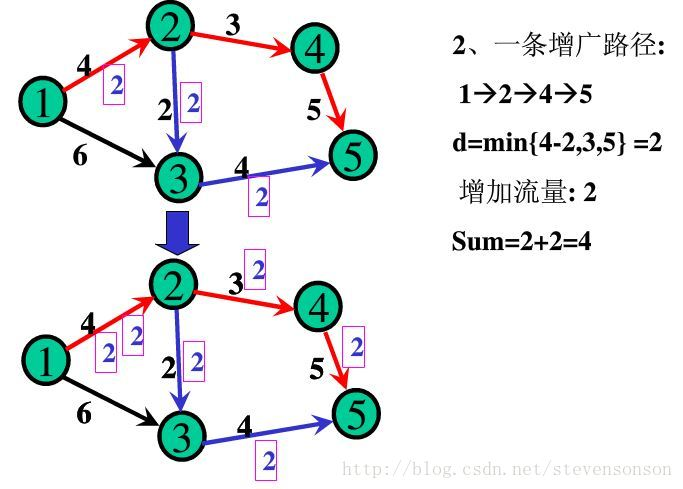
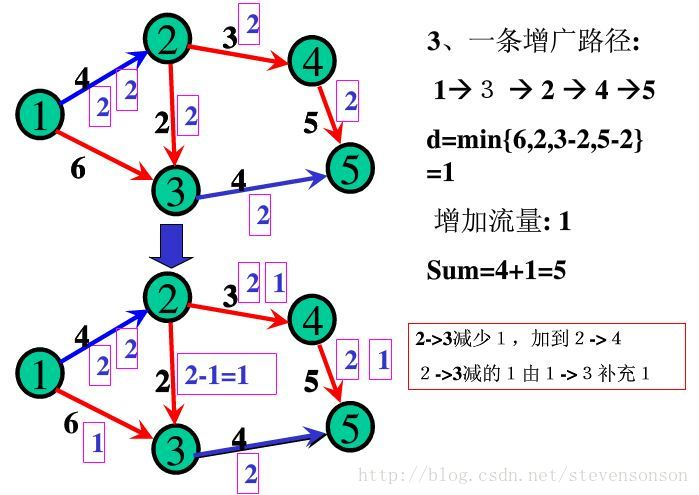
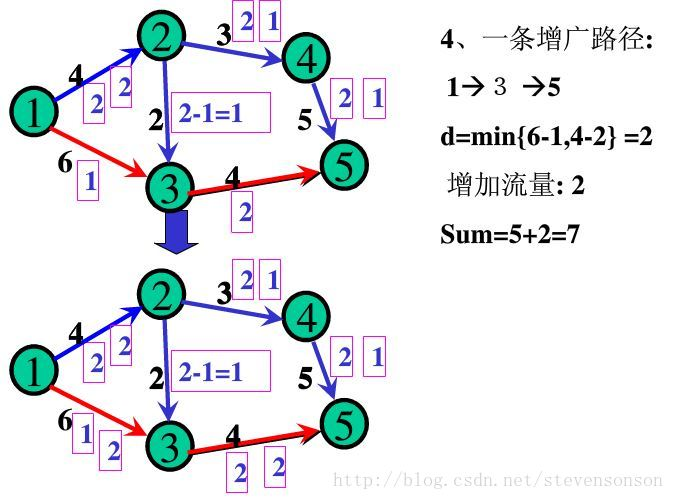
 如图所示，如果我们每次都找出一条增广路，只要这条增广路经过汇点，那说明此时水流还可以增加，增加的量为d(d=min(d,c(u,v)-f(u,v))或d=min(d,f(u,v)))。

我们可以这样理解：对于每一条正向边，他能添加的最大水流为c(u,v)-f(u,v)。而对于反向边来说，当正向边上的水流增多时，反向边自身的反向水流会减少，而其能减少的最多水量为f(u,v)。由于要保证添加水流之后，所有的f(u,v)都是可行流，所以我们取最小值。

增加之后，我们要更新流量，每条正向边+d,每条反向边-d即可。

既然这样，我们的思路就是：

1.找出一条增广路径 ——2.修改其上点的值——3.继续重复1，直至找不出增广路。则此时源点的汇出量即为所求的最大流。

 

 

 

 

 

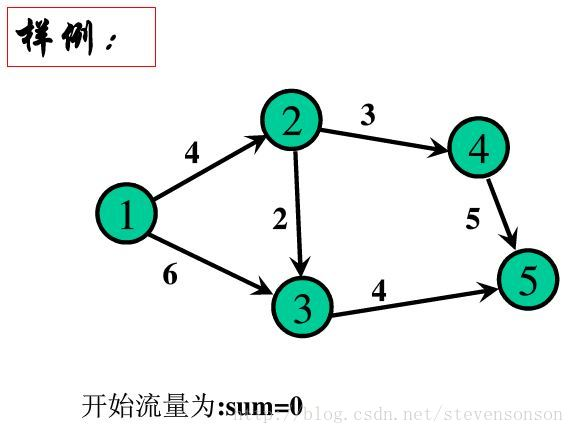
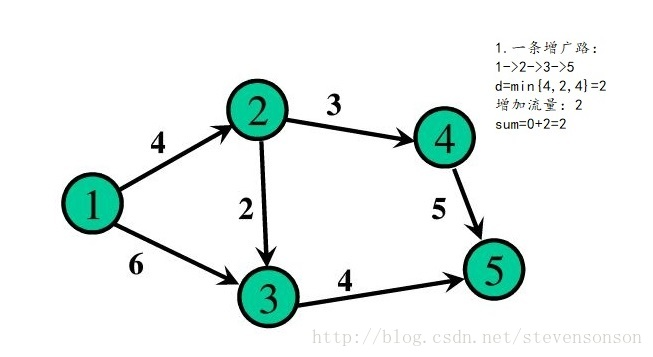
 我这里就不贴这个算法的代码了，想看的可以去原文上面看。在这里我贴一下DINIC算法代码模板：

DINIC算法

Dinic算法是网络流最大流的优化算法之一，每一步对原图进行分层，然后用DFS求增广路。时间复杂度是O(n^2*m)，Dinic算法最多被分为n个阶段，每个阶段包括建层次网络和寻找增广路两部分。

Dinic算法的思想是分阶段地在层次网络中增广。它与最短增广路算法不同之处是：最短增广路每个阶段执行完一次BFS增广后，要重新启动BFS从源点st开始寻找另一条增广路;而在Dinic算法中，只需一次BFS过程就可以实现多次增广。

简单来说，分为下面几步：

　　1.在剩余网络中查找是否存在从S到T的路径，同时建分层图。
　　　　分层图的层数其实就是S到i这个点需要几步。
　　2.沿着分层图多路增广。
　　　　增广时一定要满足dis[j]=dis[i]+1。
　　3.直到没有S到T的路径是结束算法。

下面代码的题目解析可以到这里看https://www.cnblogs.com/kongbursi-2292702937/p/11782283.html

代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=10000;
const int INF=0x3f3f3f3f;
int head[maxn],cnt,st,en,dis[maxn],cur[maxn];
struct edge
{
    int v,next,c,flow;
}e[maxn];
void add_edge(int x,int y,int z)
{
    e[cnt].v=y;
    e[cnt].c=z;
    e[cnt].flow=0;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
bool bfs()
{
    memset(dis,0,sizeof(dis));
    dis[st]=1;
    queue<int>r;
    r.push(st);
    while(!r.empty())
    {
        int x=r.front();
        r.pop();
        for(int i=head[x];i!=-1;i=e[i].next)
        {
            int v=e[i].v;
            if(!dis[v] && e[i].c>e[i].flow)
            {
                dis[v]=dis[x]+1;
                r.push(v);
            }
        }
    }
    return dis[en];
}
int dinic(int s,int limit)
{
    if(s==en || !limit) return limit;
    int ans=0;
    for(int &i=cur[s];i!=-1;i=e[i].next)
    {
        int v=e[i].v,feed;
        if(dis[v]!=dis[s]+1) continue;
        feed=dinic(v,min(limit,e[i].c-e[i].flow));
        if(feed)
        {
            e[i].flow+=feed;
            e[i^1].flow-=feed;
            limit-=feed;
            ans+=feed;
            if(limit==0) break;
        }
    }
    if(!ans) dis[s]=-1;
    return ans;
}
int main()
{
    memset(head,-1,sizeof(head));
    //从这开始都是建图
    int n,f,d;
    scanf("%d%d%d",&n,&f,&d);
    st=0;
    en=2*n+f+d+1;
    for(int i=1;i<=f;++i)
    {
        add_edge(st,2*n+i,1);
        add_edge(2*n+i,st,0);
    }
    for(int i=1;i<=d;++i)
    {
        add_edge(2*n+f+i,en,1);
        add_edge(en,2*n+f+i,0);
    }
    for(int i=1;i<=n;++i)
    {
        add_edge(i,n+i,1);
        add_edge(n+i,i,0);
        int sum1,sum2;
        scanf("%d%d",&sum1,&sum2);
        int x;
        for(int j=0;j<sum1;++j)
        {
            scanf("%d",&x);
            add_edge(x+2*n,i,1);
            add_edge(i,x+2*n,0);
        }
        for(int j=0;j<sum2;++j)
        {
            scanf("%d",&x);
            add_edge(n+i,x+f+2*n,1);
            add_edge(x+f+2*n,n+i,0);
        }
    }
    //到这建图结束
    
    int ans=0;
    while(bfs())
    {
        for(int i=0;i<=en;i++)
            cur[i]=head[i];
        ans+=dinic(st,INF);
    }
    printf("%d
",ans);
    return 0;
}