zoukankan      html  css  js  c++  java

  • Gym

    比赛链接：https://vjudge.net/contest/409725#problem

    题面点此处进入

    Gym - 102062A

    题意：

    就是说比赛一共发a+b+c+d个牌子，现在不带上主人公已经有N个人了，问你带上主人公这场比赛发牌子的数量到不到总人数一半

    代码：

     1 /*
 2  * @Author: hesorchen
 3  * @Date: 2020-11-21 17:26:54
 4  * @LastEditTime: 2020-11-25 13:17:10
 5  * @Description: 栽种绝处的花
 6  */
 7 #include <bits/stdc++.h>
 8 using namespace std;
 9 
10 int main()
11 {
12     int t;
13     scanf("%d", &t);
14     while (t--)
15     {
16         int n, a, b, c, d;
17         scanf("%d %d %d %d %d", &n, &a, &b, &c, &d);
18         n++;
19         if (n & 1)
20             n++;
21         if (n / 2 <= a + b + c + d)
22             printf("Yes
");
23         else
24             printf("No
");
25     }
26     return 0;
27 }
    View Code

    Gym - 102062B

    题意：

    给你圆的质量和密度。让你求圆的表面积

    题解：

    S=4*PI*r*r

    代码：

     1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 const double PI = acos(-1);
 5 
 6 int main()
 7 {
 8     int t;
 9     int CA = 0;
10     scanf("%d", &t);
11     while (t--)
12     {
13         double a, b;
14         scanf("%lf %lf", &a, &b);
15         double V = a / b;
16         double r = pow((3.0 * V / (4.0 * PI)), 1.0 / 3);
17         double ans = 4.0 * PI * r * r;
18         printf("Case %d: %.4f
", ++CA, ans);
19     }
20 }
    View Code

    Gym - 102062C 

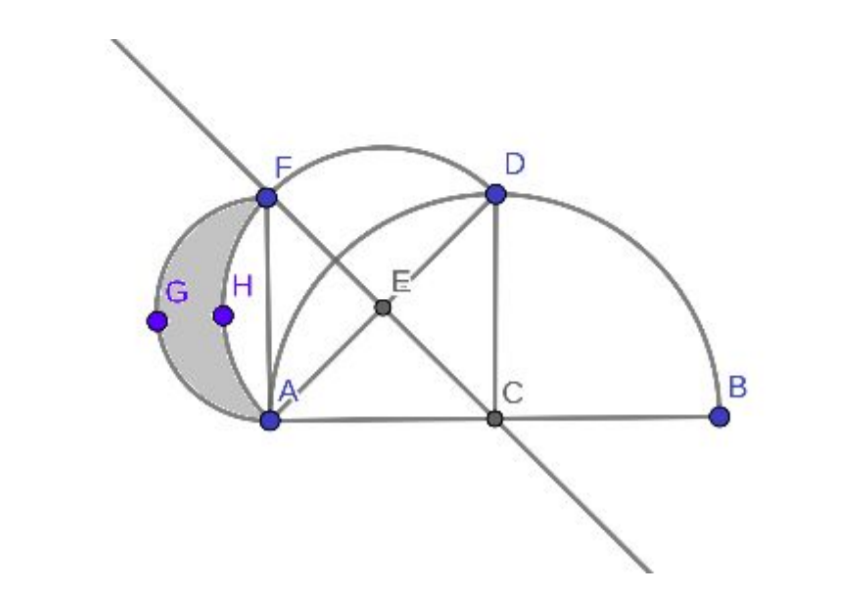
    题意：

    求出阴影部分面积

    题解：

    AGF这个半圆的面积就是半径为r/2的面积的一半

    三角形AEF的面积也可以求出来

    EAHF的面积就是半径为EA的圆面积的四分之一

    前两个减去后面一个就是答案

    代码：

     1 /*
 2  * @Author: hesorchen
 3  * @Date: 2020-11-21 17:26:54
 4  * @LastEditTime: 2020-11-25 14:11:07
 5  * @Description: 栽种绝处的花
 6  */
 7 #include <bits/stdc++.h>
 8 using namespace std;
 9 
10 const double PI = acos(-1);
11 
12 int main()
13 {
14     int t;
15     scanf("%d", &t);
16     int CA = 0;
17     while (t--)
18     {
19         double r;
20         scanf("%lf", &r);
21         double r1 = r / 2;
22         double res1 = PI * r1 * r1 / 2;
23         double res2 = r * r / 4;
24         double r2 = r / (sqrt(2));
25         double res3 = r2 * r2 * PI / 4;
26         double ans = res1 + res2 - res3;
27         printf("Case %d: %.4f
", ++CA, ans);
28     }
29 
30     return 0;
31 }
32 //Case 1: 9
    View Code

    Gym - 102062D 

    题意：

    问你从1开始的第n个是回文数的正整数是几

    题解：

    规律，就是正着输出这个N，再到着输出就是答案

     1 /*
 2  * @Author: hesorchen
 3  * @Date: 2020-11-21 17:26:54
 4  * @LastEditTime: 2020-11-25 13:28:12
 5  * @Description: 栽种绝处的花
 6  */
 7 #include <bits/stdc++.h>
 8 using namespace std;
 9 
10 char s[100090];
11 int main()
12 {
13     int t;
14     scanf("%d", &t);
15     int CA = 0;
16     while (t--)
17     {
18         scanf("%s", s + 1);
19         printf("Case %d: ", ++CA);
20         int len = strlen(s + 1);
21         for (int i = 1; i <= len; i++)
22             printf("%c", s[i]);
23         for (int i = len - 1; i >= 1; i--)
24             printf("%c", s[i]);
25         printf("
");
26     }
27 
28     return 0;
29 }
    View Code

    Gym - 102062E 

    题意：

    在X轴上，你刚开始站在第0位置。每一次你可以向右或者向左移动2d步，且d-=1；你不能到达坐标为负数的位置。问你能不能到达坐标为x的位置。如果可以输出YES并输出你是第几次到达的这个地方。否则输出NO

    题解：

    x>=2d+1都不可能到达。其他的模拟就行

    代码：

     1 /*
 2  * @Author: hesorchen
 3  * @Date: 2020-11-21 17:26:54
 4  * @LastEditTime: 2020-11-25 16:00:22
 5  * @Description: 栽种绝处的花
 6  */
 7 #include <bits/stdc++.h>
 8 using namespace std;
 9 
10 int main()
11 {
12 
13     long long t, CA = 0;
14     scanf("%lld", &t);
15 
16     while (t--)
17     {
18         long long d, x;
19         scanf("%lld %lld", &d, &x);
20         if ((1ll << (d + 1)) <= x)
21         {
22             printf("Case %lld: NO
", ++CA);
23             continue;
24         }
25         else
26         {
27             long long pos = 0, step = 0;
28             while (1)
29             {
30                 if (pos < x)
31                 {
32                     pos += (1ll << d);
33                 }
34                 else if (pos > x)
35                 {
36                     pos -= (1ll << d);
37                 }
38                 else
39                 {
40                     printf("Case %lld: YES %lld
", ++CA, step);
41                     break;
42                 }
43                 // cout << '	' << pos << ' ' << x << endl;
44                 ++step;
45                 --d;
46             }
47         }
48     }
49 
50     return 0;
51 }
52 /**
53  37 6
54 38 5
55 39 6
56 40 3
57 41 6
58 42 5
59 43 6
60 44 4
61 45 6
62 46 5
63 47 6
64 48 2
65 49 6
66 50 5
67 51 6
68 52 4
69 53 6
70 54 5
71 55 6
72 56 3
73 57 6
74 58 5
75 59 6
76 60 4
77 61 6
78 62 5
79 
80  * */
    View Code

    Gym - 102062F

    题意：

    一个数x可以形成一棵树或者一个图，形成过程如下（都是无向边）：

    1、x和它的因子相连（因子排除1和它本身）

    2、x的因子和它的因子相连

    然后判断最后形成的是图还是树。（只有一个点的是树）

    让你输出区间[1,n]内有多少数可以形成树

    题解：

    只要一个数x的质因子数量大于2就不是树

    因为如果x=a*b*c（a、b、c都是质因子），那么x也可以被a*b整除，那么a*b就可以和a、b相连，那这就形成环了

    代码：

     1 /*
 2  * @Author: hesorchen
 3  * @Date: 2020-11-21 17:26:54
 4  * @LastEditTime: 2020-11-25 16:47:54
 5  * @Description: 栽种绝处的花
 6  */
 7 #include <bits/stdc++.h>
 8 using namespace std;
 9 int sum[1000010];
10 
11 int f(int x)
12 {
13     int ans = 0;
14     for (int i = 2; i <= sqrt(x); i++)
15     {
16         if (x % i == 0)
17         {
18             while (x % i == 0)
19             {
20                 ans++;
21                 x /= i;
22             }
23         }
24     }
25     if (x > 1)
26         ans++;
27     if (ans > 2)
28         return 0;
29     return 1;
30 }
31 void init()
32 {
33     sum[1] = 1;
34     for (int i = 2; i <= 1000000; i++)
35     {
36         if (f(i))
37             sum[i] = 1;
38     }
39     for (int i = 2; i <= 1000000; i++)
40         sum[i] += sum[i - 1];
41 }
42 int main()
43 {
44     init();
45     int n, t, id = 0;
46     scanf("%d", &t);
47     while (t--)
48     {
49         scanf("%d", &n);
50         int x = sum[n];
51         int y = __gcd(x, n);
52         n /= y, x /= y;
53         printf("Case %d: %d/%d
", ++id, x, n);
54     }
55     return 0;
56 }
57 /**
58  37 6
59 38 5
60 39 6
61 40 3
62 41 6
63 42 5
64 43 6
65 44 4
66 45 6
67 46 5
68 47 6
69 48 2
70 49 6
71 50 5
72 51 6
73 52 4
74 53 6
75 54 5
76 55 6
77 56 3
78 57 6
79 58 5
80 59 6
81 60 4
82 61 6
83 62 5
84 
85  * */
    View Code

    Gym - 102062G

    题意：

    给你一个字符串s，对于s的所有子串，我们需要计算全部子串的贡献，加起来取模1e9+7输出就可以

    例如给你一个字符串str，他的贡献就是∑len(str)*str[i] (1<=i<=len(str))

    题解：

    暴力T定了，正解是找规律，找字符串每一个位置计算了多少次，设一个位置计算次数为wi

    最后求和∑wi*s[i]输出就是答案

    代码：

     1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 #define mod 1000000007
 5 char s[100010];
 6 int main()
 7 {
 8     long long t;
 9     scanf("%lld", &t);
10     long long CA = 0;
11     while (t--)
12     {
13         long long n, ans = 0, res = 0;
14         scanf("%lld", &n);
15         scanf("%s", s + 1);
16         for (long long i = 1; i <= n; i++)
17         {
18             res += (n - i + 1) * ((n - i + 1) + 1) / 2;
19             res -= (i - 1) * i / 2;
20             ans = (ans + (s[i] * res) % mod) % mod;
21         }
22         printf("Case %lld: %lld
", ++CA, ans);
23     }
24 }
    View Code

    Gym - 102062H 

    题意：

    计算字符串忍耐度程序如下：

    int tolerance(char Txt[], int len){
int sum=0;
for(int i=1, j=len; i<j; i++, j--){
sum=sum+abs(Txt[j]-Txt[i]);
}
return sum;
}

    题目给你一个字符串s，对于每次询问L、R、X

    就是计算s字符串的的子字符串s[L,R]。求这一部分的忍耐度，如果大于x就去掉头部和尾部各一个字符，再次计算，重复这个过程

    输出的话就是输出最后子字符串的长度

    题解：

    模拟

    预处理一下s字符串的所有子字符串的忍耐度

    之后二分最后答案长度就可以了

    代码：

     1 #include <bits/stdc++.h>
 2 using namespace std;
 3 const int maxn = 6e3 + 10;
 4 #define mod 1000000007
 5 
 6 char s[maxn];
 7 int w[maxn][maxn];
 8 int main()
 9 {
10     int t, n;
11     scanf("%d", &t);
12     while (t--)
13     {
14         scanf("%s", s + 1);
15         n = strlen(s + 1);
16         for (int i = 1; i <= n; ++i)
17         {
18             w[i][i] = 0;
19             for (int j = 1; j <= n; ++j)
20             {
21                 int start = i - j;
22                 int last = i + j;
23                 if (i - j >= 1 && i + j <= n)
24                 {
25                     w[i - j][i + j] = w[start + 1][last - 1] + abs(s[last] - s[start]);
26                 }
27                 else
28                     break;
29             }
30         }
31         for (int i = 1; i <= n; ++i)
32         {
33             for (int j = 1; j <= n; ++j)
34             {
35                 int start = i - j + 1;
36                 int last = i + j;
37                 if (start >= 1 && last <= n)
38                 {
39                     if (j == 1)
40                         w[start][last] = abs(s[last] - s[start]);
41                     else
42 
43                         w[start][last] = w[start + 1][last - 1] + abs(s[last] - s[start]);
44                 }
45                 else
46                     break;
47             }
48         }
49         int m ;
50         scanf("%d", &m);
51         while (m--)
52         {
53             int x, y, z;
54             scanf("%d%d%d", &x, &y, &z);
55             int l = 0, r = (y - x + 1) / 2, ans = 0;
56             while (l <= r)
57             {
58                 int mid = (l + r) >> 1;
59                 if (y - mid < x + mid)
60                 {
61                     ans = mid;
62                     break;
63                 }
64                 if (w[x + mid][y - mid] <= z)
65                 {
66                     ans = mid;
67                     r = mid - 1;
68                 }
69                 else
70                     l = mid + 1;
71             }
72             // cout<<ans<<endl;
73             printf("%d
", (y - x + 1) - ans * 2);
74         }
75     }
76     return 0;
77 }
78 /*
79 
80 
81  abcde
82 w[2][2]=0;w[1][3]
83 w[3][3]=0;w[2][4]/w[1][5]
84 w[4][4]=0;w[3][5]/w[2][6]/w[1][7]
85 
86 w[3][4] w[2][5]
87 w[4][5] w[3][6]
88 
89 
90 */
    View Code
  • 相关阅读:
    [LeetCode]Add Two Numbers
    [LeetCode]Longest SubString Without Repeating Characters
    [LeetCode]Median of Two Sorted Arrays
    [LeetCode]Two Sum
    动态规划
    [shell编程]一个简单的脚本
    一些linux的问题
    核稀疏表示分类（KSRC）
    conda 按照指定源下载python包
    python 保留两位小数
  • 原文地址：https://www.cnblogs.com/kongbursi-2292702937/p/14046878.html
Copyright © 2011-2022 走看看