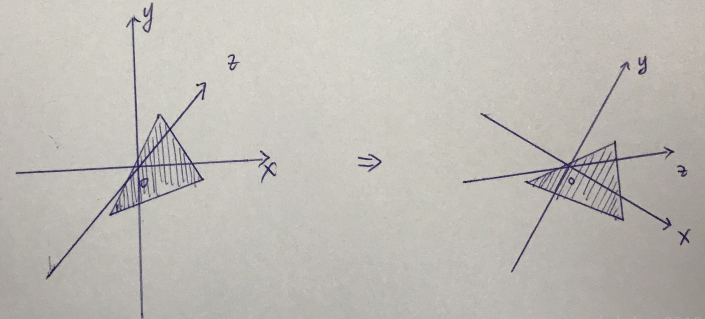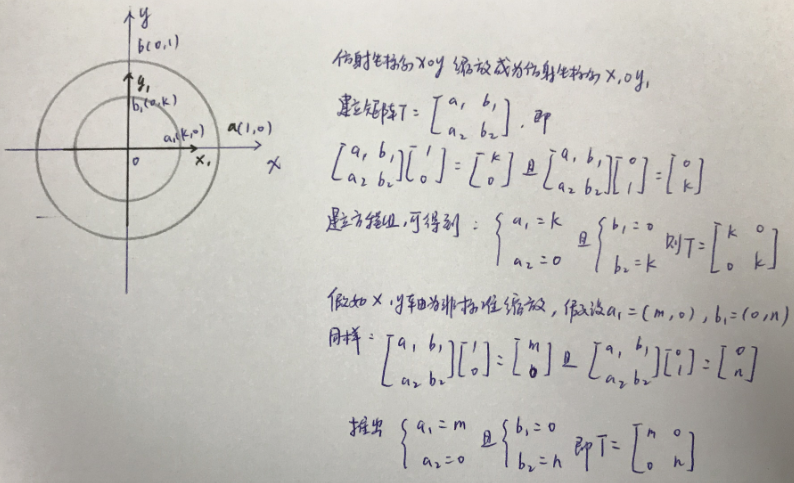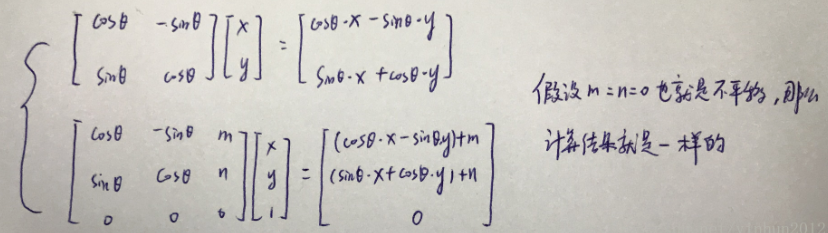矩阵是什么我就不必介绍了,如果一个n*m(n行m列)的矩阵和a*b(a行b列)矩阵要相乘,那么必须满足m==a这个条件。相加的话需要满足n==a && m==b条件。
这里我们先介绍一些关键词:
1、线性相关:
β = m*α1 + n*α2
数学称β可以由向量组{α1,α2}线性表示,同时称β,α1,α2为线性相关。
ps:反过来就是说假如β不能由{α1,α2}线性表示,则称β,α1,α2为线性无关。
2、向量空间和子空间
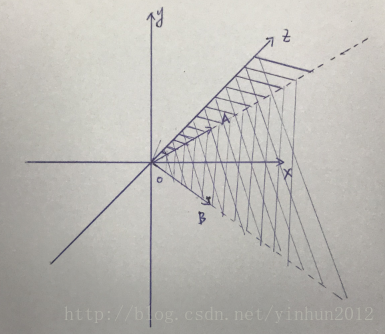
在OA,OB,OZ张成的立体空间中任意向量β = m*OA + n*OB + k*OZ(m,n,k>0),β就是{OA,OB,OZ}的线性表示,当然假如m,n,k为任意实数,就是”张成“了xyz的全部空间了。
这里就有个名词蹦出来了,就是子空间,假如我们把上面m,n,k为任意实数构成的空间叫做S,那么m,n,k>0构成的空间S1就是S的一个子空间。
一个向量组{α1,α2,α3....αn},这个向量组的所有线性组合生成一个向量合集:
{x1*α1 + x2*α2 + x3*α3 ...+xn*αn }且x1,x2...xn属于R
这个向量集合称为Span{α1,α2,α3....αn},称为向量组{α1,α2,α3....αn}张成的向量空间。
3、向量空间的基
对于向量空间S中的一个有序向量组{α1,α2,α3....αn},假如α1,α2,α3....αn线性无关,且任意向量β = x1*α1 + x2*α2 + x3*α3 ...+xn*αn
那么我们称向量组{α1,α2,α3....αn}为向量空间S的一个基,向量组的向量个数称为S的维数,有序实数组{x1,x2,x3...xn}为向量β在基{α1,α2,α3....αn}上的坐标。
4、仿射坐标系
在空间中选取一点做为O原点,从O为起点做任意三个不共面的向量α1,α2,α3,这种方式建立的坐标系叫做仿射坐标系,写成:{O;α1,α2,α3},那么任意一个向量α可以用实数组(x,y,z)来表示,既:α = x*α1+y*α2+z*α3,这里我们称(x,y,z)为向量α的坐标。
ps:仿射坐标系右分为左手和右手坐标系,具体纸面上的区别就是z轴朝纸面内还是纸面外,如果用手来表示就是食指中指拇指成90度夹角,大拇指朝x轴,食指朝y轴,那么中指和z轴的朝向就是区分左右手了。
5、转置矩阵
将矩阵的行列互换得到的新矩阵称为转置矩阵


矩阵可以把一个向量变换成另外一个向量(也就是向量变换)。
6、矢量和向量
矢:空间中的一个直线段,当规定其两个端点中一个为起始点,一个位终止点,这个线段就称为一个矢。
向量:具有同样长度和方向的失的集合称为一个向量,单独的一个矢为向量的一个代表。
7、透视空间
假如我们站在现实世界中的一条很远的马路上,马路尽头在我们眼中就交汇成了一个点,这种现象被称为透视现象,同样的存在这种现象的空间被称为透视空间。透视现象在现实生活中无处不在,计算机视觉中也遵循这个原理。在笛卡尔空间中,两条平行线是永远不会相交的,但是在透视空间中,两条平行线会相交于一点,这是两种空间最大的区别。
首先想像有个绝对不变的坐标系,记为W,然后以W为参照,建立两个坐标系O1和O2, O1的原点在W的(1,1)处,O2的原点在W的(2,2)处。那么W中的一个点P(x,y)在O1中将变为P(x-1,y-1),在O2中将是P(x-2, y-2),这样同一个点P在不同的坐标系下就具有了不同的表示。这会产生一个问题:显然,P点在二维空间的位置是唯一的,是与坐标系无关的,而不同坐标系下的表示看上去体现不了这种无关性。
我们使用的是坐标系这样一个概念,坐标系忽略了坐标原点所具有的重要意义:正是原点标示了该坐标系处于哪个参照位置。如果用矩阵来表示一个二维坐标系,将会是如下形式:
|1 0|
|0 1| ,其中(1 0)T表示一个基矢量,(0 1)T表示另一个基矢量,它们互相垂直,因此能利用它们标记整个二维空间。
(x, y)|1 0| = (x, y)
|0 1|
这就是二维坐标的实际意义。
现在考虑将坐标原点(a,b)也引入到这个矩阵表示中来:
|1 0 |
|0 1 |
|a b |
我们用这个矩阵可以表示二维空间中任意位置的一个坐标系,当然,这个坐标系的基矢量可以不为(0 1)T和(1 0)T,为了和坐标系区分,我们称这种新表示为标架表示。
好,问题来了,如果我们仍然用(x y)来表示点P,那么根据矩阵的乘法规则,我们无法完成其乘法:mx N 的矩阵只能和 N xk的矩阵相乘。解决的办法就是: 给P点添一个尾巴,这个尾巴通常为1:P(x y 1),这就是P的齐次坐标,利用新的齐次坐标和矩阵相乘得到的结果为:
(x+a, y+b),这样同一个点在不同标架下的不同表示最终会得到同一个计算结果,它反映了这样一个事实:同一个点在不同标架下的不同表示其实是等价的,这一点恰恰是使用坐标系无法体现出来的。
显然上面那个 3x2的矩阵和P的齐次表示相乘得到的不是齐次坐标,所以应该将它扩充成3x3的方阵:
|1 0 0|
|0 1 0|
|a b 1|
齐次点具有下列几个性质:
1)如果实数a非零,则(x, y, x, w)和(ax, ay, az, aw)表示同一个点,类似于x/y = (ax)/( ay)。
2)三维空间点(x, y, z)的齐次点坐标为(x, y, z, 1.0),二维平面点(x,y)的齐次坐标为(x, y, 0.0, 1.0)。
3)当w不为零时,齐次点坐标(x, y, z, w)即三维空间点坐标(x/w, y/w, z/w);当w为零时,齐次点(x, y, z, 0.0)表示此点位于某方向的无穷远处。
齐次坐标有什么优点呢?
1.它提供了用矩阵运算把二维、三维甚至高维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法。
2.它可以表示无穷远的点。n+1维的齐次坐标中如果h=0,实际上就表示了n维空间的一个无穷远点。对于齐次坐标[a,b,h],保持a,b不变, 点沿直线 ax+by=0 逐渐走向无穷远处的过程。
第一:许多图形应用涉及到几何变换,主要包括平移、旋转、缩放。以矩阵表达式来计算这些变换时,平移是矩阵相加,旋转和缩放则是矩阵相乘,综合起来可以表示为p' = p *m1+ m2(m1旋转缩放矩阵, m2为平移矩阵, p为原向量 ,p'为变换后的向量)。引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法,表示为p' = p*M的形式。即它提供了用矩阵运算把二维、三维甚至高维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法。
其次,它可以表示无穷远的点。n+1维的齐次坐标中如果h=0,实际上就表示了n维空间的一个无穷远点。对于齐次坐标(a,b,h),保持a,b不变,|V|=(x1*x1,y1*y1,z1*z1)^1/2的过程就表示了标准坐标系中的一个点沿直线 ax+by=0 逐渐走向无穷远处的过程。
实例:
前面我们从理论上理解了图形学中图形的变换过程,具体可以理解为如果要对一个图形A进行变换,那么存在图形A所处的相同原点的仿射空间SpaceA(或者说仿射空间SpaceA中原点处存在一个图形A),这时候我们暂时忽略图形A,只考虑SpaceA经过各种变换最终变换成另一个仿射空间SpaceB(或者说变换后的仿射空间SpaceA与另一个仿射空间SpaceB重合),因为仿射空间SpaceA变换后可能被伸缩或者被旋转同时又移动了,那么仿射空间SpaceA中的图形A同时跟着被变换成了另外的样子,如下图:
想像一下,假设把你自己当作一个“图形”,这时候出现一个任务,就是让躺在床上的你从家里出发去公司坐在办公椅上上班写代码,你应该怎么做呢,首先你要起床(从平躺的向量变成竖着的向量,这就经历了一个人体旋转的过程),然后出发,经过一条长长的街道xxx路(从xxx路的起点路口到xxx路的终点路口,这就经历了一个人体平移的过程),然后拐弯进入yyy路并且继续行走(这就经历了人体旋转加人体平移两个过程),然后进入公司走到办公椅前坐下(从竖着站立状态变成坐下的坐立状态,这可以人为人体进行了形变缩放)。
这么一看,我们对于变换的理解就可以分解为旋转、平移、缩放三个过程。
前面我们对齐次坐标的理解,知道了旋转和缩放这两个过程可以通过矩阵T进行线性变换处理,但是平移却是需要将矩阵T扩充“平移维度”得到矩阵T'才能进行线性变换处理,所以数学上我们处理n维空间的图形变换就要使用n+1维齐次坐标以及n+1行n+1列矩阵来得到。接下来我们就来具体推导二维仿射坐标系下的旋转/平移/缩放。
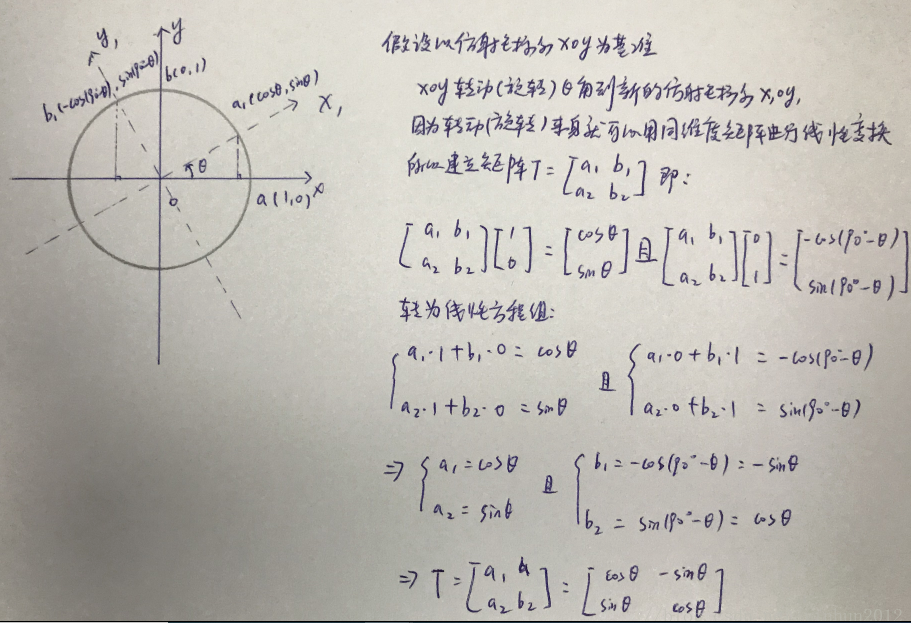
1.矩阵操作仿射坐标系旋转,还是老办法,建立单位圆进行逆时针旋转θ角(三角函数中规定逆时针旋转为正角)的旋转矩阵辅助推导,如下图:
我们通过矩阵T_rotate旋转变换仿射坐标系xoy到x1oy1,矩阵T_rotate的推导也是通过建立线性方程组解方程得到T_rotate的未知数。那么仿射坐标系所“容纳”的原点图形也就跟着变换了。因为旋转变换不需要额外扩充成齐次坐标表示也能进行变换,所以我们忽略“平移维度”。
2.矩阵操作仿射坐标系缩放,建立辅助单位圆,如下图:
上面我们首先推导了标准缩放,也就是xy缩放比例K相同,接下来缩放比例不同x缩放m/y缩放n,依旧是通过建立矩阵T_scale以及转换成线性方程组就很容易得到矩阵T_scale了。
3.矩阵操作仿射坐标系平移,特殊情况来了!前面我们讲过仿射坐标系平移是不能直接进行线性变换的,而需要扩充平移维度进行辅助计算,如下图:
同样的,因为二维平移只有xy轴两个方向,我们建立仿射坐标系观察,同时扩充“平移维度”,建立矩阵T_translate和线性方程组,就能得到我们需要的平移矩阵T_translate。
前面我们推了二维情况下仿射坐标系旋转,缩放,平移的变换矩阵T_rotate,T_scale,T_translate,但是三个矩阵太不规范了,有的是2x2有的是3x3,有的使用了齐次坐标,有的又只使用了普通坐标,这对我们程序中进行计算是非常不友好的。之前我们说了平移变换是通过扩充“平移维度”来处理的,并不影响“旋转维度”和“缩放维度”,同时GPU设计的重要指标之一就是极快速处理4x4及以下的矩阵计算,所以我们通过将T_rotate和T_scale扩充维度到T_translate的行列数,用来统一传入GPU进行处理。
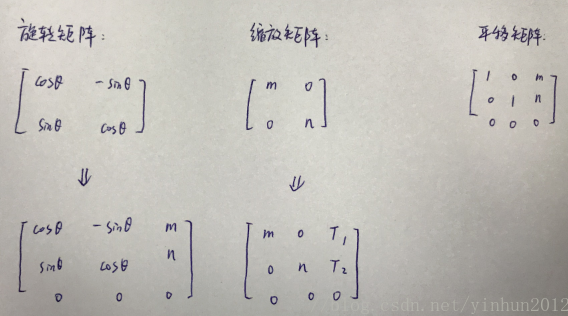
扩充方式如下图:
这里我们只需要将“平移维度”填入“旋转维度”和“缩放维度”就行了,如果不放心的话我们就验证一下扩充后的矩阵的计算结果,如下图:
缩放矩阵同理也可以计算出来结果。
这么一来我们就把旋转平移缩放的变换全部使用齐次坐标和3x3矩阵给统一化了,但是我们还是觉得麻烦,因为我处理一个图形变换居然还需要使用三个矩阵去分别计算,我们能不能直接把这三个矩阵通过什么方法变成一个呢,接下来我们来观察矩阵乘法的性质,继续由简入难。
假设我们有两个2x2的矩阵T1,T2来变换一个2x1的矩阵V(2x1的矩阵也就是一个二维向量),按照平常方法我们肯定就是先使用T1*V变换得到V1,然后再使用T2*V1变换得到V2,整个过程我们记为T2*(T1*V)。我们希望优化中间环节,尽量少的直接将V带入运算,希望变换成(T2*T1)*V,先将T2*T1得到矩阵T3,然后将T3*V变换得到V2,此时我们的问题就变成T2*T1得到的矩阵T3是否起到了T1、T2分别变换V相同的作用。
我们知道矩阵A*矩阵B的规则就是矩阵A的行m与矩阵B的列n的元素分别相乘再相加最终得到的元素放置于结果矩阵C的m行n列中,那么上面的问题矩阵T1*V得到的V1再使用T2*V1得到的结果和T2*T1得到T3*V的结果相同,因为这种矩阵乘法的计算规律在独立出每个行列计算后得到单个元素的分解式符合乘法分配律(c*(a+b) = c*a + c*b)运算然后拆分组合成另外的乘法分配律的组合体,这时候我们必须通过实际运算来观察,因为红色语言的描叙都过于复杂到无法直接心算,如下图:
最后的乘法分配组合经过分解拆分继续组合成乘法分配律组合体。
这时候我们可以将原本的旋转平移缩放三次矩阵操作T_rotate*(T_translate*(T_scale*Vector))变化成T_all(T_all = T_rotate*(T_translate*T_scale)) *Vector,保证Vector经过一个矩阵的一次变换达到目标。
原文链接:https://blog.csdn.net/yinhun2012/article/details/79544205
参考博客:https://blog.csdn.net/yinhun2012/article/details/79566148
https://blog.csdn.net/yinhun2012/article/details/79544205
http://blog.sina.com.cn/s/blog_758521400102voww.html
前面我们从理论上理解了图形学中图形的变换过程,具体可以理解为如果要对一个图形A进行变换,那么存在图形A所处的相同原点的仿射空间SpaceA(或者说仿射空间SpaceA中原点处存在一个图形A),这时候我们暂时忽略图形A,只考虑SpaceA经过各种变换最终变换成另一个仿射空间SpaceB(或者说变换后的仿射空间SpaceA与另一个仿射空间SpaceB重合),因为仿射空间SpaceA变换后可能被伸缩或者被旋转同时又移动了,那么仿射空间SpaceA中的图形A同时跟着被变换成了另外的样子,如下图:
想像一下,假设把你自己当作一个“图形”,这时候出现一个任务,就是让躺在床上的你从家里出发去公司坐在办公椅上上班写代码,你应该怎么做呢,首先你要起床(从平躺的向量变成竖着的向量,这就经历了一个人体旋转的过程),然后出发,经过一条长长的街道xxx路(从xxx路的起点路口到xxx路的终点路口,这就经历了一个人体平移的过程),然后拐弯进入yyy路并且继续行走(这就经历了人体旋转加人体平移两个过程),然后进入公司走到办公椅前坐下(从竖着站立状态变成坐下的坐立状态,这可以人为人体进行了形变缩放)。
这么一看,我们对于变换的理解就可以分解为旋转、平移、缩放三个过程。
前面我们对齐次坐标的理解,知道了旋转和缩放这两个过程可以通过矩阵T进行线性变换处理,但是平移却是需要将矩阵T扩充“平移维度”得到矩阵T'才能进行线性变换处理,所以数学上我们处理n维空间的图形变换就要使用n+1维齐次坐标以及n+1行n+1列矩阵来得到。接下来我们就来具体推导二维仿射坐标系下的旋转/平移/缩放。
1.矩阵操作仿射坐标系旋转,还是老办法,建立单位圆进行逆时针旋转θ角(三角函数中规定逆时针旋转为正角)的旋转矩阵辅助推导,如下图:
我们通过矩阵T_rotate旋转变换仿射坐标系xoy到x1oy1,矩阵T_rotate的推导也是通过建立线性方程组解方程得到T_rotate的未知数。那么仿射坐标系所“容纳”的原点图形也就跟着变换了。因为旋转变换不需要额外扩充成齐次坐标表示也能进行变换,所以我们忽略“平移维度”。
2.矩阵操作仿射坐标系缩放,建立辅助单位圆,如下图:
上面我们首先推导了标准缩放,也就是xy缩放比例K相同,接下来缩放比例不同x缩放m/y缩放n,依旧是通过建立矩阵T_scale以及转换成线性方程组就很容易得到矩阵T_scale了。
3.矩阵操作仿射坐标系平移,特殊情况来了!前面我们讲过仿射坐标系平移是不能直接进行线性变换的,而需要扩充平移维度进行辅助计算,如下图:
同样的,因为二维平移只有xy轴两个方向,我们建立仿射坐标系观察,同时扩充“平移维度”,建立矩阵T_translate和线性方程组,就能得到我们需要的平移矩阵T_translate。
前面我们推了二维情况下仿射坐标系旋转,缩放,平移的变换矩阵T_rotate,T_scale,T_translate,但是三个矩阵太不规范了,有的是2x2有的是3x3,有的使用了齐次坐标,有的又只使用了普通坐标,这对我们程序中进行计算是非常不友好的。之前我们说了平移变换是通过扩充“平移维度”来处理的,并不影响“旋转维度”和“缩放维度”,同时GPU设计的重要指标之一就是极快速处理4x4及以下的矩阵计算,所以我们通过将T_rotate和T_scale扩充维度到T_translate的行列数,用来统一传入GPU进行处理。
扩充方式如下图:
这里我们只需要将“平移维度”填入“旋转维度”和“缩放维度”就行了,如果不放心的话我们就验证一下扩充后的矩阵的计算结果,如下图:
缩放矩阵同理也可以计算出来结果。
这么一来我们就把旋转平移缩放的变换全部使用齐次坐标和3x3矩阵给统一化了,但是我们还是觉得麻烦,因为我处理一个图形变换居然还需要使用三个矩阵去分别计算,我们能不能直接把这三个矩阵通过什么方法变成一个呢,接下来我们来观察矩阵乘法的性质,继续由简入难。
假设我们有两个2x2的矩阵T1,T2来变换一个2x1的矩阵V(2x1的矩阵也就是一个二维向量),按照平常方法我们肯定就是先使用T1*V变换得到V1,然后再使用T2*V1变换得到V2,整个过程我们记为T2*(T1*V)。我们希望优化中间环节,尽量少的直接将V带入运算,希望变换成(T2*T1)*V,先将T2*T1得到矩阵T3,然后将T3*V变换得到V2,此时我们的问题就变成T2*T1得到的矩阵T3是否起到了T1、T2分别变换V相同的作用。
我们知道矩阵A*矩阵B的规则就是矩阵A的行m与矩阵B的列n的元素分别相乘再相加最终得到的元素放置于结果矩阵C的m行n列中,那么上面的问题矩阵T1*V得到的V1再使用T2*V1得到的结果和T2*T1得到T3*V的结果相同,因为这种矩阵乘法的计算规律在独立出每个行列计算后得到单个元素的分解式符合乘法分配律(c*(a+b) = c*a + c*b)运算然后拆分组合成另外的乘法分配律的组合体,这时候我们必须通过实际运算来观察,因为红色语言的描叙都过于复杂到无法直接心算,如下图:
最后的乘法分配组合经过分解拆分继续组合成乘法分配律组合体。
这时候我们可以将原本的旋转平移缩放三次矩阵操作T_rotate*(T_translate*(T_scale*Vector))变化成T_all(T_all = T_rotate*(T_translate*T_scale)) *Vector,保证Vector经过一个矩阵的一次变换达到目标。————————————————版权声明:本文为CSDN博主「羊羊2035」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。原文链接:https://blog.csdn.net/yinhun2012/article/details/79544205