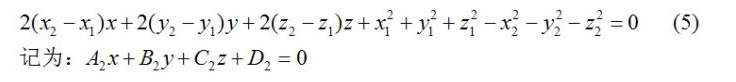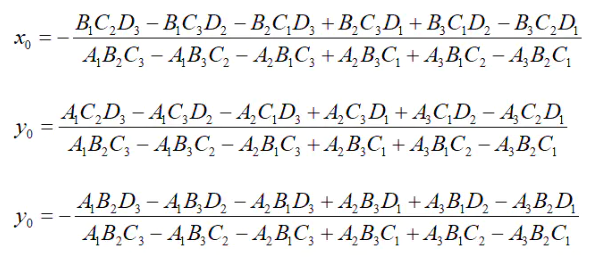转发:https://blog.csdn.net/yanmy2012/article/details/8111600
已知空间三点的坐标为(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),求这三个点所确定的空间圆的圆心坐标和半径。
分析可得约束条件:1、三点共面2、三点到空间圆心坐标的距离相等。
从约束条件可得,4个自由项4个方程可解,可以列出线性代数方程组,即可用消元法求解;
即以下的(1)(2)(3)(4)四个方程组成的线性代数方程组
共面约束:
三点到空间圆心坐标的距离相等约束:
(1) (2)(3)联解可得(5)(6)同时消去R
通过(4)(5)(6)获得关于圆心空间坐标的线性代数方程组
求逆矩阵方法可以看我之前博客:矩阵求逆矩阵
下面给出暴力运算代码:
//x1,y1,z1对应一个点的坐标
//x,y,z,radius是用来返回求解出来的圆心坐标和圆半径
void centerCircle3d(double x1, double y1, double z1, double x2, double y2, double z2, double x3, double y3, double z3, double &x, double &y, double &z,double &radius)
{
double a1 = (y1*z2 - y2*z1 - y1*z3 + y3*z1 + y2*z3 - y3*z2),
b1 = -(x1*z2 - x2*z1 - x1*z3 + x3*z1 + x2*z3 - x3*z2),
c1 = (x1*y2 - x2*y1 - x1*y3 + x3*y1 + x2*y3 - x3*y2),
d1 = -(x1*y2*z3 - x1*y3*z2 - x2*y1*z3 + x2*y3*z1 + x3*y1*z2 - x3*y2*z1);
double a2 = 2 * (x2 - x1),
b2 = 2 * (y2 - y1),
c2 = 2 * (z2 - z1),
d2 = x1*x1 + y1*y1 + z1*z1 - x2*x2 - y2*y2 - z2*z2;
double a3 = 2 * (x3 - x1),
b3 = 2 * (y3 - y1),
c3 = 2 * (z3 - z1),
d3 = x1*x1 + y1*y1 + z1*z1 - x3*x3 - y3*y3 - z3*z3;
x = -(b1*c2*d3 - b1*c3*d2 - b2*c1*d3 + b2*c3*d1 + b3*c1*d2 - b3*c2*d1)
/ (a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1);
y = (a1*c2*d3 - a1*c3*d2 - a2*c1*d3 + a2*c3*d1 + a3*c1*d2 - a3*c2*d1)
/ (a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1);
z = -(a1*b2*d3 - a1*b3*d2 - a2*b1*d3 + a2*b3*d1 + a3*b1*d2 - a3*b2*d1)
/ (a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1);
radius = sqrt((x1 - x)*(x1 - x) + (y1 - y)*(y1 - y) + (z1 - z)*(z1 - z));
}