堆——中位数

·今天考试这题因为小数点问题少了三十分，一开始这题用的暴力做的（就是为了骗分还没骗到┏┛墓┗┓），好吧wsl

·题目内容：

1.Background
虽然CZR数学很烂，但是他还是想证明一下自己的数学能力，今天他
想要表演一下瞬间计算中位数.
2.Description
一开始集合为空，每次有两个操作：
1 x：告诉CZR当前集合中再加入一个数x.
2 ：询问CZR当前集合的中位数是多少.
·题目来源：山东济南集训2019.8考试题二的第三题

·算法：堆顶堆

·算法实现辅助：STL

·算法介绍：

使用两个堆，大根堆维护较小的值，小根堆维护较大的值

即小根堆的堆顶是较大的数中最小的，大根堆的堆顶是较小的数中最大的

将大于大根堆堆顶的数（比所有大根堆中的元素都大）的数放入小根堆，小于等于大根堆堆顶的数（比所有小根堆中的元素都小）的数放入大根堆

那么就保证了所有大根堆中的元素都小于小根堆中的元素

于是我们发现对于大根堆的堆顶元素，有【小根堆的元素个数】个元素比该元素大，【大根堆的元素个数-1】个元素比该元素小；

同理，对于小跟堆的堆顶元素，有【大根堆的元素个数】个元素比该元素小，【小根堆的元素个数-1】个元素比该元素大；

那么维护【大根堆的元素个数】和【小根堆的元素个数】差值不大于1之后，元素个数较多的堆的堆顶元素即为当前中位数；（如果元素个数相同，那么就是两个堆堆顶元素的平均数，本题不会出现这种情况）

根据这两个堆的定义，维护方式也很简单，把元素个数多的堆的堆顶元素取出，放入元素个数少的堆即可。

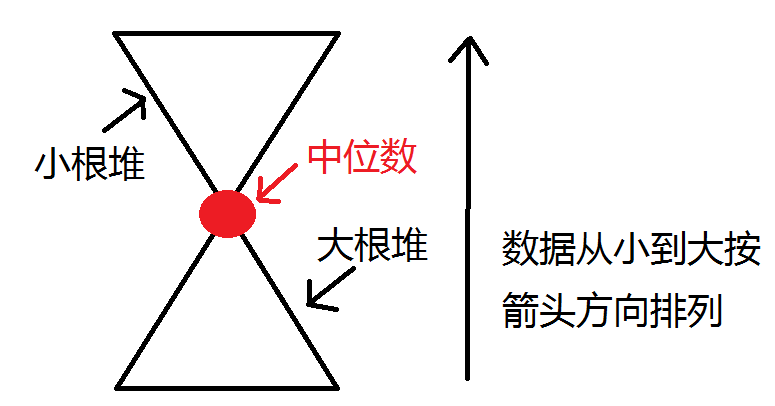
·本题思路：

只要维护两个堆：
一个大根堆，保存的是集合中小的一半的数字；
一个小根堆，保存的是集合中大的一半的数字.
这样子每次加一个数就只要保持堆的大小差距在1之内就可以了.
中位数就是某一个堆顶或者两个堆顶的中位数.

·板子：

#include <cstdio>
#include <queue>

using namespace std;

priority_queue <int, vector<int>, less<int> > mnh;
priority_queue <int, vector<int>, greater<int> > mxh;

inline void insert_mx(int x) {
	mxh.push(x);
}

inline void insert_mn(int x) {
	mnh.push(x);
}

inline int pop_mx() {
	int tmp = mxh.top();
	mxh.pop();
	return tmp;
}

inline int pop_mn() {
	int tmp = mnh.top();
	mnh.pop();
	return tmp;
}

int T;
int op, x;
int ans;
int tot_size;

int main() {
	//freopen("mid.in", "r", stdin);
	//freopen("mid.out", "w", stdout);
	scanf("%d
", &T);
	while (T--) {
		scanf("%d", &op);
		if (op == 1) {
			++tot_size;
			scanf("%d", &x);
			insert_mx(x);
			while (mxh.size() && mnh.size() && mnh.top() > mxh.top()) {
				x = pop_mx(), insert_mn(x);
				x = pop_mn(), insert_mx(x);
			}
			//将大于大根堆堆顶的数（比所有大根堆中的元素都大）的数放入小根堆，
			//小于等于大根堆堆顶的数（比所有小根堆中的元素都小）的数放入大根堆。 
			while (mxh.size() > (tot_size / 2))
				x = pop_mx(), insert_mn(x);
			while (mxh.size() < (tot_size / 2))
				x = pop_mn(), insert_mx(x);
				//保证大根堆大小等于总大小一半.
                //小根堆大小≤大根堆大小+1&&小根堆大小≥大根堆大小
                //想法原因：对于大根堆的堆顶元素，
				          //有【小根堆的元素个数】个元素比该元素大，
				          //【大根堆的元素个数-1】个元素比该元素小； 
		}
		if (op == 2) {
			if (tot_size % 2 == 1) {
				printf("%d
", mnh.top());
			} else {
				ans = mnh.top() + mxh.top();
				if (ans % 2 == 1)
					printf("%d.5
", ans >> 1);
				else
					printf("%d
", ans >> 1);
			}
		}
	}
	//fclose(stdin);
	//fclose(stdout);
	return 0;
}