电路布线

目录
1、问题
2、详细说明
3、代码块

问题
在一块电路板的上下两端分别有n个接线柱。根据电路设计，要求用导线 (i，π(i))，将上端接线柱 i 与下端接线柱 π(i) 相连，
如图，其中 π(i)，1<=i<=n，是(1,2……,n)的一个排列。导线(i，π(i))称为该电路板上的第i条连线。对于任何 1<=i<s<=n，第i条连线和第s条连线相交的充分且必要条件是 π(i) > π(s)。
ps：注意 π(pi) 和 n，不是小写的n，别看错了

问：在制作电路板时，要求将这n条线分布到若干个绝缘层上，在同一层上的连线不能相交。电路布线问题要确定将哪些连线安排在第一层上，使得该层上有尽可能多的连线。

详细说明
首先 上下各有 n 个接线柱，用 a[i] 数组表示 与 上接线柱  相连线的 下接线柱，再用 set[i][j] 表示上接线柱 i 与下接线柱 j  相连线的 左边（包括 i ，j 连线）的最大不相交连线的个数。
ps（这里的 j ，i  和上面问题中说的不是一个东西，这里的 i指的是上接线柱，j指的是下接线柱）

1、公式如下：　　    

                如果   j  !=   a[i]    则   max(  set[i-1][j]，set[i][j-1]  )
set[i，j] =
                如果   j ==   a[i]   则   set[i-1][j-1] + 1   

       循环遍历   i 和  j  ，具体使用  i   X   j  的嵌套循环，其实就是每一个上接线柱和每一个下接线柱做一次匹配，这样就可以得出结果，set[n][n]即我们想要的结果。最后通过回溯把结果输出出来
               ==> j == a[i]，表示当上图中的某个上下接线柱相连时，这时这两个点不会在和其他的接线柱相连，
                                      这时在 （i ，j） 处的最大不相交连线的个数就应该是就是 第  i-1个上接线柱 和第 j-1个下接线柱时的 最大不相交连线的个数 + 1。这个+1很重要。
              ==>  j  != a[i]，表示当上图中的某个上下接线柱相连时，这时 i 点和 非 j 点相连， j 点和 非 i 点相连，
                                      这时在（ i ，j） 处的最大不相交连线的个数就应该和  ( i - 1，j ) 处最大不相交连线的个数、 ( i，j - 1)处最大不相交连线的个数中较大的最大不相交连线的个数相同。

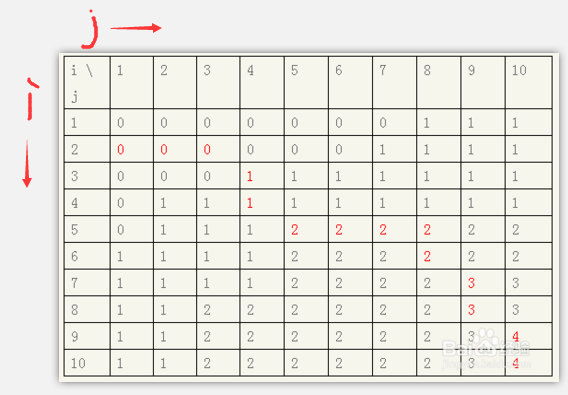
2、参考图如下：
       红色标明的就是算法选择的路径（向上优先，也可以用向左优先，答案都是四个，但值会有一点不同）。在斜角值改变时可以取得所求的子集。即 9->10,7->9, 5->5, 3->4

 

 

代码块

#include <stdio.h>
#include <stdlib.h>

#define MAX( a, b ) ( (a) > (b) ? (a) : (b) )
void circut( int a[], int set[][11], int n );
void back_track( int i, int j, int set[][11] );

int main()
{
    int    a[] = { 0, 8, 7, 4, 2, 5, 1, 9, 3, 10, 6 };
    int    set[11][11];

    circut( a, set, 10 );

    printf( "max set: %d 
", set[10][10] );
    back_track( 10, 10, set );
    printf( "
" );
    system( "pause" );
    return(0);
}

void circut( int a[], int set[][11], int n )
{
    int i, j;
    for ( i = 0; i < n; i++ )
    {
        set[i][0]    = 0;
        set[0][i]    = 0;
    }
    for ( i = 1; i <= n; i++ )
    {
        for ( j = 1; j <= n; j++ )
        {
            if ( a[i] != j )
                set[i][j] = MAX( set[i - 1][j], set[i][j - 1] );
            else
                set[i][j] = set[i - 1][j - 1] + 1;
        }
    }
}
void back_track( int i, int j, int set[][11] )
{
    if ( i == 0 )
        return;
    if ( set[i][j] == set[i - 1][j] )
        back_track( i - 1, j, set );
    else if ( set[i][j] == set[i][j - 1] )
        back_track( i, j - 1, set );
    else{
        back_track( i - 1, j - 1, set );
        printf( "(%d,%d) ", i, j );
    }
}

时间复杂度 
circut 的时间复杂度为O（n²）
back_track的时间复杂度为 O（n）
如有错误请指正。