1.定义树节点
二叉树是每个结点最多有两个子树的树结构,通常子树被称作“左子树”和“右子树”。
1 class Node(object): 2 """树的节点""" 3 def __init__(self, item): # 构建树节点时,需要传入节点数据元素 4 self.elem = item 5 self.lchild = None 6 self.rchild = None
2.初始化二叉树
1 class Tree(object): 2 """二叉树""" 3 def __init__(self): 4 self.root = None
3.二叉树基本操作
3.1.添加树节点
1 def add(self, item): # 尾插添加的方式 2 node = Node(item) # 构造节点 3 if self.root is None: 4 self.root = node 5 return 6 queue = [self.root] 7 while queue: # 寻找要添加的节点位置的循环控制条件 8 cur_node = queue.pop(0) # 取出队列头节点 9 if cur_node.lchild is None: # 当左节点为空时,在该左节点添加新节点 10 cur_node.lchild = node 11 return 12 else: 13 queue.append(cur_node.lchild) # 当左节点不为空时,把该左节点添加进待处理队列 14 if cur_node.rchild is None: # 当右节点为空时,在该右节点添加新节点 15 cur_node.rchild = node 16 return 17 else: 18 queue.append(cur_node.rchild)
3.2.层次遍历/广度遍历
1 def breadth_travel(self): 2 if self.root is None: # 空节点没有左右子节点,直接返回 3 return 4 queue = [self.root] 5 while queue: # 只要节点不为空,就应该继续遍历 6 cur_node = queue.pop(0) 7 print(cur_node.elem, end=" ") 8 if cur_node.lchild is not None: 9 queue.append(cur_node.lchild) 10 if cur_node.rchild is not None: 11 queue.append(cur_node.rchild)
3.3.深度遍历
3.3.1.递归形式
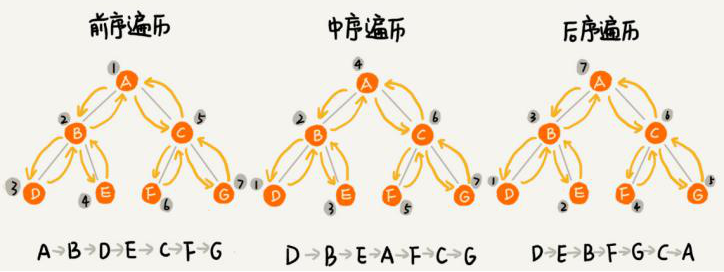
1 def rec_pre_travel(self, node): 2 """深度遍历/前序遍历:根-左-右""" 3 if node is None: # 递归终止条件 4 return 5 print(node.elem, end=" ") # 根 6 self.rec_pre_travel(node.lchild) # 左 7 self.rec_pre_travel(node.rchild) # 右 8 def rec_in_travel(self, node): 9 """深度遍历/中序遍历:左-根-右""" 10 if node is None: # 递归终止条件 11 return 12 self.rec_in_travel(node.lchild) # 左 13 print(node.elem, end=" ") # 根 14 self.rec_in_travel(node.rchild) # 右 15 def rec_post_travel(self, node): 16 """深度遍历/后序遍历:左-右-根""" 17 if node is None: # 递归终止条件 18 return 19 self.rec_post_travel(node.lchild) # 左 20 self.rec_post_travel(node.rchild) # 右 21 print(node.elem, end=" ") # 根
3.3.2.非递归形式
1 def non_rec_pre_travel(self): 2 """深度遍历/前序遍历:根-左-右""" 3 if self.root is None: # 递归终止条件 4 return 5 stack = [] # 使用栈模拟递归保存数据 6 temp_node = self.root # 当前要遍历的值 7 while temp_node or stack: # 使用栈和循环实现递归 8 while temp_node: # 节点入栈,直至遍历到叶子节点 9 print(temp_node.elem, end=" ") # 前序遍历打印节点的时机 10 stack.append(temp_node) 11 temp_node = temp_node.lchild # 继续遍历左节点 12 13 pop_node = stack.pop() 14 temp_node = pop_node.rchild # 下一个while循环的起点 15 def non_rec_in_travel(self): 16 """深度遍历/中序遍历:左-根-右""" 17 if self.root is None: # 递归终止条件 18 return 19 stack = [] # 使用栈模拟递归保存数据 20 temp_node = self.root # 当前要遍历的值 21 while temp_node or stack: # 使用栈和循环实现递归 22 while temp_node: # 节点入栈,直至遍历到叶子节点 23 stack.append(temp_node) 24 temp_node = temp_node.lchild # 继续遍历左节点 25 26 pop_node = stack.pop() 27 print(pop_node.elem, end=" ") # 中序遍历打印节点的时机 28 temp_node = pop_node.rchild # 下一个while循环的起点 29 def non_rec_post_travel(self): 30 """深度遍历/后序遍历:左-右-根""" 31 if self.root is None: # 递归终止条件 32 return 33 stack = [] # 使用栈模拟递归保存数据 34 temp_node = self.root # 当前要遍历的值 35 while temp_node or stack: # 使用栈和循环实现递归 36 while temp_node: # 节点入栈,直至遍历到叶子节点 37 stack.append(temp_node) 38 temp_node = temp_node.lchild # 继续遍历左节点 39 40 keep_node = stack[-1] # 先暂时不pop栈顶节点 41 temp_node = keep_node.rchild 42 if temp_node is None: # 如果keep_node的右节点为空,则可以打印keep_node了 43 keep_node = stack.pop() 44 print(keep_node.elem, end=" ") 45 # 判断pop出的keep_node是不是上一个节点的右节点 46 while stack and keep_node is stack[-1].rchild: 47 keep_node = stack.pop() # 如果是,表示上一个节点的右节点已经被pop,可以pop该节点了 48 print(keep_node.elem, end=" ")