题目：
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。
要求不能创建任何新的节点，只能调整树中节点指针的指向。我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。“head” 表示指向链表中有最小元素的节点。
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof
思路：
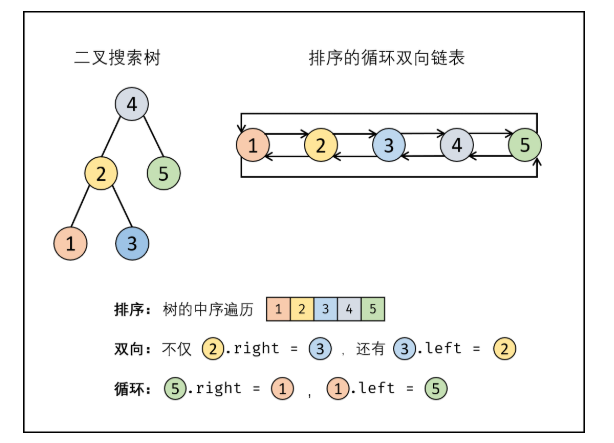二叉搜索树的中序遍历是递增序列，所以符合转换为排序链表的要求。
在构建相邻节点时，由于是双向链表(当前节点cur，前继节点pre)，所以不仅要求pre.right = cur，还要求cur.left = pre。
由于链表还是循环链表，因此需要连接首尾节点(head，tail)，得到head.left = tail， tail.right = head。
Python版本：
1 class Node: 2 def __init__(self, val, left=None, right=None): 3 self.val = val 4 self.left = left 5 self.right = right 6 7 class Solution: 8 def treeToDoublyList(self, root: 'Node') -> 'Node': 9 def dfs(cur): 10 if not cur: # 如果当前节点为空，说明已经越过叶节点，递归终止 11 return 12 13 dfs(cur.left) # 递归左子树 14 15 if self.pre: # 当前节点不是头结点，可以修改指针指向 16 self.pre.right = cur 17 cur.left = self.pre 18 else: # pre为空，说明当前是头节点，记录为head 19 self.head = cur 20 self.pre = cur # 将pre更新为cur 21 22 dfs(cur.right) # 递归右子树 23 if not root: return None 24 self.pre = None # pre位于cur左侧，初始化为None 25 dfs(root) 26 self.head.left = self.pre # 全部迭代完成后，pre指向双向链表中的尾节点 27 self.pre.right = self.head 28 return self.head
C++版本：
1 class Node { 2 public: 3 int val; 4 Node* left; 5 Node* right; 6 7 Node() {} 8 9 Node(int _val) { 10 val = _val; 11 left = NULL; 12 right = NULL; 13 } 14 15 Node(int _val, Node* _left, Node* _right) { 16 val = _val; 17 left = _left; 18 right = _right; 19 } 20 }; 21 22 class Solution { 23 public: 24 Node *pre; // 声明前继节点 25 Node *head; // 链表声明头结点 26 Node* treeToDoublyList(Node* root) { 27 if (root == NULL) return NULL; 28 pre = NULL; // pre位于链表头结点左侧，所以初始化前继节点为空 29 dfs(root); 30 head->left = pre; // 递归完成时，pre指向的是尾结点 31 pre->right = head; 32 return head; 33 } 34 35 void dfs(Node* cur) { 36 if (cur == NULL) 37 return; // 递归终止条件 38 39 dfs(cur->left); // 递归左子树 40 41 if (pre) { // pr非空说明cur不是头结点 42 pre->right = cur; 43 cur->left = pre; 44 } 45 else 46 head = cur; // 当前节点是头结点,记录为head 47 pre = cur; // pre更新为cur 48 49 dfs(cur->right); // 递归右子树 50 } 51 };