DS博客作业04--图

这个作业属于哪个班级	数据结构--网络2011/2012
这个作业的地址	DS博客作业04--图
这个作业的目标	学习图结构设计及相关算法
姓名	吴俊豪

0.PTA得分截图

1.本周学习总结

1.1 图的存储结构

随手画个图先

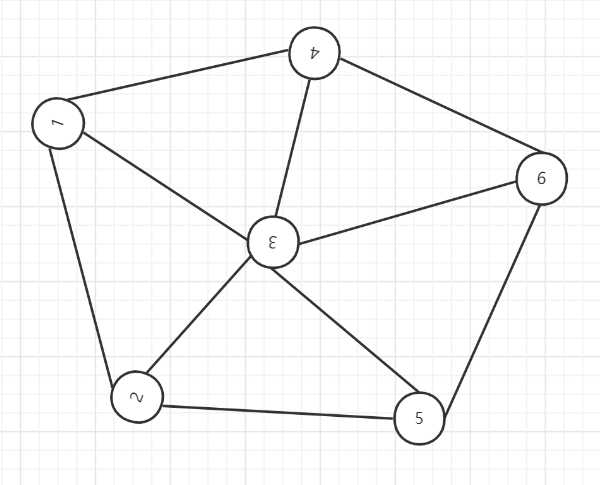
1.1.1 邻接矩阵

邻接矩阵的结构体定义

typedef struct              //图的定义
{  int edges[MAXV][MAXV];     //邻接矩阵
   int n,e;              //顶点数，边数
} MGraph;                //图的邻接矩阵表示类型

建图函数

void CreateMGraph(MGraph& g, int n, int e)//建图
{
    int i, j, a, b;
    for (i = 0; i < n; i++)//初始化邻接矩阵
    {
        for (j = 0; j < n; j++)
        {
            g.edges[i][j] = 0;
        }
    }

    for (i = 1; i <= e; i++)
    {
        cin >> a >> b;
        g.edges[a][b] = 1;
        g.edges[b][a] = 1;
    }
    g.n = n;
    g.e = e;
}

1.1.2 邻接表

邻接表的结构体定义

typedef struct ANode
{  int adjvex;            //该边的终点编号
   struct ANode *nextarc;    //指向下一条边的指针
   int info;    //该边的相关信息，如权重
} ArcNode;                //边表节点类型
typedef int Vertex;
typedef struct Vnode
{  Vertex data;            //顶点信息
   ArcNode *firstarc;        //指向第一条边
} VNode;                //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct 
{  AdjList adjlist;        //邻接表
   int n,e;        //图中顶点数n和边数e
} AdjGraph;   

建图函数

void CreateAdj(AdjGraph*& G, int n, int e) //创建图邻接表
{
    int i, j;
    int a, b;
    ArcNode* p;
    G = new AdjGraph;
    G->e = e;
    G->n = n;
    for (i = 0; i <= n; i++)
    {
        G->adjlist[i].firstarc = NULL;
    }
    for (i = 1; i <= e; i++)
    {
        cin >> a >> b;
        p = new ArcNode;
        p->adjvex = b;
        p->nextarc = G->adjlist[a].firstarc;
        G->adjlist[a].firstarc = p;

        p = new ArcNode;
        p->adjvex = a;
        p->nextarc = G->adjlist[b].firstarc;
        G->adjlist[b].firstarc = p;
    }
}

1.1.3 邻接矩阵和邻接表表示图的区别

一个我比较熟,一个不是很熟.
邻接矩阵:建立一个n*n的二维数组表示点与点之间的联系,其存在唯一,时间复杂度为O(n^2),对稠密图效果拔群(不过一般稀疏我也用).
领接表:建立n个链表来表示每一个结点和其他点之间的关系,存在不唯一,时间复杂度为O(n+e),对稀疏图效果略好.

1.2 图遍历

1.2.1 深度优先遍历

依然是这张图

遍历开始结点均为v=2;

邻接矩阵DFS

void DFS(MGraph g, int v)//深度遍历 
{
    MGraph* p;
    int i = 0;
    static int flag = 0;
    visited[v] = 1;
    if (!flag)
    {
        cout << v;
        flag = 1;
    }
    else
    {
        cout << " " << v;
    }
    for (i = 1; i <= g.n; i++)
    {
        if (g.edges[v][i]!=0&&visited[i]==0)
        {
            DFS(g, i);
        }
    }
}

结果如下:

2 1 3 4 6 5

邻接表DFS

void DFS(AdjGraph* G, int v)//v节点开始深度遍历 
{
    ArcNode *p;
    visited[v] = 1;
    static int flag = 1;
    if (flag)
    {
        cout << v;
        flag = 0;
    }
    else
    {
        cout  << " "<< v;
    }
    p = G->adjlist[v].firstarc;
    while (p)
    {
        if (!visited[p->adjvex])
        {
            DFS(G, p->adjvex);
        }
        p = p->nextarc;
    }
}

结果为:

2 5 6 4 3 1

1.2.2 广度优先遍历

邻接矩阵BFS

#include<queue>
void BFS(MGraph g, int v)//广度遍历 
{
    int t;
    queue<int>q;
    if (visited[v] == 0)
    {
        cout << v;
        visited[v] = 1;
        q.push(v);
    }
    while (!q.empty())
    {
        t = q.front();
        q.pop();
        for (int i = 1; i <= g.n; i++)
        {
            if (g.edges[t][i] == 1 && visited[i] == 0)
            {
                cout << " " << i;
                visited[i] = 1;
                q.push(i);
            }
        }
    }
}

结果:

2 1 3 5 4 6

邻接表BFS

void BFS(AdjGraph* G, int v)
{
    queue<int>q;
    q.push(v);
    ArcNode* p;
    int flag_2 = 1;
    int item;
    cout << v;
    visited[v] = 1;      //当前节点已访问过，数组值置为1
    while (!q.empty())
    {
        item = q.front();
        p = G->adjlist[item].firstarc;      //边指针ptr指向item表示的节点所连的第一条边
        while (p != NULL)
        {
            if (visited[p->adjvex] == 0)      //该边的终点还未被访问
            {
                q.push(p->adjvex);
                visited[p->adjvex] = 1;
                cout  << " "<< p->adjvex;
            }
            p = p->nextarc;
        }
        q.pop();
    }
}

结果:

2 5 3 1 6 4

可以看见,两种存储结构两种遍历结果有所差异,归其根本还是邻接表的表示方法不唯一.

1.3 最小生成树

所谓一个带权图的最小生成树，就是原图中边的权值最小的生成树，最小是指边的权值之和小于或者等于其它生成树的边的权值之和。

1.3.1 Prim算法求最小生成树

老图新用

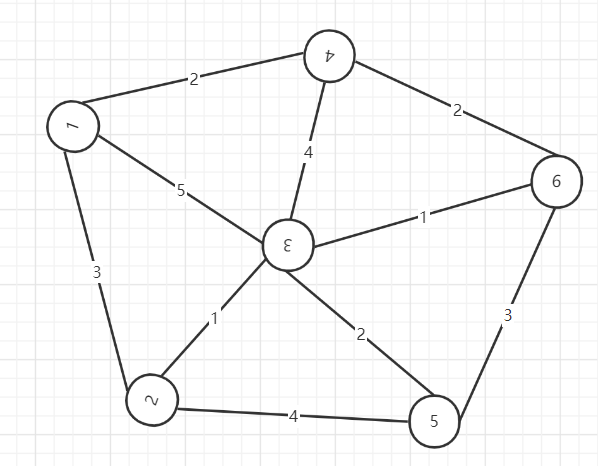
从节点v=1开始:

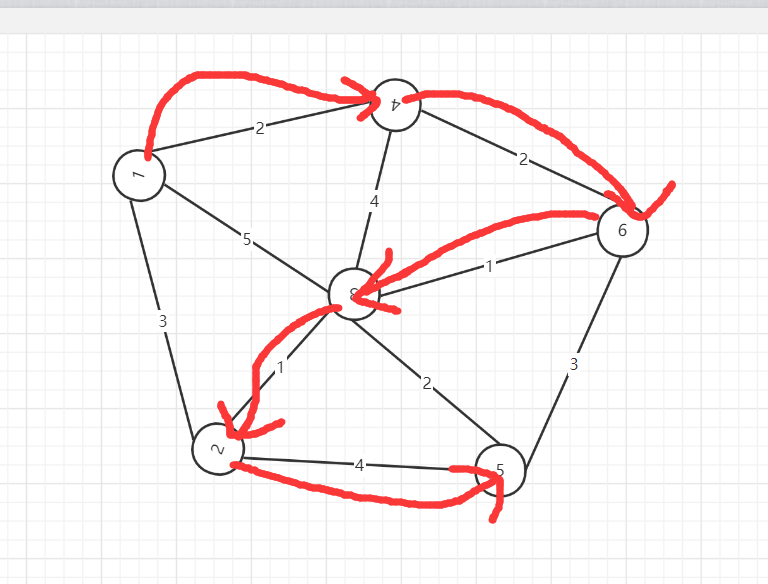
每次都寻找最小路径的下一个结点,被选中过的结点在visited数组里标记为1,直到找完n个结点.

实现Prim算法的2个辅助数组

visited[]:遍历时用到的数组,将经过的结点值置1.
lowcost[]:prim算法的核心数组, 用于比对并存放最小路径

Prim算法代码

int Prim(MGraph& g)//prim算法
{
    int lowcost[MAXV] = { 0 };
    int min, i, j, k;//最小 + 循环*2 + 防空
    int lenth = 0;
    lowcost[1] = 0;//从1村开始
    for (i = 2; i <= g.n; i++)
    {
        lowcost[i] = g.edges[1][i];
    }
    for (i = 2; i <= g.n; i++)//行数
    {
        min = 66235;
        j = 1;
        k = 0;
        while (j <= g.n)
        {
            if (lowcost[j] != 0 && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j;
            }
            j++;
        }
        if (k == 0)//有结点没遍历到
        {
            return -1;
        }
        lenth += min;
        lowcost[k] = 0;
        for (j = 2; j <= g.n; j++)
        {
            if (lowcost[j] != 0 && g.edges[k][j] < lowcost[j])
            {
                lowcost[j] = g.edges[k][j];//最小路径存入
            }
        }
    }
    return lenth;
}

分析Prim算法时间复杂度，适用什么图结构

Prim算法其时间复杂度为O(n^2)，与边得数目无关，适合稠密图.

1.3.2 Kruskal算法求解最小生成树

基于上述图结构求Kruskal算法生成的最小生成树的边序列

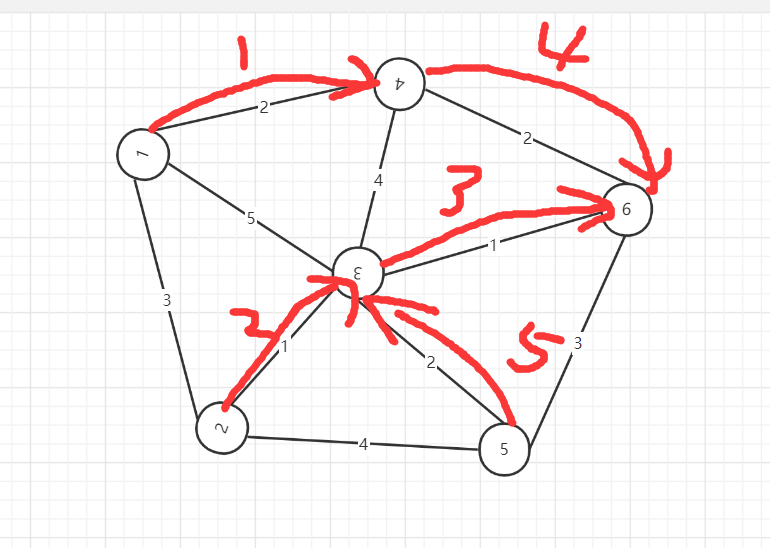
代码

int Kruskal(int n, int m){
    int nEdge = 0, res = 0;
    //将边按照权值从小到大排序
    qsort(a, n, sizeof(a[0]), cmp);
    for(int i = 0; i < n && nEdge != m - 1; i++){
        //判断当前这条边的两个端点是否属于同一棵树
        if(find(a[i].a) != find(a[i].b)){
            unite(a[i].a, a[i].b);
            res += a[i].price;
            nEdge++;
        }
    }
    //如果加入边的数量小于m - 1,则表明该无向图不连通,等价于不存在最小生成树
    if(nEdge < m-1) res = -1;
    return res;
}
int main(){
    int n, m, ans;
    while(scanf("%d%d", &n, &m), n){
        Init(m);
        for(int i = 0; i < n; i++){
            scanf("%d%d%d", &a[i].a, &a[i].b, &a[i].price);
            //将村庄编号变为0~m-1（这个仅仅只是个人习惯，并非必要的）
            a[i].a--;
            a[i].b--;
        }
        ans = Kruskal(n, m);
        if(ans == -1) printf("?
");
        else printf("%d
", ans);
    }
    return 0;
}

时间复杂度为O(e*log e),适用于邻接矩阵

1.4 最短路径

1.4.1 Dijkstra算法求解最短路径

void Dijkstra_sort(Graph G,int v0)
{
	int n=G.vexnum;
	int Path[n];//记录前驱
	int D[n]; //记录相对最短路径
	bool S[n];//判断当前路径长度是否为最短路径

	for(int i=0;i<n;i++)
	{
		S[i]=false;
		D[i]=G.arc[v0][i];
		if(D[i]<MaxInt)
		Path[i]=v0;
		else 
		Path[i]=-1;
	}
	S[v0]=true;
	D[v0]=0;
	//初始化
	int v;
	for(int i=0;i<n-1;i++)
	{
		int min=MaxInt;
		for(int w=0;w<n;w++)
		{

			if(D[w]<min&&!S[w])
			{
				min=D[w];
				v=w;
			}
			
		}
		S[v]=true;
		for(int w=0;w<n;w++)//修正贪心算法无法给出最优解的情况
		{
			if(!S[w]&&D[w]>(D[v]+G.arc[v][w]))
			{
				D[w]=D[v]+G.arc[v][w];
				Path[w]=v;
			}
		}
	}
	for(int i=0;i<G.vexnum;i++)
	{
		if(i!=v0)
		{
			cout<<v0<<"到"<<i<<"的最短路径="<<D[i]<<endl;
			cout<<"路线为: " ;
			for(int k=i;k!=v0;k=Path[k])
			{	
				cout<<k<<"<---";
			}
			cout<<v0<<endl;
		}
		
	}        
}

时间复杂度为O(n^2).

1.4.2 Floyd算法求解最短路径

Floyd算法解决给定的加权图中顶点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题

     #include 
     int main()  
      {  
     int e[10][10],k,i,j,n,m,t1,t2,t3;
       int inf=65535;
         scanf("%d %d",&n,&m);  
     for(i=1;i<=n;i++)  
     for(j=1;j<=n;j++)  
     if(i==j) e[i][j]=0;    
     else e[i][j]=inf;  
     //读入边
     for(i=1;i<=m;i++)  
         {  
             scanf("%d %d %d",&t1,&t2,&t3);  
             e[t1][t2]=t3;  
         }  
     //Floyd-Warshall算法核心语句
     for(k=1;k<=n;k++)  
     for(i=1;i<=n;i++)  
     for(j=1;j<=n;j++)  
     if(e[i][j]>e[i][k]+e[k][j] )   
                         e[i][j]=e[i][k]+e[k][j];  
     //输出最终的结果
     for(i=1;i<=n;i++)  
         {  
     for(j=1;j<=n;j++)  
             {  
                 printf("%10d",e[i][j]);  
             }  
             printf("
");  
         }  
     return 0;  
     }  

算法优势:能计算任意两个节点之间的最短路径

1.5 拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若<u，v> ∈E(G)，则u在线性序列中出现在v之前。

void toposort(int map[MAX][MAX],int indegree[MAX],int n)
{
    int i,j,k;
    for(i=0;i<n;i++) //遍历n次
    {
        for(j=0;j<n;j++) //找出入度为0的节点
        {
            if(indegree[j]==0)
            {
                indegree[j]--;
                cout<<j<<endl;
                for(k=0;k<n;k++) //删除与该节点关联的边
                {
                    if(map[j][k]==1)
                    {
                        indegree[k]--;
                    }
                }
                break;
            }
        }
    }
}

1.6 关键路径

AOE网

在一个表示工程的带权有向图中，用顶点表示事件（如V0），用有向边表示活动（如<v0,v1> = a1），边上的权值表示活动的持续时间，称这样的有向图为边表示的活动的网，简称AOE网

关键路径概念

具有最大路径长度的路径称为关键路径

关键活动

关键路径上的活动称为关键活动

2.PTA实验作业

2.1 六度空间

六度空间

2.1.1 解题思路

对每个结点使用广度优先搜索距离小于6的结点，并统计个数,再使用层数（level）来表示距离，其中起始结点为第0层
在广度遍历的过程中,先将起始节点入队,在队列不为空的情况下逐层遍历并实时记录层数level,当level=6时跳出循环

2.1.2 提交列表

2.1.3 知识点

图结构邻接矩阵的创建+图的广度遍历

2.2 村村通

公路村村通

2.2.1 解题思路

利用prim算法将自v村开始遍历每一个村庄并将最小路径存入lowcost[]中,将经过的村庄的visited[]置1,最后再遍历visited[]是否有村庄不通,若全通则将lowcost中的最短路径相加并输出

2.2.2 提交列表

2.2.3 知识点

邻接矩阵的创建+prim算法