前言(无关闲话):在此之前,课题小组讨论了三、四次,得有10个小时了总共,但都是很懵的样子,那就在这里深入地讲一下,顺便给自己理清一下思路。
认识虹吸
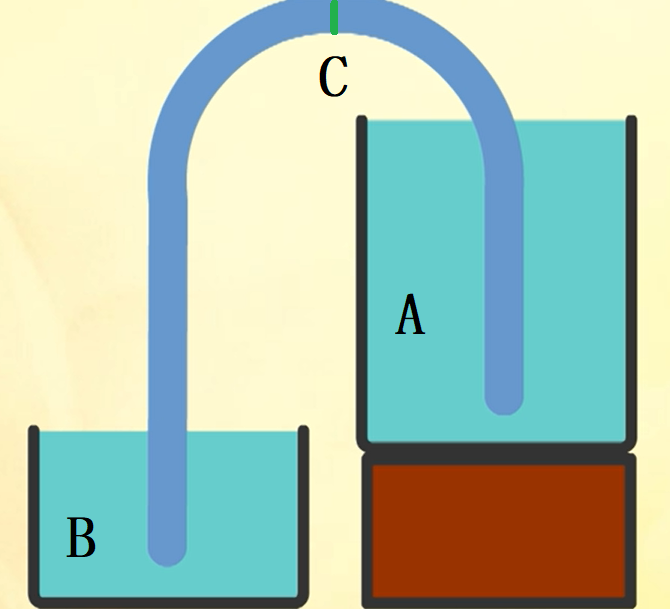
这就是虹吸的基本模型,再看一下百度的官方说法:
“虹吸(siphonage)是利用液面高度差的作用力现象,将液体充满一根倒U形的管状结构内后,将开口高的一端置于装满液体的容器中,容器内的液体会持续通过虹吸管向更低的位置流出。虹吸的实质是因为液体压强和大气压强而产生。”
通俗易懂地讲,即——两个高低不同的盛水器皿,用一个管子两头分别倒插,高位水会流向低位水。
OK,那么具体是怎样运作的呢?
Example 1
马桶就是一个很好的例子,这是它的内部构造图——
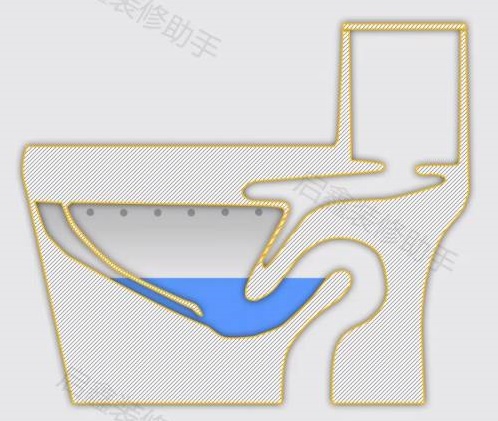
注意力放到吸水管部分(即流出部位)
为什么不弄成直的呢?弯的管子会不会更容易堵塞?
这是肯定的,但如果是直管,污水井、化粪池的臭味就会直接溢出来。
而之所以叫吸水管,也是因为在这个地方很好地利用了虹吸原理。
看不出?那我们先将模型套进来。

是不是一目了然了?
Example 2
背景:
明代洪武间,官府在景德镇开设御器厂,专门为皇宫制造御瓷。而传说当时的浮梁县令为了讨好皇帝,指令“御窑厂”的瓷工半年内制出一种“九龙杯”用来进贡皇上,瓷工们日夜研制,经过三个多月,几十次的反复试验,终于获得了成功。朱元璋得到“九龙杯”后,爱不释手,便经常使用这种珍品盛酒宴请文武大臣。
一次宴会上,朱元璋有意奖赏几位心腹大臣多喝一点酒,特意把酒添得满满的,而对平时喜欢直言不讳进谏忠言的大臣则将酒筛得很少。结果事与愿违,那几位被皇上有意照顾的大臣点酒未喝,御酒全部从“九龙杯”的底部漏光了,而其他大臣都高高兴兴地喝上了皇帝恩赐的御酒。皇帝对此甚是不解,究其原因,方知此杯盛酒最为公道,盛酒时只能浅平,不可过满,否则,杯中之酒便会全部漏掉,一滴不剩。
总结特性:知足者水存,贪心者水尽。
先看看这个杯子的奇葩外形:

再上此九龙杯(亦叫公道杯,下文同)结构图

可看到在公道杯中央有一龙头,体内有一空心瓷管,管下通杯底的小孔。
What's the use?
我们又可以看到图中将管子的最高处示意为“最高水面”。
但它并不是公道杯容量的最高水位,这是怎么回事?
结合背景,就说明倒得酒的多少便跟这“最高水面”,也就是这个管子有着很大的关系了
接下来,开始对模型分析一下吧!
虹吸现象的解剖
进入正题——
虹吸原理是液体压强和大气压强而产生。
So understanding the relationship between hydraulic pressure(液压) and atmospheric pressure(大气压) is the most important in this principle.
了解之前,你需要先知道液压计算公式:P=ρgh
(P为压强,单位为Pa(即帕斯卡);ρ为液体密度,单位一般为kg/m³;g为重力加速度,单位为9.8N/kg;h为液体深度/高度,单位一般为m)
由于液态分子间会存在引力与位能差能,液体会由压力大的一边流向压力小的一边。
而这里所说的压力,就包括了液压,和大气压。
在虹吸模型中,大气压是相差无几的,那么我们将其一律标为P₀。
而两盆水的重力加速度和密度显然都是一样的,就直接用g与ρ表示。
于是由公式可得这里存在的唯一变量(不考虑其他因素)就是h,分作h₁和h₂。
在图上做上标记:
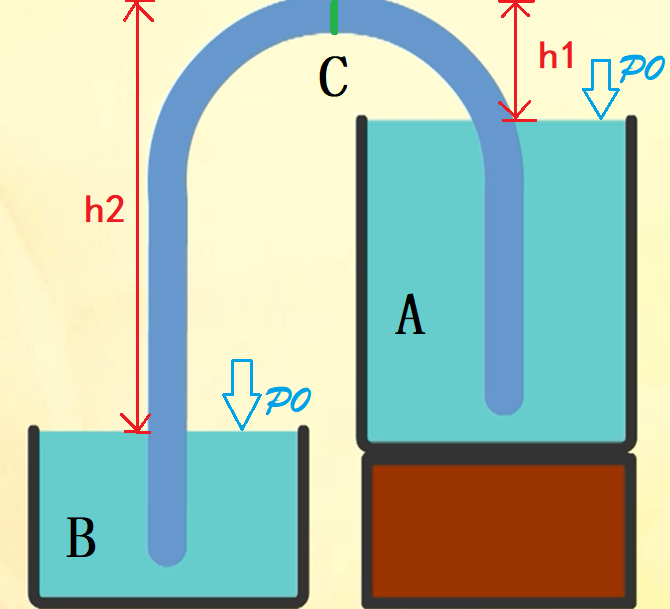
然后我们标高位水传达到最高处的压强为P₁,低位水为P₂。

那如何知道管内P1和P2的大小关系呢?
首先你要知道这些:
先找到两边与外界连通的静止液面,确定该面上的压强(即大气压P0)。
再以该液面为基准——
1)如果高于该液面(包括管内),压强等于该面压强减去ρgh;
2)如果低于该液面(包括管内),压强等于该面压强加上ρgh。
那么很明显,这里的h₁和h₂为最高面和两边液面的相对高度。
即可得出两个等式:
P₁=P₀-ρgh₁
P₂=P₀-ρgh₂
由于在算式中变量只有h,则易得P₁>p₂.
换个说法,就是高位给出的压强要大于低位给出的压强。
这也就很容易理解了,高位的水为什么会由于压强而流入低位了。
好了,水为什么会流的方面已经解决了,还有一个问题,这个水会不会停下来,如果会,又在什么时候停下来?
答案肯定是Yes的。
然后呢?
回想一下,之前是因为两边压强的不相等,水才会流动。
那么要让它停下来,肯定是要让压强相等,即p₁=p₂。
继续倒推,就是要使h₁=h₂,即管内最高处与液面相对高度相等。
所以当两边水面的最高处(液面)等高时,虹吸自然就会停下来了。
后传
说回公道杯。
这时候就会有小朋友(×)大佬(√)发问了:你说虹吸只要高低差大于0就好了,为什么这个杯子一定会流完,且一定要高于管内最高处才会开始流呢。
一个一个来说。
首先,在标准虹吸模型中确实如上面所说的会存在停下状况,但公道杯下面(管子低处)是没有水的,所以只要杯内有水,液面相对高度就一定大于0。
既然下面没有水,则低处的大气压不需要减去液压,故低处压强反而比高处压强要大了,所以此时的水连流都不可能。
所以这是我们的第二个问题,根据生活常识就可以知道,往杯内加入液体时,管内和管外的液面是保持一致且同时上升的。
而当液体高于管内最高处(不包含等于最高处)时,管内液体仍然处于增加状态,但已经没有了上升空间了。
没地方去,只能往下流,于是此时水就开始往另一边流了。
据本人的理解,此时的水往低处流的原因应该还不属于虹吸原理,只是单纯水的溢出而已。
而之后就不一样了。
当水不断流失,液面低于管内最高处时,由于水压以及重力的作用,水就会从最高水位持续向下流动。
此时低处有了液压,水压差已经开始出现,所以这个时候只能等所有水流完,虹吸才会停下了。
有疑问或发现错误欢迎提出。