动态规划
特点
- 计数型
- 有多少种方法选出k个数使得和是sum
- 求最大最小值
- 从左上角走到右下角路径的最大数字和
- 最长上升子序列长度
- 求存在性
- 取石子游戏,先手是否必胜
- 能不能选出k个数使得和是sum
解题步骤
- 确定状态
解动态规划的题,必然要创建一个数组,所谓状态,就是说数组每个元素f[i]或f[i][j]代表什么
两个重要分析条件
- 最后一步
- 子问题 - 转移方程
- 初始条件和边界情况
- 计算顺序
例题1
你有三种硬币,分别为2元,5元和7元,每种硬币都足够多;买一本书需要27元;如何用最少的硬币组合正好付清,不需要对方找钱
确定状态
最后一步&子问题
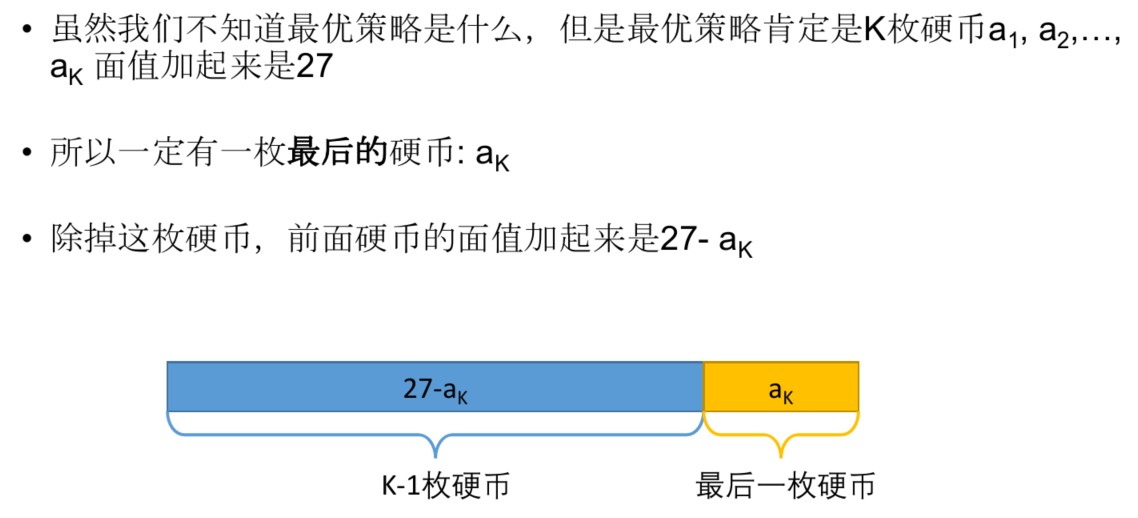

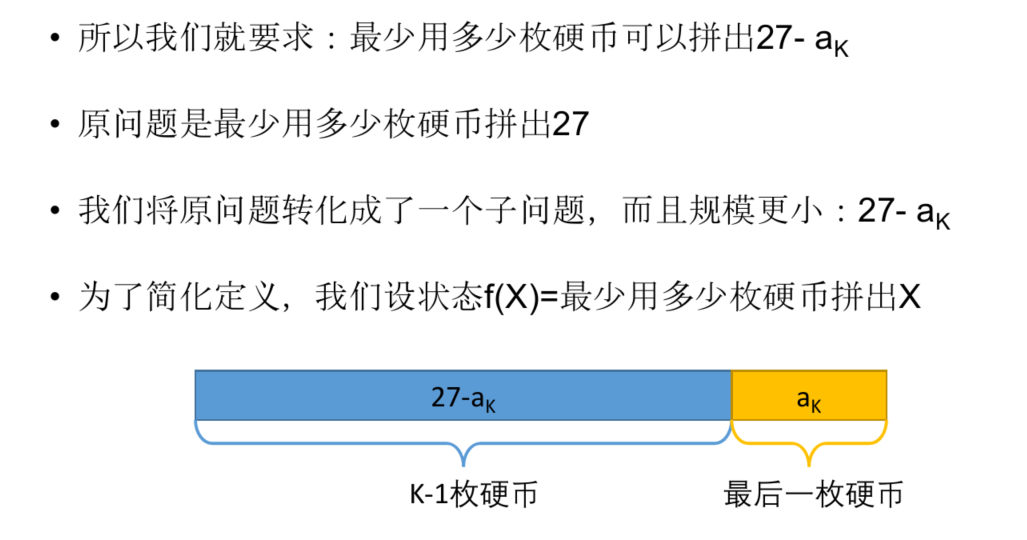


转移方程
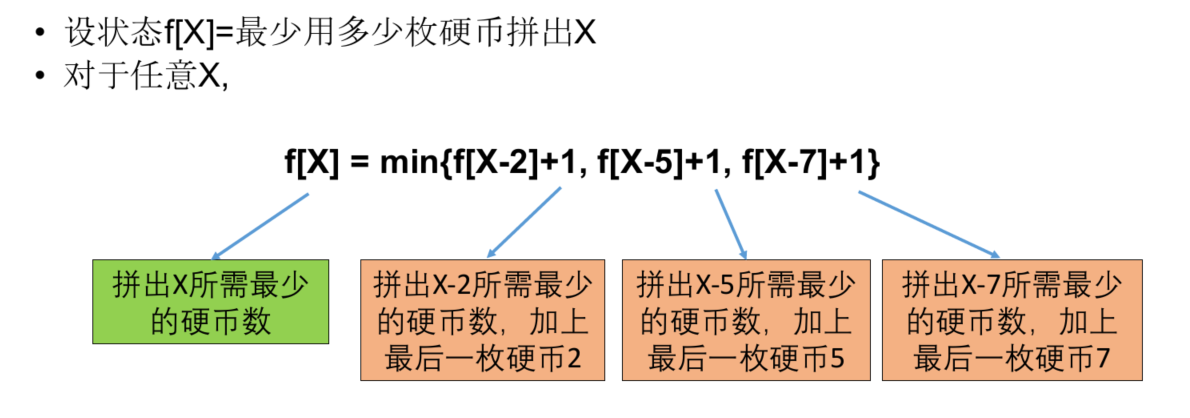
初始条件和边界情况

计算顺序

题解
public class Solution{
public int coinChange(in[] A,int M){
int n=A.length;
int[] f = new int[M+1];
f[0]=0;
int i,k;
for(i=1;i<=M;i++){
f[i]=Integer.MAX_VALUE;
for(k=0;k<n;k++){
if(i>=A[k]&&f[i-A[k]!=Integer.MAX_VALUE]){
f[i]=Math.min(f[i],f[i-A[k]]+i);
}
}
}
if(f[M] == Integer.MAX_VALUE)
return -1;
else
return f[M];
}
}
例题2 Unique Path
给定m行n列的网格,有一个机器人从左上角(0,0)出发,每一步可以向下或者向右走一步,问有多少种不同的方式走到右下角
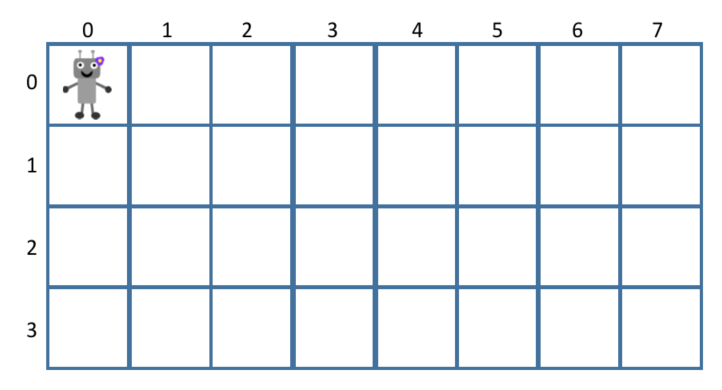
确定状态
最后一步
无论机器人用何种方式到达右下角,总有最后挪动的一步:向右或者向下,右下角坐标设为(m-1,n-1),那么前一步机器人一定是在(m-2,n-1)或者(m-1,n-2)
子问题
那么如果机器人有x种方式从左上角走到(m-2,n-1),有y种方式从左上角走到(m-1,n-2),则机器人有x+y种方式走到(m-1,n-1)
问题转化为
机器人有多少种方式从左上角走到(m-2,n-1)和(m-1,n-2)
而原题要求:有多少种方式从左上角走到(m-1,n-1)
状态
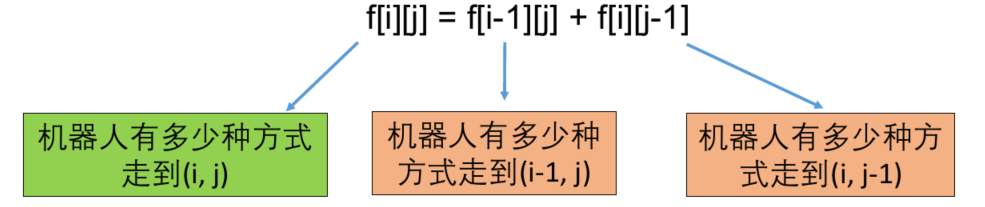
设f[i][j]为机器人有多少种方式从左上角走到(i,j)
转移方程
对任意一个格子(i,j)
f[i][j]=f[i-1][j]+f[i][j-1]
初始条件和边界情况
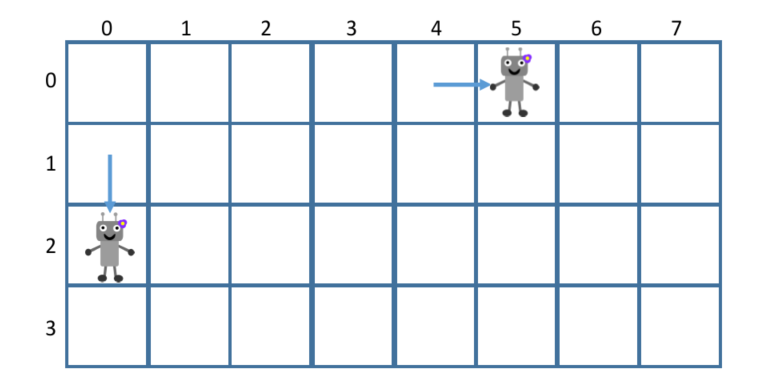
初始条件
f[0][0]=1,因为机器人只有一种方式到左上角(就算一步不走,也算一种走法)
边界情况
i=0或j=0,则前一步只能有一个方向过来(位于最下方,只能一直往右走;位于最右边,只能一直往下走;想象一下象棋里的兵)
计算顺序
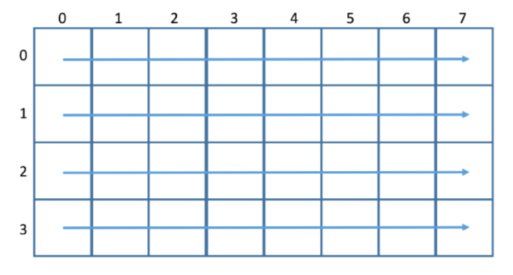
一行一行的算
一列一列的算其实也可以都一样
代码实现
public class UniquePath {
public int uniquePath(int m,int n){
//因为二维数组是从0开始的,最右下角是m-1和n-1,所以这里容量是m,n
int[][] f=new int[m][n];
int i,j;
for(i=0;i<m;i++){
for(j=0;j<n;j++){
//初始化
if(i==0||j==0){
f[i][j]=1;
continue;
}
//转移方程,可以看到,写出了转移方程,后面的都不难
f[i][j]=f[i-1][j]+f[i][j-1];
}
}
return f[m-1][n-1];
}
}
例题3
有n块石头分别在轴的0,1,...,n-1位置;一只青蛙在石头0,想跳到石头n-1;如果青蛙在第i块石头上,它最多可以向右跳距离$a_i$;问青蛙能否跳到石头n-1
确定状态
最后一步
如果青蛙能跳到最后一块石头n-1,我们考虑它跳的最后一步;这一步是从石头i跳过来,i<n-1;这需要两个条件同时满足
青蛙可以跳到石头i
最后一步不超过跳跃的最大距离:n-1-i<=$a_i$
子问题
青蛙能不能跳到石头i(i<n-1)
而我们原来的问题是求青蛙能不能跳到石头n-1
这就是我们的子问题
状态
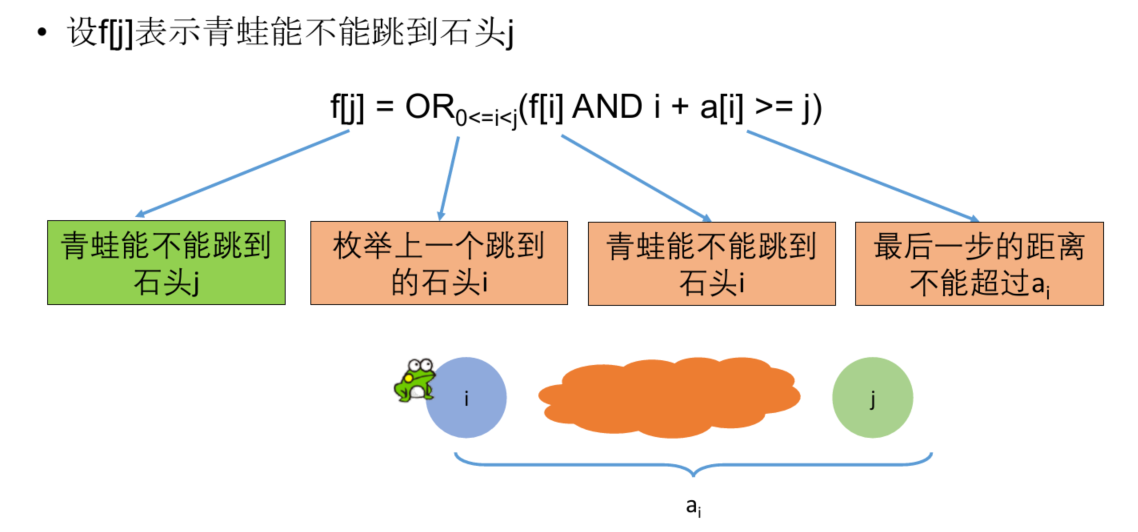
设f[j]表示青蛙能不能跳到石头j
转移方程
设f[j]表示青蛙能不能跳到石头j
初始条件和边界情况
f[0]=True
因为青蛙一开始就在石头0上
计算顺序
初始化f[0]=True
f[1],f[2],...,f[n-1]这个顺序
代码实现
public class JumpGame {
public boolean jump(int []A){
int n=A.length;//获取长度
boolean[] f=new boolean[n];
//初始化
f[0] =true;
int i,j;
for(j=1;j<n;j++){
f[j]=false;//初始化
for(i=0;i<j;i++){
if(f[i]&& i+A[i]>=j){
f[j]=true;
break;
}
}
}
return f[n-1];
}
}
例题4
给定a[0],...,a[n-1];找到最长的连续子序列i,i+1,i+2,...,j;使得a[i]*a[i+1]*...*a[j]最大
确定状态
最后一步
对于最优的策略(乘积最大),一定有最后一个元素a[j]
第一种情况:最优策略的序列就是{a[j]},答案是a[j]
第二种情况:连续子序列长度大于1,那么最优策略中a[j]前一个元素肯定是a[j-1]
如果a[j]是正数,我们希望以a[j-1]结尾的连续子序列乘积最大;如果a[j]是负数,我们希望以a[j-1]结尾的连续子序列乘积最小
所以要同时保存最大和最小两个极值
子问题
原问题可化为:求以a[j]结尾的连续子序列的最大乘积和以a[j]结尾的连续子序列的最小乘积;
两种情况都需要以a[j-1]结尾的乘积最大/小连续子序列
状态
设f[j]=以a[j]结尾的连续子序列的最大乘积,设g[j]=以a[j]结尾的连续子序列的最小乘积
转移方程
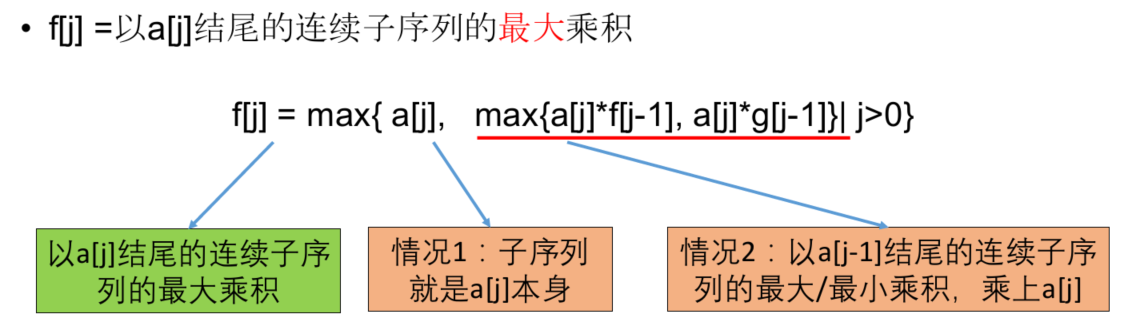
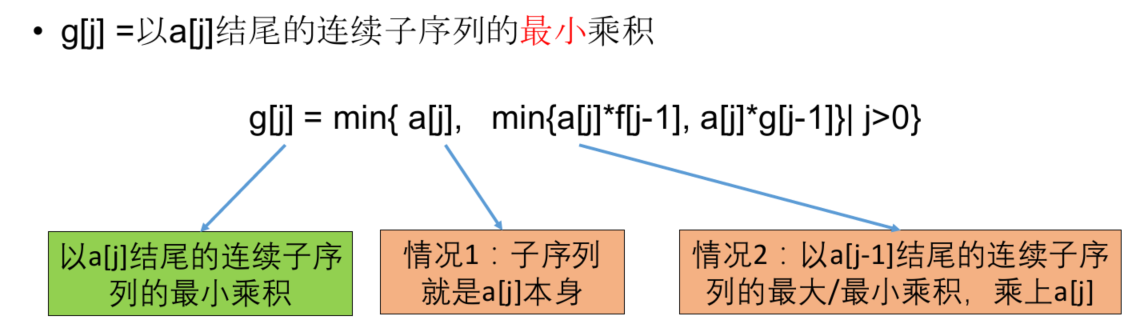
初始条件和边界情况
情况2必须满足:
j>0,即a[j]前面至少还有一个元素
初始条件:空
计算顺序
计算f[0]g[0]f[1]g[1]...f[n-1]g[n-1]
代码实现
public class MaxProduct {
public int maxProduct(int[] A){
int n=A.length;
if(n==0)
return 0;
int[] f =new int[n];
int[] g =new int[n];
int iccccccc;
//这一步还是有点疑问的,为什么要设一个MIN_VALUE呢?
//只不过是初始化而已,设个0都没问题
int res = Integer.MIN_VALUE;
for(i=0;i<n;i++){
//这一步不难理解,有一种情况是这个数就是序列本身
f[i]=A[i];
if(i>0){
f[i]=Math.max(f[i],Math.max(A[i]*f[i-1],A[i]*g[i-1]));
}
g[i]=A[i];
if(i>0){
g[i]=Math.min(f[i],Math.min(A[i]*f[i-1],A[i]*g[i-1]));
}
res = Math.max(res,f[i]);
}
return res;
}
}