1,
数据结构三要素:
1,逻辑结构:线性和非线性
2,存储结构:顺序,链式,索引,散列
3,数据运算:算法
具体时间复杂度与问题的规模和初始条件相关,分最佳和最大
2,
线性表:
无头结点:
头插法:s->data=ch;s->next=head;head=s;
尾插法:rear->next=s;rear=s; (两个指针头尾指针)
删除:q=p->next;p->next=q->next;free(q);
有头结点:有了头结点后,对在第一个元素结点前插入结点和删除第一个结点,其操作与对其它结点的操作统一了。
头插法:s->data=ch;s->next=head->next;head->next=s;
尾插法:rear->next=s;rear=s; (两个指针头尾指针)
删除:q=p->next;p->next=q->next;free(q);
循环链表:
单循环链表中设置尾指针比设置头指针更好
双循环链表:
前插:s->data=ch;s->prior=p->prior;s->next=p;p->prior->next=s;p->prior=s;
删除:p->prior->next=p->next;p->next->prior=p->prior;free(p);
链表逆序:
public static Node reversed_linkedlist() { MyLinkedList list = new MyLinkedList(); Node head = list.init(); if(head == null || head.next == null) { return head; } //使用三个节指针 Node current = head; Node newHead = null; Node next = null; while(current != null) { //先将当前节点的下个节点保存 next = current.next; current.next = newHead; //将原来的链表断链,将current的下一个结点指向新链表的头结点 newHead = current; //将current设为新表头 current = next; //将之前保存的next设为下一个节点 } return newHead; }
3,
栈:
顺序栈:(栈顶插入和删除,栈底为0)
- 初始栈:s->top=-1;
- 进栈:s->top++;S->data[s->top]=x;
- 出栈:x=S[s->top];s->top--;
链栈:链栈是没有附加头结点的运算受限的单链表。栈顶指针就是链表的头指针
- 进栈:p->data=x;p->next=S->top;S->top=p;(先进后出)S的next指向前面
- 出栈:S->top=p->next;free(p);
队列:
队头删除,队尾插入(银行排队)
顺序队列:
front和rear分别队头指针始终指向队头元素,尾指针始终指向队尾元素的下一位置
循环队列:为区分队列空和满:1,添加一个空;2,添加计数项
- 入队:Q->count++;Q->data[Q->rear]=x;Q->rear=(Q->rear+1)%QueueSize;
- 出队:Q->count--;Q->front=(Q->front+1)%QueueSize;
链式队列:
- 入队:p->data=x;Q->rear->next=p;Q->rear=p;
- 出队:p=Q->front;Q->front=p->next;free(p);
4,
树:
层次:根为第一层,最大层为树的高度,深度为根到该节点的路径长度;高度为叶节点到该节点最大路径
二叉树性质:
1,二叉树第i层上的结点数目最多为2i-1(i≥1)。
2,深度为k的二叉树至多有2^k-1个结点(k≥1)
3,在任意-棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则no=n2+1
4,具有n个结点的完全二叉树的深度为:log2[n](向下)+1或log2[n+1](向上)
二叉树存储形式:
1,顺序存储:第i个结点的孩子是2i,2i+1 (完全二叉树适用,如果该树不是完全二叉树,需要添加空节点构成完全二叉树)
2,二叉链表结构:左右指针,中间数据 |left|data|right|
二叉树遍历:
遍历是树进行其他运算的基础,前+中,中+后,层次+中(因为前后可以推出根结点,而中可以推左右) 使用递归思想来推树的结构能够快些
如:前+中
前:GDAFEMHZ 中:ADEFGHMZ
步骤:根据前知道root是G,根据中知道左子树是ADEF,右子树是HMZ
分析leftTree,由前知道root是D,so leftTree is:A,and rightTree is :EF
分析leftTree A ,结束,分析rightTree,From 前知道root 是F,From 中知leftTree is E
分析rigthTree HMZ,From 前知root is M,From 中知 leftTree is H,and rightTree is Z
遍历结束,树的层次遍历为 GDMAFHZE
如:中+后
中:ADEFGHMZ 后:AEFDHZMG
步骤:From 后,知道root 是G,From中知leftTree is ADEF,rightTree is HMZ;
分析leftTree:From 后知root is D,From 中leftTree is A ,rightTree is EF;
分析rightTree EF;From 后知:root is F,From 中leftTree is E;
分析rightTree HMZ;From 后知root is M ,From 中leftTree is H,rightTree is Z;
遍历结束,层次遍历为:GDMAFHZE
线索二叉树:左右标签为0,表示左右指针指向左右孩子节点,若为1,指向其左指向前驱,右指向后继(方便前,中,后遍历)
树转二叉树:二叉树左子树为树的子节点,右子树为兄弟,单个树即只有左侧,同样森林可以是左右子树的二叉树
同理二叉树转回森林和树:类似
树存储结构:
1,双亲链表表示法利用树中每个结点的双亲唯一性,在存储结点信息的同时,为每个结点附设一个指向其双亲的指针parent,惟一地表示任何-棵树。
2,孩子链表表示法是为树中每个结点设置一个孩子链表,并将这些结点及相应的孩子链表的头指针存放在一个向量中。类似hash
3,在存储结点信息的同时,附加两个分别指向该结点最左孩子和右邻兄弟的指针域leftmostchild和rightsibling,即可得树的孩子兄弟链表表示。
这种存储结构的最大优点是:它和二叉树的二叉链表表示完全一样
树(森林)的前序遍历:前序遍历一棵树(森林)恰好等价于前序遍历该树(森林)对应的二叉树
后序遍历树(森林)恰好等价于中序遍历该树(森林)对应的二叉树
树的路径:树的路径长度是从树根到树中每一结点的路径长度之和。在结点数目相同的二叉树中,完全二叉树的路径长度最短。
树的代价:结点的带权路径长度:结点到树根之间的路径长度与该结点上权的乘积
带权路径长度最小(即代价最小)的二叉树称为最优二叉树或哈夫曼树。
哈夫曼树:
1,n个叶子的哈夫曼树要经过n-1次合并,产生n-1个新结点。最终求得的哈夫曼树中共有2n-1个结点。
2,哈夫曼树是严格的二叉树,没有度数为1的分支结点。
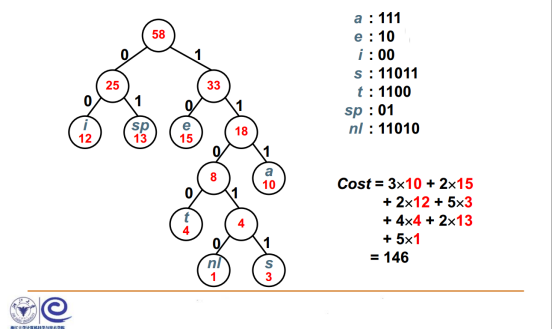
哈夫曼编码方式:
定长编码:如有6个字符,则n的位数定义为log26的上限为3位,定长为3位:000,001,010,011,100,101
变长编码:哈夫曼编码,根据树的深度,左子树为0,右子树为1:根:0,00,010等

用途:
编码:将每个字符编码成二进制位串
解码:将二进制位串转为字符
变长编码方案:变长编码方案将频度高的字符编码设置短,将频度低的字符编码设置较长
哈夫曼编码:压缩文件
1,构造哈夫曼树,确定每个单词所在的层次(n n=1,..),即哈夫曼二进制
2,计算代价:每个单词(叶节点)的层次(n-1)*单词出现的次数(权重值)之和为哈夫曼代价,实现压缩。
5,
图
图G的顶点数n和边数e的关系
若G是无向图,则0≤e≤n(n-1)/2
若G是有向图,则0≤e≤n(n-1)
无向图的度:无向图中顶点v的度(Degree)是关联于该顶点的边的数目,记为D(v),不分出度和入度
有向图的度:入度:以顶点v为终点的边的数目称为v的入度(Indegree);出度:以顶点v为始点的边的数目
图的边数等于度之和除以2
连通图:若V(G)中任意两个不同的顶点vi和vj都连通
有向边也称为弧(Arc),边的始点称为弧尾(Tail),终点称为弧头(Head)。
强连通图:有向图G中,若对于V(G)中任意两个不同的顶点vi和vj,都存在从vi到vj以及从vj到vi的路径,则称G是强连通图。
若将图的每条边都赋上一个权,则称这种带权图为网络
图邻接矩阵:时间复杂度O(n^2)
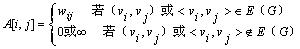
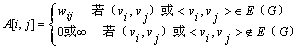
图邻接表:时间复杂度O(n+e)
表结点结构:邻接点域adjvex:存放与vi相邻接的顶点vj的序号j。链域next:将邻接表的所有表结点链在一起
头结点结构:顶点域vertex:存放顶点vi的信息;指针域firstedge:vi的邻接表的头指针
有向图分为:出边表和入边表

图遍历:
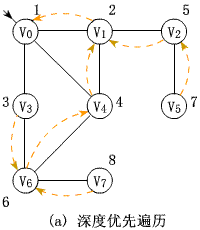
深度遍历:
使用栈,时间复杂度为O(n^2)(邻接矩阵)O(n+e)(邻接表)
上图的深度遍历: v0,v1,v2,v5,v4,v6,v3,v7
广度遍历:
使用队列:先进先出 时间复杂度为O(n^2)(邻接矩阵)O(n+e)(邻接表)
上图广度遍历是:V0,V1,V3,V4,V2,V6,V5,V7
生成树:
连通图G的一个子图是一棵包含G的所有顶点的树,则该子图称为G的生成树 (最小连通子图)
最小生成树:针对带权的网络,计算出整个网络通信所需要的最小成本
普利姆算法(prim):时间复杂度O(n^2),与图的边数无关,适合稠密图
流程初始顶点,选择其邻居中最小的边,更新邻居的边集,依次进行,直到所有顶点加入到生成树中

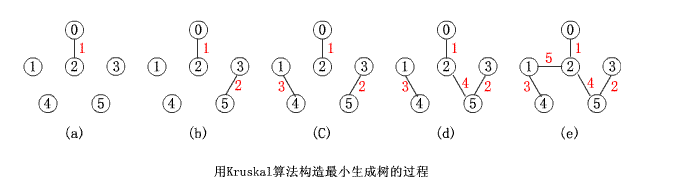
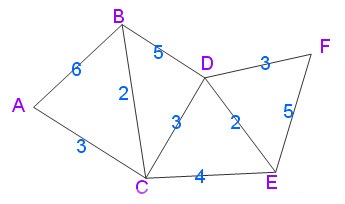
克鲁斯卡尔(Kruskal)算法:时间复杂度O(elge),适合稀疏图
流程:提取边的集合;找权值最小的边,寻找下一条边(如果该边使图变为环,舍去),直到全部顶点变为生成树时,结束
最短路径:
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。O(N^2) 不能计算权重为负,适合有向图计算如:

Floyd算法:是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3),空间复杂度为O(N2)。核心检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,流程具体如下:

2阶矩阵求法:从横竖交处为起始点a[0][0],选横线某点i为a[0][1]点,a[1][1]选i列不在斜线上的第j行的点, a[1][0]选取竖线上的第j行的点。判断方法:如果a[0][0]+a[0][1]+a[1][0]<a[1][1],则用相加值替代原先A[i][j]上的值。n行n列一次可以得到(n-1)*(n-2)各小矩阵,总共更新n次,获取到每个点之间的最短路径。


矩阵A3为最后结果每个点到其它点的最短路径,矩阵Path记录u,v两点之间最短路径所必须经过的点-------------------》参考博客和网站
最小生成树能够保证整个拓扑图的所有路径之和最小,但不能保证任意两点之间是最短路径。
最短路径是从一点出发,到达目的地的路径最小。(注意最小生成树prim和dijiksd算法不同)
拓扑排序:针对有向无环图,表示事件发生的先后顺序