数据结构之红黑树

Red-Black Tree | Set 1 (介绍)

 红黑树是一种平衡二叉树，其每个结点满足以下条件：

1. 每个结点都有颜色（黑或红）；
2. 根结点总是黑色；
3. 不存在两个相邻的红色结点（一个红色结点不能有红色的父结点或者红色子女结点）；
4. 从根到空节点的每条路径都有相同数量的黑色节点。

　　　

为什么选择红黑树？

　　大部分BST操作（e.g. 搜索，最大，最小，插入，删除…等）的时间复杂度为O（h），h为树的高度。对于一颗歪斜的BST而言，其时间复杂度可能会变成O(n) 。如果我们想确保每次插入和删除后树的高度总保持在Log（n），及时间复杂度为O（h），则我们需要采用红黑树。红黑树的高度总是保持在Log（n），n是树的结点数。

 红黑树 VS AVL 树

　　AVL树相对于红黑树而言更加的平衡，但在插入和删除过程中会涉及很多旋转操作。因此当你的应用需要频繁插入和删除的时候，红黑树或许是更好的选择；当你的应用不需要频繁的插入和删除，但需要频繁进行查询操作时，AVL树相比红黑树或许会更好。

红黑树是如何保持平衡的？

　　

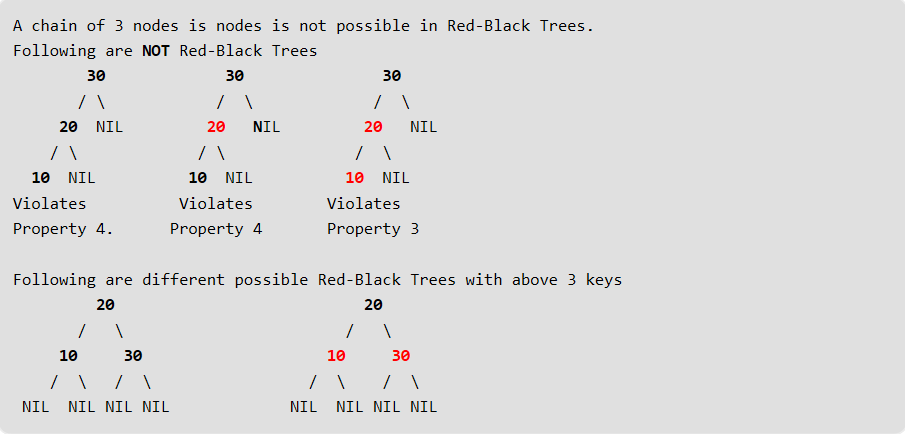
 红黑树的黑色高度       

　　黑色高度是从节点到叶子的路径上的黑节点数。叶节点也被计算为黑色节点。从上面的属性3和4，我们可以得出，高度h的节点有黑色高度> =h/2 。

每一个有n个节点的红黑树具有高度≤log2（n + 1）             

这可以用下面的事实来证明：             

　　1）对于一般的Binary Tree，令k为所有根到空结点路径上的最小节点数，n = 2^k-1（Ex. 如果 k为3，n为至少7）。这种表达也可以写为k≤log2（n + 1）             

　　2）从红黑树和上述4属性，我们可以说在红黑树有n个节点，根到叶的路径最多有log2（n + 1）个黑色结点。             

　　3）从红黑树的3属性，我们得出，在红黑树中黑色结点的数目至少为⌊n / 2⌋，n是节点总数。             

从以上3点，我们可以得出结论，事实上，有n个节点的红黑树具有高度h≤log2（n + 1）

Red-Black Tree | Set 2 (Insert)

　　对于AVL树而言，当进行插入操作后，我们通过旋转（Rotation）来实现树的再平衡。而在红黑树中，我们将通过以下两种操作来实现平衡：

　　1）Recoloring

　　2）Rotation

　　我们会尝试重新染色，当重新染色色不起作用时，则会进行旋转操作。

红黑树的插入

• 调用BST的插入算法，并为新元素结点染色；
• 若插入之前为空树，新结点作为根结点插入，染成黑色；
• 若插入前树非空，
  • 把新结点染成红色；
  • 若父结点是黑色，则算法结束；
  • 否则，进行 “双红调整” 。

　　

双红调整的情况

　　【叔父结点】指一个结点的父结点的兄弟结点

• 情况 1：叔父结点是红色：XYr
  • 需要换色
  • 换色后继续检查平衡！
• 情况 2：叔父结点是黑色：XYb
  • 需要旋转或重构
  • 每个结点的黑高度不变，调整完成

 　　

针对XYr的调整：换色

• 四种情况：LLr、RRr、LRr、RLr
• 以LLr为例：父祖换色

　　

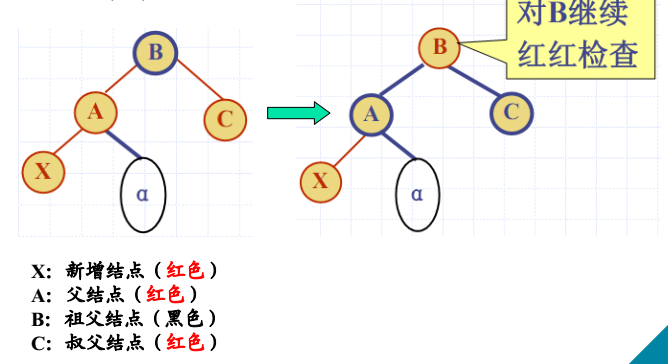
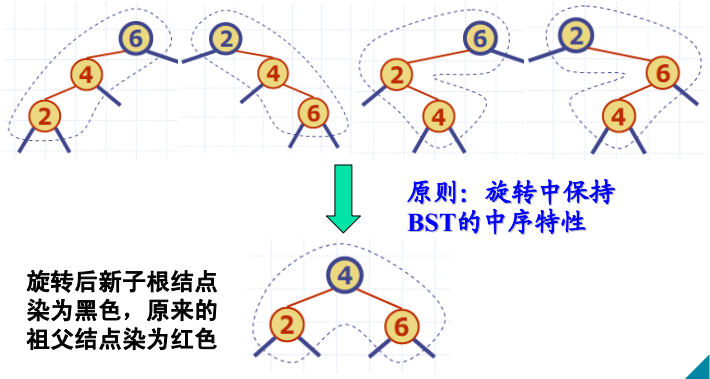
针对XYb的调整：旋转

• 四种情况：LLR、RRb、LRb、RLb

 　　

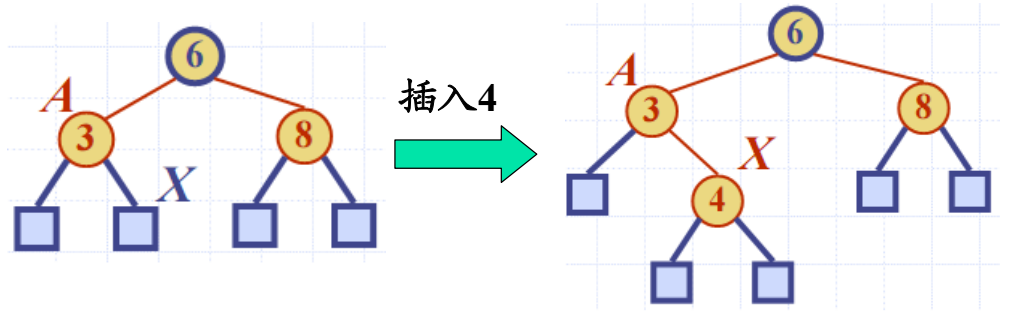
换色调整实例

• 插入4：首先调用BST的插入算法

　　

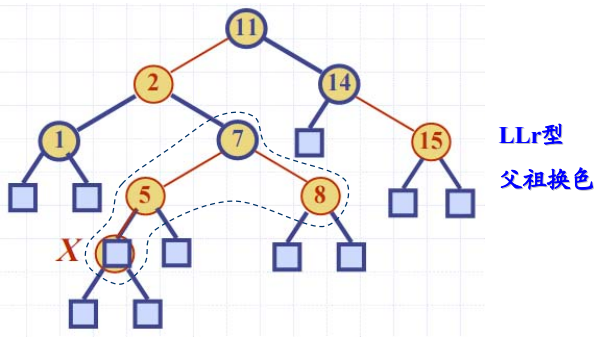
• 续 1

　　

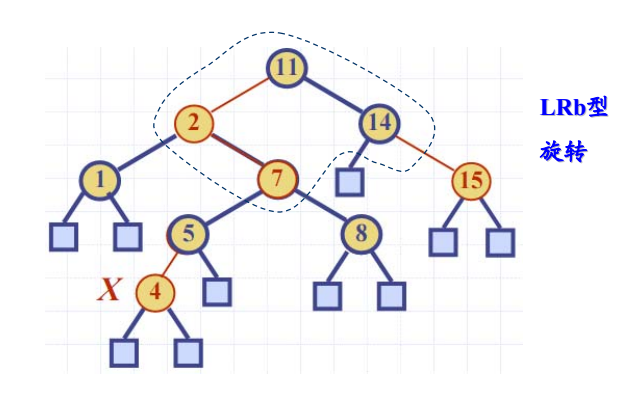
• 续 2

　　

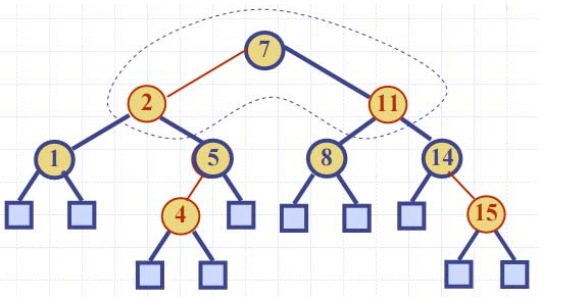
 Red-Black Tree | Set 2 (Delete)

红黑树结点的删除

• 先调用BST的删除算法
  • 如果被删除的结点有一个或两个外部结点，则直接删除；
  • 如果被删除的结点没有外部结点，则在右子树中寻找最小值结点（或在左子树中寻找最大结点），于该结点进行值交换（颜色不变）；
  • 此时最小值结点（或最大值结点）成为被删结点，转换为被删结点有一个或两个外部结点的情况。
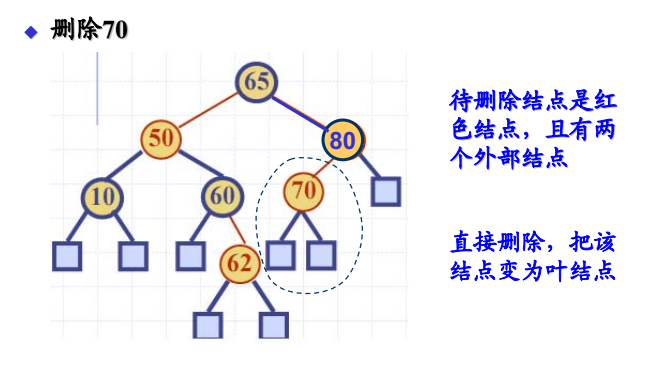
• 待删除结点有两个外部结点
  • 直接把该结点变为外部结点
  • 若该结点是红色，则算法结束
  • 若该结点是黑色，删除后红黑树不平衡！“双黑” 
• 待删除结点只有一个外部结点
  • 如果该结点是黑色，其非空子女结点为红色
  • 将其子女结点提升到该结点位置后，颜色变黑

 　　

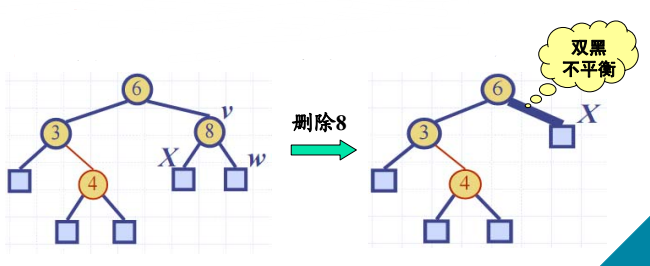
 双黑结点的调整

• 结点删除后，问题是：
  • 解决 “双黑” 结点现象
• 讨论前提：双黑结点是待删除结点的左子女结点（右子女结点对称处理即可）
• 有三种情况：
  • 双黑结点的兄弟结点是黑色，且兄弟结点的子女结点有红色
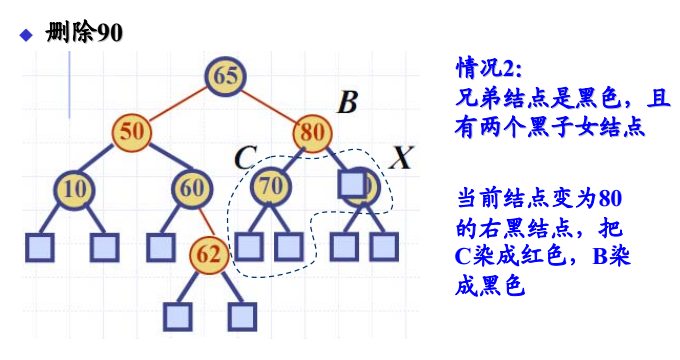
  • 双黑结点的兄弟结点是黑色，且兄弟结点有两个黑色子女结点
  • 双黑结点的兄弟结点是红色

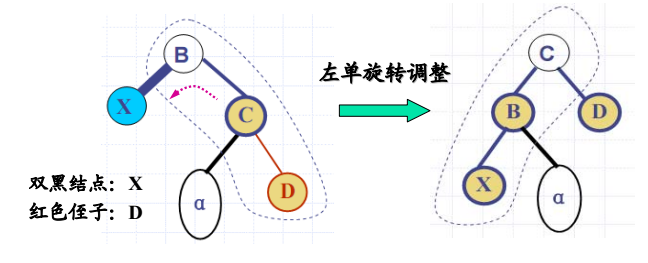
双黑结点调整：情况 1

• 双黑结点与其红色侄子 “八字形外撇”
• 解决方法：单旋转
  • 将兄弟结点C提上去
  • C继承原来父结点B的颜色
  • 把B染成黑色，D染黑色，其他颜色不变

　

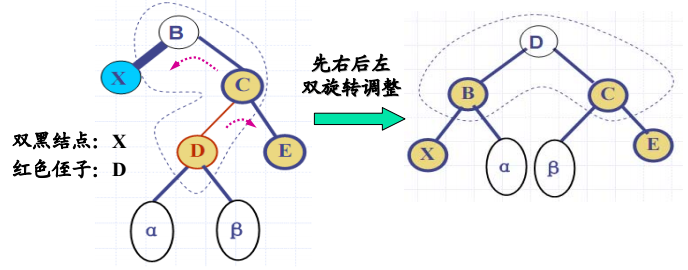
双黑结点调整：情况 1-2

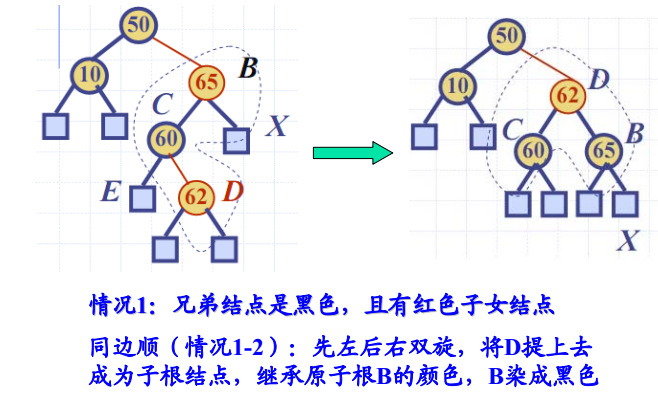
• 双黑结点与其红色侄子 “同边顺”
• 解决方法：双旋转　
  • 先右单旋，将D结点旋转为C结点的父结点
  • 再左d单旋，将D提上去作为根结点，继承原理子根B的颜色，B染成黑色

　　

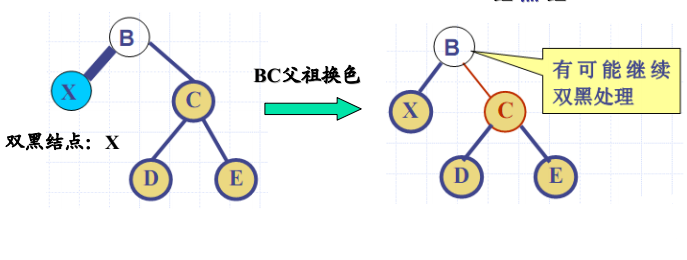
双黑结点调整：情况 2

• 双黑结点的兄弟结点是黑色，且有两个黑色子女结点
• 解决方法：父祖换色、继续检查
  • 把C染成红色，B染成黑色
  • 若B原为红色，则算法结束
  • 否则，对B继续作 “双黑” 调整

　　B原为红色：黑-红-黑  =》 黑-黑-红

　　B原为黑色：红-黑-黑  =》 红-黑-红

　　

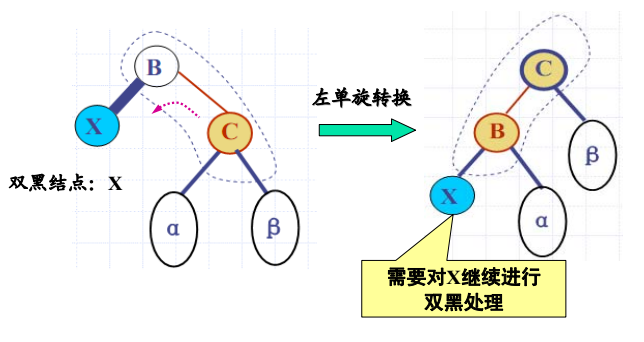
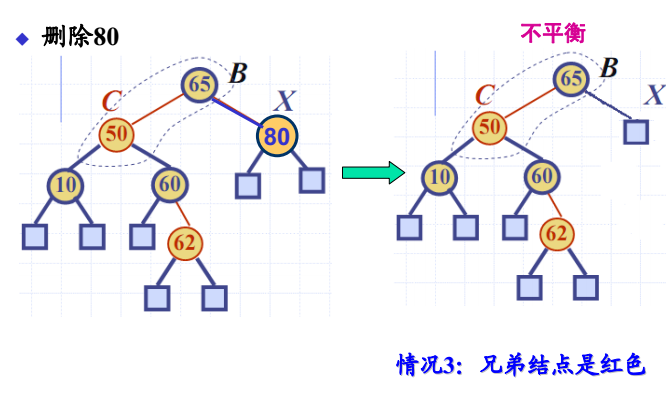
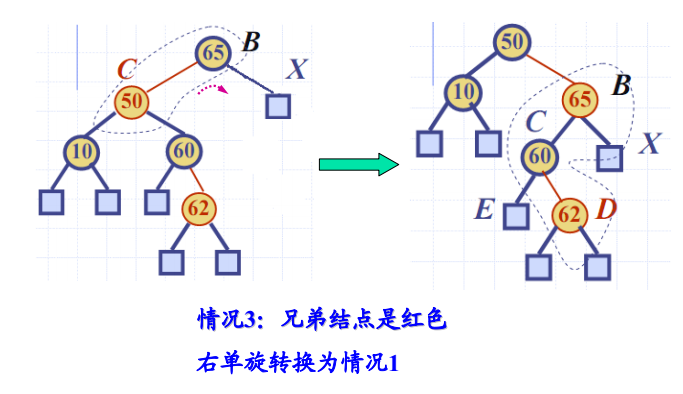
双黑结点调整：情况 3

• 双黑结点的兄弟结点是红色
• 解决方法：单旋转转换为情况1或情况2

　　

结点删除示例

　　

　　

　　

　

　　

红黑树插入、删除总结

• 　为了恢复红黑树的平衡，需要自底向根进行调整
• 红黑树的结点插入
  • 换色
  • 旋转或重构：双红调整
• 红黑树的结点删除
  • 重着色
  • 旋转或重构
  • 双黑结点调整
• 其平均和最差时间复杂度为 O(log2n)