x### 原题链接
https://www.luogu.com.cn/problem/P3622
题目大意
有一圈围栏,每个围栏有一种动物,有若干个小朋友,每个小朋友能看到连续的 (5) 个动物,每个小朋友对每种的动物的喜好不一样,如果一个小朋友会高兴,当且仅当 至少有一个他害怕的动物被移走,或者是至少有一个他喜欢的动物没有被移走。问调整某些动物后,最多有多少个小朋友会高兴。
分析
题目的目的是移走若干动物,使得所有的小朋友中,高兴的人数最多。其中问题的关键点在于如果确定了一个位置的小朋友所能看到的 (5) 个位置的动物的移动状态确定后,那么在他旁边的小朋友(如果存在)能看到的动物中有 (4) 个的状态也就是确定了,而且两者之间只有一位的状态可以选择,而且对应的只有移动和不移动两种状态。同时每种状态只有 (5) 位组成,因此可以考虑状压DP搞一下。
有个小细节需要注意,就是题目的图片中给出的小朋友位于他看到的 (5) 个位置的中间,而数据的输入格式给出的是他能看到的第一个位置编号x,因此我们可以统一一下,就认为能看到位置编号为 ({x,x+1,x+2,x+3,x+4}) 的小朋友位于 (x)。这样是不会影响答案的(因为小朋友所能看到的范围是不变的,只是站位不一样,当移动状态确定后,高兴的总人数是不变的)。
定义状态,设 (f[i][j]) 表示从 (1) 到 (i),位置 (i) 的小朋友能看到的动物的移动状态为 (j) 时,高兴人数的最大值,我们用 (1) 表示移动该动物,(0) 表示不移动。
考虑转移方程,先看下面的图片,其中 (x) 表示 (0) 或 (1):

当位置 (i) 的小朋友对应的动物移动状态为 (j) 时,那么与位置 (i-1) 的小朋友看到的动物移动状态 (j') 会有 (4) 位是重合的状态,因此 (j) 可以由上一个阶段的 (2) 个状态转移过来,分别对应的是 j&15<<1 和 j&15<<1|1,即取 (j) 的低四位作为 (j') 高四位,(j') 的最低位是 (0) 或 (1)。两者取 max 之后,还要加上位置 (i) 开始的连续 (5) 个位置的动物移动状态为 (j) 的时候,高兴的小朋友的人数。所以转移方程为:$$f[i][j]=max(f[i-1][(j&15)<<1],f[i-1][(j&15)<<1|1])+cnt[i][j]$$
这里注意运算符的优先级问题。
那么问题又来了,这个 (cnt[i][j]) 怎么求?
我们再重新强调一下它的定义:从 (i) 开始连续的 (5) 个动物的移动状态为 (j) 时,高兴的小朋友的人数。
根据我们前面的说的小细节的修改,输入中的 (E) 表示小朋友能看到的第一个位置,那么我们就认为这个小朋友站在 (E) 这个位置。后面给了我们他对某些动物的害怕和喜欢的情况,我们可以先组织一下他对这 (5) 个动物的害怕和喜欢的状态。假设他害怕的一个动物位于 (x),由于是环形,我们找一下 (x) 与 (E) 的相对位置:x = (x - E + n) % n,那么 fear |= (1 << x);like 也做同样的处理。根据题目中给出的是否高兴的条件,我们枚举每种移动的状态 (j):
- 至少有一个害怕的被移走:
(j & fear) != 0; - 至少有一个喜欢的没被移走:
(~j & like) != 0。
至此我们可以统计出cnt[i][j],大致代码如下:
// 记录每个小朋友害怕和喜欢的动物的状态
int fear = 0, like = 0;
for (int j = 0; j < f; ++j) {
qread(num); // 写的快读
num = (num - e + n) % n;
fear |= (1 << num);
}
// like也是一样的操作
// 处理起点e的区间移动状态对应的高兴的小朋友的数量
for (int j = 0; j < 32; ++j) { // 枚举每种移动状态
if ((fear & j) || (~j & like)) {
++cnt[e][j];
}
}
到这里我们基本可以补全代码了:
for (int i = 1; i <= lan; ++i) {
for (int j = 0; j < 32; ++j) {
f[i][j] = max(f[i-1][(j&15)<<1], f[i-1][(j&15)<<1|1]) + cnt[i][j];
}
}
然后找到 (f[n][...]) 当中的最大值?
提交上去会有红色的 WA
问题在于这是一个环,那么就必须要考虑到收尾相连的情况,也就是收尾重合的部分的动物移动状态也必须是相同的才行。
见下图:
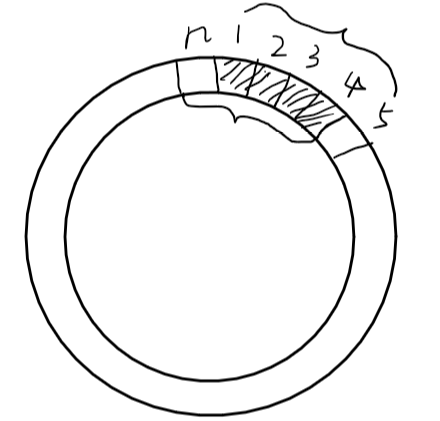
所有动物的移动状态确定后,我们必须保证选取的 (f[n][...]) 中的答案对应的状态 (j) 必须与 (1) 确定的状态中阴影部分是相同的,也就是说我们必须要保证最后的答案是从开始 (1) 阶段,对应的状态为阴影部分加上 (0) 或 (1) 而来。那要怎么保证呢?
我们可以枚举开始的状态,可以规定一个 (0) 阶段,枚举每个起始的状态 (s),初始化 (f[0][s]=0),其他值都初始化为绝对值大于总人数的负数(即负无穷),这样可以保证最终的答案必然会从我们的初始状态转移过来。那么针对这个起始状态 (s),我们的答案对应的是 (f[n][s]),只有这一个是可取的,只有这样才能保证我们的环形的客观条件。
补全代码:
int ans = 0;
for (int s = 0; s < 32; ++s) { // 枚举初始状态
memset(f[0], 128, sizeof(f[0])); // 足够小就可以,这里的足够小是对于题目中的人数来定的
f[0][s] = 0;
for (int i = 1; i <= lan; ++i) {
for (int j = 0; j < 32; ++j) {
f[i][j] = max(f[i-1][(j&15)<<1], f[i-1][(j&15)<<1|1]) + cnt[i][j];
}
}
ans = max(ans, f[lan][s]);
}