History repeat itself
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 460 Accepted Submission(s): 223
Problem Description
Tom took the Discrete Mathematics course in the 2011,but his bad attendance angered Professor Lee who is in charge of the course. Therefore, Professor Lee decided to let Tom face a hard probability problem, and announced that if he fail to slove the problem there would be no way for Tom to pass the final exam.
As a result , Tom passed.
History repeat itself. You, the bad boy, also angered the Professor Lee when September Ends. You have to faced the problem too.
The problem comes that You must find the N-th positive non-square number M and printed it. And that's for normal bad student, such as Tom. But the real bad student has to calculate the formula below.
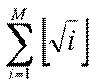
So, that you can really understand WHAT A BAD STUDENT YOU ARE!!
As a result , Tom passed.
History repeat itself. You, the bad boy, also angered the Professor Lee when September Ends. You have to faced the problem too.
The problem comes that You must find the N-th positive non-square number M and printed it. And that's for normal bad student, such as Tom. But the real bad student has to calculate the formula below.
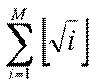
So, that you can really understand WHAT A BAD STUDENT YOU ARE!!
Input
There is a number (T)in the first line , tell you the number of test cases below. For the next T lines, there is just one number on the each line which tell you the N of the case.
To simplified the problem , The N will be within 231 and more then 0.
To simplified the problem , The N will be within 231 and more then 0.
Output
For each test case, print the N-th non square number and the result of the formula.
Sample Input
4 1 3 6 10
Sample Output
2 2 5 7 8 13 13 28
Source
Recommend
zhuyuanchen520
就是要求第a个非平方数是什么?
假设第a个非平方数是X,X前面有n个平方数,则n*n<X<(n+1)*(n+1);
n*n前面的非平方数的个数是n*n-n;
首先先根据a求n,n是满足不等式 n*n-n<a的最大正整数。
不等式的解是:
(1+sqrt(1+4*a))/2;必需对这个数上取整,然后减一就是n了。
然后第a个非平方数就是 n*n+(a-n*n+n)=a+n
之后就是求另一个式子的值了,首先求1~n*n-1求和:
(2*n-1)*(n-1)对它从2到n求和得到:n*(n+1)*(2*n+1)/3-3*n*(n-1)/2+n;
之后加上 (n+a-n*n+1)*n;
#include<stdio.h> #include<math.h> #include<algorithm> using namespace std; int main() { int T; scanf("%d",&T); long long a; while(T--) { scanf("%I64d",&a); double temp=ceil((1+sqrt(1+4*a))/2)-1; long long n=(long long)temp; long long res1=n+a; long long res2=n*(n+1)*(2*n+1)/3-3*(n+1)*n/2+n+(n+a-n*n+1)*n; printf("%I64d %I64d\n",res1,res2); } return 0; }
一开始以为要用高精度,就用JAVA写了个高精度的,也贴个代码吧:
import java.util.*; import java.math.*; import java.io.*; public class Main { public static void main(String[] args) { int T; Scanner cin=new Scanner(new BufferedInputStream(System.in)); T=cin.nextInt(); double a; for(int i=0;i<T;i++) { a=cin.nextDouble(); double n=Math.ceil((1+Math.sqrt(4*a+1))/2)-1; int res1=(int)(n+a); BigInteger res2=BigInteger.valueOf(0); BigInteger t1=BigInteger.valueOf(1); t1=t1.multiply(BigInteger.valueOf((int)n)); t1=t1.multiply(BigInteger.valueOf((int)(n+1))); t1=t1.multiply(BigInteger.valueOf((int)(2*n+1))); t1=t1.divide(BigInteger.valueOf(3)); BigInteger t2=BigInteger.valueOf(1); t2=t2.multiply(BigInteger.valueOf((int)n)); t2=t2.multiply(BigInteger.valueOf((int)(n+1))); t2=t2.multiply(BigInteger.valueOf(3)); t2=t2.divide(BigInteger.valueOf(2)); BigInteger t3=BigInteger.valueOf(0); t3=t3.add(BigInteger.valueOf((int)(n+a-n*n+1))); t3=t3.multiply(BigInteger.valueOf((int)n)); t3=t3.add(BigInteger.valueOf((int)n)); res2=res2.add(t1); res2=res2.subtract(t2); res2=res2.add(t3); //System.out.println(t1+" "+t2+" "+t3); System.out.println(res1+" "+res2); } } }