Eat the Trees
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1663 Accepted Submission(s): 783
Problem Description
Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
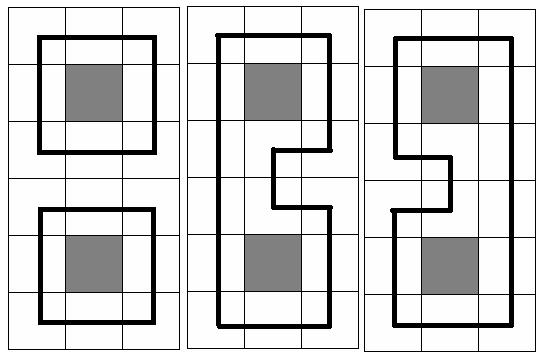
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))
So Pudge’s teammates give him a new assignment—Eat the Trees!
The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.
Now Pudge has a question, how many ways are there to eat the trees?
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.
Output
For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 263 – 1. Use the format in the sample.
Sample Input
2 6 3 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 2 4 1 1 1 1 1 1 1 1
Sample Output
Case 1: There are 3 ways to eat the trees. Case 2: There are 2 ways to eat the trees.
Source
Recommend
wangye
简单的多条回路插头DP。
三个代码。
第一个是模板风格。。。以后的都是这样了。
#include<stdio.h> #include<string.h> #include<iostream> #include<algorithm> using namespace std; const int HASH=10007; const int STATE=1000010;//状态数 const int MAXD=15; int N,M; int code[MAXD],maze[MAXD][MAXD]; struct HASHMAP { int head[HASH],next[STATE],state[STATE],size; long long f[STATE]; void init() { size=0; memset(head,-1,sizeof(head)); } void push(int st,long long ans) { int i,h=st%HASH; for(i=head[h];i!=-1;i=next[i]) if(st==state[i]) { f[i]+=ans; return; } f[size]=ans; state[size]=st; next[size]=head[h]; head[h]=size++; } }hm[2]; void decode(int *code,int m,int st) { int i; for(i=m;i>=0;i--) { code[i]=st&1; st>>=1; } } int encode(int *code,int m) { int i,st=0; for(int i=0;i<=m;i++) { st<<=1; st|=code[i]; } return st; } void init() { int i,j; scanf("%d%d",&N,&M); for(i=1;i<=N;i++) for(int j=1;j<=M;j++) scanf("%d",&maze[i][j]); for(int i=1;i<=N;i++)maze[i][M+1]=0;//边界补0 for(int i=1;i<=M;i++)maze[N+1][i]=0; } void shift(int *code,int m)//换行的时候移位 { int i; for(i=m;i>0;i--) code[i]=code[i-1]; code[0]=0; } void dpblank(int i,int j,int cur) { int k,left,up; for(k=0;k<hm[cur].size;k++) { decode(code,M,hm[cur].state[k]); left=code[j-1]; up=code[j]; if(left&&up)//11 -> 00 { code[j-1]=code[j]=0; if(j==M)shift(code,M); hm[cur^1].push(encode(code,M),hm[cur].f[k]); } else if(left||up)//01 或 10 { if(maze[i][j+1]) { code[j-1]=0; code[j]=1; hm[cur^1].push(encode(code,M),hm[cur].f[k]); } if(maze[i+1][j]) { code[j-1]=1; code[j]=0; if(j==M)shift(code,M);//这个不要忘了! hm[cur^1].push(encode(code,M),hm[cur].f[k]); } } else { if(maze[i][j+1]&&maze[i+1][j]) { code[j]=code[j-1]=1; hm[cur^1].push(encode(code,M),hm[cur].f[k]); } } } } void dpblock(int i,int j,int cur) { int k; for(k=0;k<hm[cur].size;k++) { decode(code,M,hm[cur].state[k]); code[j-1]=code[j]=0; if(j==M)shift(code,M); hm[cur^1].push(encode(code,M),hm[cur].f[k]); } } void solve() { int i,j,cur=0; long long ans=0; hm[cur].init(); hm[cur].push(0,1); for(i=1;i<=N;i++) for(j=1;j<=M;j++) { hm[cur^1].init(); if(maze[i][j])dpblank(i,j,cur); else dpblock(i,j,cur); cur^=1; } for(i=0;i<hm[cur].size;i++) ans+=hm[cur].f[i]; printf("There are %I64d ways to eat the trees.\n",ans); } int main() { //freopen("in.txt","r",stdin); //freopen("out.txt","w",stdout); int T; int iCase=0; scanf("%d",&T); while(T--) { iCase++; printf("Case %d: ",iCase); init(); solve(); } return 0; }
第二和第三是初学的时候写的。
 View Code
View Code
/* HDU 1693 */ #include<stdio.h> #include<string.h> #include<iostream> #include<algorithm> using namespace std; int mp[12][12]; long long dp[12][12][1<<12]; int main() { //freopen("in.txt","r",stdin); // freopen("out.txt","w",stdout); int T; int n,m; int iCase=0; scanf("%d",&T); while(T--) { iCase++; scanf("%d%d",&n,&m); for(int i=0;i<n;i++) for(int j=0;j<m;j++) scanf("%d",&mp[i][j]); memset(dp,0,sizeof(dp)); int cnt=1<<(m+1); dp[1][0][0]=1; for(int i=1;i<=n;i++) { for(int j=0;j<m;j++) { int t1=1<<j; int t2=1<<(j+1); for(int k=0;k<cnt;k++) { if(mp[i-1][j]) { if((k&t1)!=0&&(k&t2)!=0) dp[i][j+1][k-t1-t2]=dp[i][j][k]; else if((k&t1)==0&&(k&t2)==0) dp[i][j+1][k+t1+t2]=dp[i][j][k]; else { dp[i][j+1][k]+=dp[i][j][k]; dp[i][j+1][k^t1^t2]+=dp[i][j][k]; } } else { if((k&t1)==0&&(k&t2)==0) dp[i][j+1][k]=dp[i][j][k]; } } } if(i==n)continue; for(int j=0;j<(1<<m);j++) dp[i+1][0][j<<1]=dp[i][m][j]; } printf("Case %d: There are %I64d ways to eat the trees.\n",iCase,dp[n][m][0]); } return 0; }
 View Code
View Code
#include<stdio.h> #include<iostream> #include<string.h> #include<algorithm> using namespace std; long long dp[12][12][1<<12]; int mp[12][12]; int main() { // freopen("in.txt","r",stdin); // freopen("out.txt","w",stdout); int T; int n,m; int iCase=0; scanf("%d",&T); while(T--) { iCase++; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&mp[i][j]); memset(dp,0,sizeof(dp));//这个一定要加 dp[0][m][0]=1; for(int i=1;i<=n;i++) { for(int j=0;j<(1<<m);j++)//换行 dp[i][0][j<<1]=dp[i-1][m][j]; for(int j=1;j<=m;j++) for(int k=0;k<(1<<(m+1));k++) { int p=(1<<j); int q=(1<<(j-1)); if(mp[i][j]) { if((k&p)==0&&(k&q)==0)dp[i][j][k]=dp[i][j-1][k+p+q]; else if((k&p)!=0&&(k&q)!=0) dp[i][j][k]=dp[i][j-1][k-p-q]; else { dp[i][j][k]+=dp[i][j-1][k]; dp[i][j][k]+=dp[i][j-1][k^p^q]; } } else { if((k&p)==0&&(k&q)==0)dp[i][j][k]=dp[i][j-1][k]; } } } printf("Case %d: There are %I64d ways to eat the trees.\n",iCase,dp[n][m][0]); } }
