有关于范数的理解。
范数理解(0范数,1范数,2范数)
我们可以这样理解,一个集合(向量),通过一种映射关系(矩阵),得到另外一个集合(另外一个向量)。 **范数的本质是距离,存在的意义是实现比较。因为向量与矩阵无法像标量直接比较大小,因而通过范数(称为函数或者映射也可以)把不能比较的量转换为可以比较的实数。**
简单说:0范数表示向量中非零元素的个数(即为其稀疏度)。
1范数表示为,绝对值之和。
2范数则指模。
向量范数: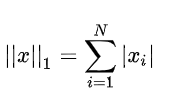
1-范数 ,即集合元素向量的绝对值之和。 2-范数,欧几里得范数,常用计算向量长度,即向量元素绝对值的平方和再开方,∞范数,即所有向量元素绝对值中的最大值。负无穷范数,即所有向量元素绝对值中的最小值。p范数,即向量元素绝对值的p次方和的1/p次幂。
矩阵范数: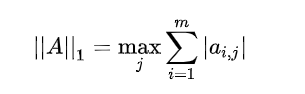
1-范数:列和范数,即所有矩阵列向量绝对值之和的最大值。
2-范数:谱范数,矩阵ATAA的最大特征值开平方根。
无穷范数:行和范数,即所有矩阵行向量绝对值之和的最大值。
F-范数:即矩阵元素绝对值的平方和再开平方
矩阵的核范数:矩阵的奇异值(将矩阵svd分解)之和。
矩阵的L0范数:矩阵的非0元素的个数,通常用它来表示稀疏,L0范数越小0元素越多,也就越稀疏.
矩阵的L1范数:矩阵中的每个元素绝对值之和,它是L0范数的最优凸近似,因此它也可以表示稀疏
矩阵的L2范数:就是F范数。
矩阵的L21范数:矩阵先以每一列为单位,求每一列的F范数(也可认为是向量的2范数),然后再将得到的结果求L1范数(也可认为是向量的1范数),很容易看出它是介于L1和L2之间的一种范数。