动态规划难吗?说实话,我觉得很难,特别是对于初学者来说,我当时入门动态规划的时候,是看 0-1 背包问题,当时真的是一脸懵逼。后来,我遇到动态规划的题,看的懂答案,但就是自己不会做,不知道怎么下手。就像做递归的题,看的懂答案,但下不了手,关于递归的,我之前也写过一篇套路的文章,如果对递归不大懂的,强烈建议看一看:为什么你学不会递归,告别递归,谈谈我的经验
对于动态规划,春招秋招时好多题都会用到动态规划,一气之下,再 leetcode 连续刷了几十道题
之后,豁然开朗 ,感觉动态规划也不是很难,今天,我就来跟大家讲一讲,我是怎么做动态规划的题的,以及从中学到的一些套路。相信你看完一定有所收获
如果你对动态规划感兴趣,或者你看的懂动态规划,但却不知道怎么下手,那么我建议你好好看以下,这篇文章的写法,和之前那篇讲递归的写法,是差不多一样的,将会举大量的例子。如果一次性看不完,建议收藏,同时别忘了素质三连。
为了兼顾初学者,我会从最简单的题讲起,后面会越来越难,最后面还会讲解,该如何优化。因为 80% 的动规都是可以进行优化的。不过我得说,如果你连动态规划是什么都没听过,可能这篇文章你也会压力山大。
一、动态规划的三大步骤
动态规划,无非就是利用历史记录,来避免我们的重复计算。而这些历史记录,我们得需要一些变量来保存,一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤,
如果你听不懂,也没关系,下面会有很多例题讲解,估计你就懂了。之所以不配合例题来讲这些步骤,也是为了怕你们脑袋乱了
第一步骤:定义数组元素的含义,上面说了,我们会用一个数组,来保存历史数组,假设用一维数组 dp[] 吧。这个时候有一个非常非常重要的点,就是规定你这个数组元素的含义,例如你的 dp[i] 是代表什么意思?
第二步骤:找出数组元素之间的关系式,我觉得动态规划,还是有一点类似于我们高中学习时的归纳法的,当我们要计算 dp[n] 时,是可以利用 dp[n-1],dp[n-2].....dp[1],来推出 dp[n] 的,也就是可以利用历史数据来推出新的元素值,所以我们要找出数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],这个就是他们的关系式了。而这一步,也是最难的一步,后面我会讲几种类型的题来说。
学过动态规划的可能都经常听到最优子结构,把大的问题拆分成小的问题,说时候,最开始的时候,我是对最优子结构一梦懵逼的。估计你们也听多了,所以这一次,我将换一种形式来讲,不再是各种子问题,各种最优子结构。所以大佬可别喷我再乱讲,因为我说了,这是我自己平时做题的套路。
第三步骤:找出初始值。学过数学归纳法的都知道,虽然我们知道了数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],我们可以通过 dp[n-1] 和 dp[n-2] 来计算 dp[n],但是,我们得知道初始值啊,例如一直推下去的话,会由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了,所以我们必须要能够直接获得 dp[2] 和 dp[1] 的值,而这,就是所谓的初始值。
由了初始值,并且有了数组元素之间的关系式,那么我们就可以得到 dp[n] 的值了,而 dp[n] 的含义是由你来定义的,你想求什么,就定义它是什么,这样,这道题也就解出来了。
不懂?没事,我们来看三四道例题,我讲严格按这个步骤来给大家讲解。
二、案例详解
案例一、简单的一维 DP
问题描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
(1)、定义数组元素的含义
按我上面的步骤说的,首先我们来定义 dp[i] 的含义,我们的问题是要求青蛙跳上 n 级的台阶总共由多少种跳法,那我们就定义 dp[i] 的含义为:跳上一个 i 级的台阶总共有 dp[i] 种跳法。这样,如果我们能够算出 dp[n],不就是我们要求的答案吗?所以第一步定义完成。
(2)、找出数组元素间的关系式
我们的目的是要求 dp[n],动态规划的题,如你们经常听说的那样,就是把一个规模比较大的问题分成几个规模比较小的问题,然后由小的问题推导出大的问题。也就是说,dp[n] 的规模为 n,比它规模小的是 n-1, n-2, n-3.... 也就是说,dp[n] 一定会和 dp[n-1], dp[n-2]....存在某种关系的。我们要找出他们的关系。
那么问题来了,怎么找?
这个怎么找,是最核心最难的一个,我们必须回到问题本身来了,来寻找他们的关系式,dp[n] 究竟会等于什么呢?
对于这道题,由于情况可以选择跳一级,也可以选择跳两级,所以青蛙到达第 n 级的台阶有两种方式
一种是从第 n-1 级跳上来
一种是从第 n-2 级跳上来
由于我们是要算所有可能的跳法的,所以有 dp[n] = dp[n-1] + dp[n-2]。
(3)、找出初始条件
当 n = 1 时,dp[1] = dp[0] + dp[-1],而我们是数组是不允许下标为负数的,所以对于 dp[1],我们必须要直接给出它的数值,相当于初始值,显然,dp[1] = 1。一样,dp[0] = 0.(因为 0 个台阶,那肯定是 0 种跳法了)。于是得出初始值:
dp[0] = 0.
dp[1] = 1.
即 n <= 1 时,dp[n] = n.
三个步骤都做出来了,那么我们就来写代码吧,代码会详细注释滴。
int f( int n ){
if(n <= 1)
return n;
// 先创建一个数组来保存历史数据
int[] dp = new int[n+1];
// 给出初始值
dp[0] = 0;
dp[1] = 1;
// 通过关系式来计算出 dp[n]
for(int i = 2; i <= n; i++){
dp[i] = dp[i-1] + dp[i-2];
}
// 把最终结果返回
return dp[n];
}
(4)、再说初始化
大家先想以下,你觉得,上面的代码有没有问题?
答是有问题的,还是错的,错在对初始值的寻找不够严谨,这也是我故意这样弄的,意在告诉你们,关于初始值的严谨性。例如对于上面的题,当 n = 2 时,dp[2] = dp[1] + dp[0] = 1。这显然是错误的,你可以模拟一下,应该是 dp[2] = 2。
也就是说,在寻找初始值的时候,一定要注意不要找漏了,dp[2] 也算是一个初始值,不能通过公式计算得出。有人可能会说,我想不到怎么办?这个很好办,多做几道题就可以了。
下面我再列举三道不同的例题,并且,再在未来的文章中,我也会持续按照这个步骤,给大家找几道有难度且类型不同的题。下面这几道例题,不会讲的特性详细哈。实际上 ,上面的一维数组是可以把空间优化成更小的,不过我们现在先不讲优化的事,下面的题也是,不讲优化版本。
案例二:二维数组的 DP
我做了几十道 DP 的算法题,可以说,80% 的题,都是要用二维数组的,所以下面的题主要以二维数组为主,当然有人可能会说,要用一维还是二维,我怎么知道?这个问题不大,接着往下看。
问题描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
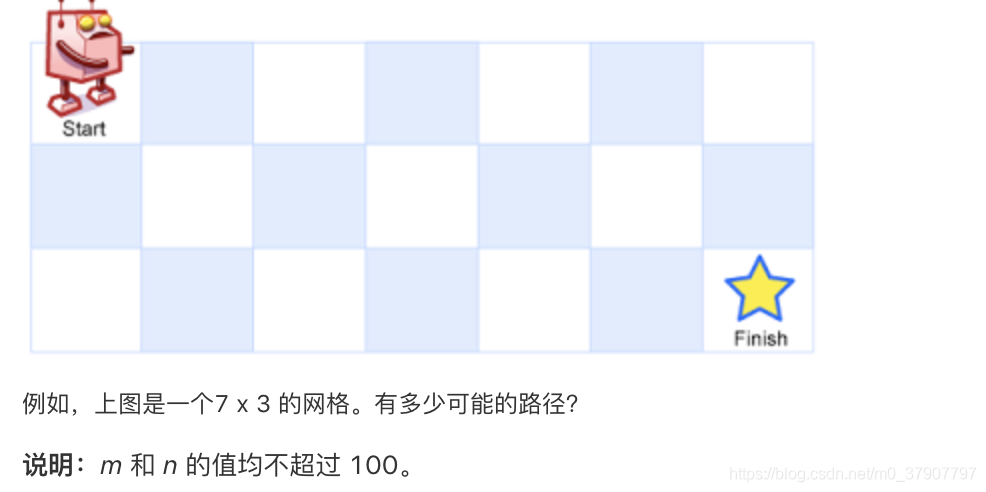
这是 leetcode 的 62 号题:https://leetcode-cn.com/problems/unique-paths/
还是老样子,三个步骤来解决。
步骤一、定义数组元素的含义
由于我们的目的是从左上角到右下角一共有多少种路径,那我们就定义 dp[i] [j]的含义为:当机器人从左上角走到(i, j) 这个位置时,一共有 dp[i] [j] 种路径。那么,dp[m-1] [n-1] 就是我们要的答案了。
注意,这个网格相当于一个二维数组,数组是从下标为 0 开始算起的,所以 右下角的位置是 (m-1, n - 1),所以 dp[m-1] [n-1] 就是我们要找的答案。
步骤二:找出关系数组元素间的关系式
想象以下,机器人要怎么样才能到达 (i, j) 这个位置?由于机器人可以向下走或者向右走,所以有两种方式到达
一种是从 (i-1, j) 这个位置走一步到达
一种是从(i, j - 1) 这个位置走一步到达
因为是计算所有可能的步骤,所以是把所有可能走的路径都加起来,所以关系式是 dp[i] [j] = dp[i-1] [j] + dp[i] [j-1]。
步骤三、找出初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的,相当于计算机图中的最上面一行和左边一列。因此初始值如下:
dp[0] [0….n-1] = 1; // 相当于最上面一行,机器人只能一直往右走
dp[0…m-1] [0] = 1; // 相当于最左面一列,机器人只能一直往下走
撸代码
三个步骤都写出来了,直接看代码
public static int uniquePaths(int m, int n) {
if (m <= 0 || n <= 0) {
return 0;
}
int[][] dp = new int[m][n]; //
// 初始化
for(int i = 0; i < m; i++){
dp[i][0] = 1;
}
for(int i = 0; i < n; i++){
dp[0][i] = 1;
}
// 推导出 dp[m-1][n-1]
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
O(n*m) 的空间复杂度可以优化成 O(min(n, m)) 的空间复杂度的,不过这里先不讲
案例三、二维数组 DP
写到这里,有点累了,,但还是得写下去,所以看的小伙伴,你们可得继续看呀。下面这道题也不难,比上面的难一丢丢,不过也是非常类似
问题描述
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
举例:
输入:
arr = [
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
和上面的差不多,不过是算最优路径和,这是 leetcode 的第64题:https://leetcode-cn.com/problems/minimum-path-sum/
还是老样子,可能有些人都看烦了,哈哈,但我还是要按照步骤来写,让那些不大懂的加深理解。有人可能觉得,这些题太简单了吧,别慌,小白先入门,这些属于 medium 级别的,后面在给几道 hard 级别的。
步骤一、定义数组元素的含义
由于我们的目的是从左上角到右下角,最小路径和是多少,那我们就定义 dp[i] [j]的含义为:当机器人从左上角走到(i, j) 这个位置时,最下的路径和是 dp[i] [j]。那么,dp[m-1] [n-1] 就是我们要的答案了。
注意,这个网格相当于一个二维数组,数组是从下标为 0 开始算起的,所以 由下角的位置是 (m-1, n - 1),所以 dp[m-1] [n-1] 就是我们要走的答案。
步骤二:找出关系数组元素间的关系式
想象以下,机器人要怎么样才能到达 (i, j) 这个位置?由于机器人可以向下走或者向右走,所以有两种方式到达
一种是从 (i-1, j) 这个位置走一步到达
一种是从(i, j - 1) 这个位置走一步到达
不过这次不是计算所有可能路径,而是计算哪一个路径和是最小的,那么我们要从这两种方式中,选择一种,使得dp[i] [j] 的值是最小的,显然有
dp[i] [j] = min(dp[i-1][j],dp[i][j-1]) + arr[i][j];// arr[i][j] 表示网格种的值
步骤三、找出初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的,相当于计算机图中的最上面一行和左边一列。因此初始值如下:
dp[0] [j] = arr[0] [j] + dp[0] [j-1]; // 相当于最上面一行,机器人只能一直往右走
dp[i] [0] = arr[i] [0] + dp[i] [0]; // 相当于最左面一列,机器人只能一直往下走
代码如下
public static int uniquePaths(int[][] arr) {
int m = arr.length;
int n = arr[0].length;
if (m <= 0 || n <= 0) {
return 0;
}
int[][] dp = new int[m][n]; //
// 初始化
dp[0][0] = arr[0][0];
// 初始化最左边的列
for(int i = 1; i < m; i++){
dp[i][0] = dp[i-1][0] + arr[i][0];
}
// 初始化最上边的行
for(int i = 1; i < n; i++){
dp[0][i] = dp[0][i-1] + arr[0][i];
}
// 推导出 dp[m-1][n-1]
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + arr[i][j];
}
}
return dp[m-1][n-1];
}
O(n*m) 的空间复杂度可以优化成 O(min(n, m)) 的空间复杂度的,不过这里先不讲
案例 4:编辑距离
这次给的这道题比上面的难一些,在 leetcdoe 的定位是 hard 级别。好像是 leetcode 的第 72 号题。
问题描述
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例:
输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
解答
还是老样子,按照上面三个步骤来,并且我这里可以告诉你,90% 的字符串问题都可以用动态规划解决,并且90%是采用二维数组。
步骤一、定义数组元素的含义
由于我们的目的求将 word1 转换成 word2 所使用的最少操作数 。那我们就定义 dp[i] [j]的含义为:当字符串 word1 的长度为 i,字符串 word2 的长度为 j 时,将 word1 转化为 word2 所使用的最少操作次数为 dp[i] [j]。
有时候,数组的含义并不容易找,所以还是那句话,我给你们一个套路,剩下的还得看你们去领悟。
步骤二:找出关系数组元素间的关系式
接下来我们就要找 dp[i] [j] 元素之间的关系了,比起其他题,这道题相对比较难找一点,但是,不管多难找,大部分情况下,dp[i] [j] 和 dp[i-1] [j]、dp[i] [j-1]、dp[i-1] [j-1] 肯定存在某种关系。因为我们的目标就是,**从规模小的,通过一些操作,推导出规模大的。对于这道题,我们可以对 word1 进行三种操作
插入一个字符
删除一个字符
替换一个字符
由于我们是要让操作的次数最小,所以我们要寻找最佳操作。那么有如下关系式:
一、如果我们 word1[i] 与 word2 [j] 相等,这个时候不需要进行任何操作,显然有 dp[i] [j] = dp[i-1] [j-1]。(别忘了 dp[i] [j] 的含义哈)。
二、如果我们 word1[i] 与 word2 [j] 不相等,这个时候我们就必须进行调整,而调整的操作有 3 种,我们要选择一种。三种操作对应的关系试如下(注意字符串与字符的区别):
(1)、如果把字符 word1[i] 替换成与 word2[j] 相等,则有 dp[i] [j] = dp[i-1] [j-1] + 1;
(2)、如果在字符串 word1末尾插入一个与 word2[j] 相等的字符,则有 dp[i] [j] = dp[i] [j-1] + 1;
(3)、如果把字符 word1[i] 删除,则有 dp[i] [j] = dp[i-1] [j] + 1;
那么我们应该选择一种操作,使得 dp[i] [j] 的值最小,显然有
dp[i] [j] = min(dp[i-1] [j-1],dp[i] [j-1],dp[[i-1] [j]]) + 1;
于是,我们的关系式就推出来了,
步骤三、找出初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n] 和所有的 dp[0….m] [0]。这个还是非常容易计算的,因为当有一个字符串的长度为 0 时,转化为另外一个字符串,那就只能一直进行插入或者删除操作了。
代码如下
public int minDistance(String word1, String word2) {
int n1 = word1.length();
int n2 = word2.length();
int[][] dp = new int[n1 + 1][n2 + 1];
// dp[0][0...n2]的初始值
for (int j = 1; j <= n2; j++)
dp[0][j] = dp[0][j - 1] + 1;
// dp[0...n1][0] 的初始值
for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1;
// 通过公式推出 dp[n1][n2]
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
// 如果 word1[i] 与 word2[j] 相等。第 i 个字符对应下标是 i-1
if (word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1];
}else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
}
}
}
return dp[n1][n2];
}
最后说下,如果你要练习,可以去 leetcode,选择动态规划专题,然后连续刷几十道,保证你以后再也不怕动态规划了。当然,遇到很难的,咱还是得挂。
Leetcode 动态规划直达:https://leetcode-cn.com/tag/dynamic-programming/
三、总结
上面的这些题,基本都是不怎么难的入门题,除了最后一道相对难一点,本来是要在写几道难一点,并且讲如何优化的,不过看了下字数,文章有点长了,关于如何优化的,后面再讲吧,在之后的文章中,我也会按照这个步骤,在给大家讲四五道动态规划 hard 级别的题,会放在每天推文的第二条给大家学习。如果大家感兴趣,文章看的人多,那么优化篇很快就会撸出来,不过感兴趣的人很少的话,动力比较少,可能就会慢一些,所以各位小伙伴,如果觉得有收获,不放三连走起来,嘻嘻。
另外,训练题也搞好了,嘻嘻
动归训练一:Leetcode 198.大家劫舍
还有递归的,最近也在更新
告别递归算法,谈谈我的一些经验