利用工具ECCTOOL解题
下载链接:https://bbs.pediy.com/thread-66683.htm

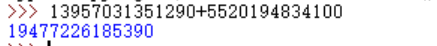
ECC相关原理
一般情况下,椭圆曲线可用下列方程式来表示,其中a,b,c,d为系数。
椭圆曲线基础理解:
E:y2=ax3+ bx2+cx+d加法
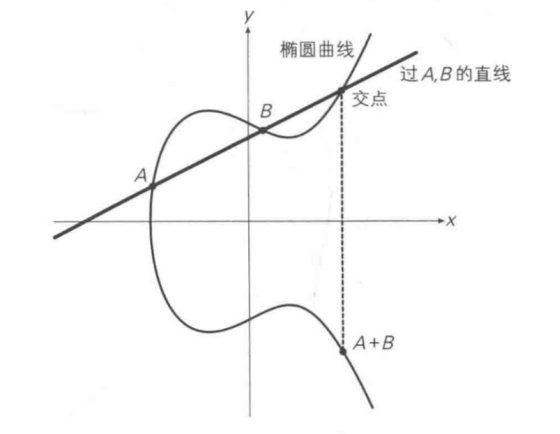
过曲线上的两点A、B画一条直线,找到直线与椭圆曲线的交点,交点关于x轴对称位置的点,定义为A+B,即为加法。如下图所示:A + B = C
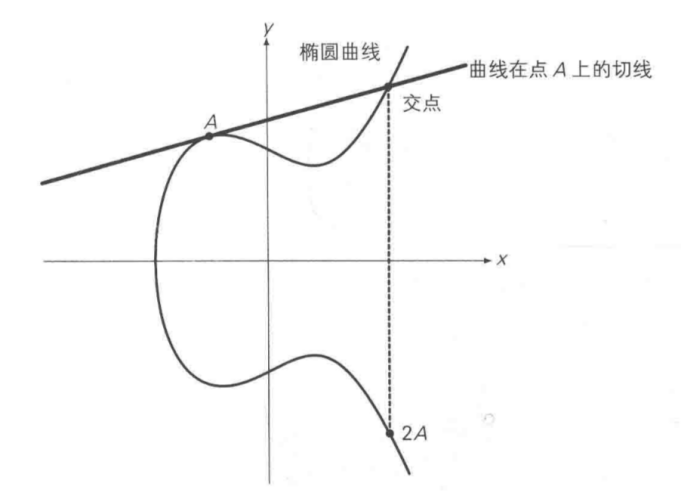
二倍运算
上述方法无法解释A + A,即两点重合的情况。因此在这种情况下,将椭圆曲线在A点的切线,与椭圆曲线的交点,交点关于x轴对称位置的点,定义为A + A,即2A,即为二倍运算。
椭圆曲线加密:
假设椭圆曲线为y² = x³ + x + 1,其在有限域GF(23)上时,写作: y² ≡ x³ + x + 1 (mod 23)
此时,椭圆曲线不再是一条光滑曲线,而是一些不连续的点,如下图所示。以点(1,7)为例,7² ≡ 1³ + 1 + 1 ≡ 3 (mod 23)。如此还有如下点:
(0,1) (0,22) (1,7) (1,16) (3,10) (3,13) (4,0) (5,4) (5,19) (6,4) (6,19) (7,11) (7,12) (9,7) (9,16) (11,3) (11,20) 等等。
另外,如果P(x,y)为椭圆曲线上的点,则-P即(x,-y)也为椭圆曲线上的点。如点P(0,1),-P=(0,-1)=(0,22)也为椭圆曲线上的点。
考虑K=kG ,其中K、G为椭圆曲线Ep(a,b)上的点,n为G的阶(nG=O∞ ),k为小于n的整数。则给定k和G,根据加法法则,计算K很容易但反过来,给定K和G,求k就非常困难。因为实际使用中的ECC原则上把p取得相当大,n也相当大,要把n个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据
点G称为基点(base point)
k(k<n)为私有密钥(privte key)
K为公开密钥(public key)
公钥加密:选择随机数r,将消息M生成密文C,该密文是一个点对,即:C = {rG, M+rK},其中K为公钥
私钥解密:M + rK - k(rG) = M + r(kG) - k(rG) = M 其中k、K分别为私钥、公钥。
