UVa 1354

There is a mysterious planet called Yaen, whose space is 2-dimensional. There are many beautiful stones on the planet, and the Yaen people love to collect them. They bring the stones back home and make nice mobile arts of them to decorate their 2-dimensional living rooms.

In their 2-dimensional world, a mobile is defined recursively as follows:

• a stone hung by a string, or
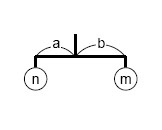
• a rod of length 1 with two sub-mobiles at both ends; the rod is hung by a string at the center of gravity of sub-mobiles. When the weights of the sub-mobiles are n and m , and their distances from the center of gravity are a and b respectively, the equation nxa = mxb holds.

For example, if you got three stones with weights 1, 1, and 2, here are some possible mobiles and their widths:

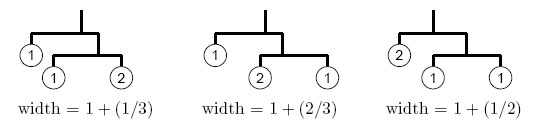
Given the weights of stones and the width of the room, your task is to design the widest possible mobile satisfying both of the following conditions.

• It uses all the stones.
• Its width is less than the width of the room.

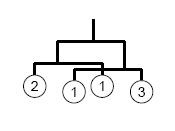
You should ignore the widths of stones. In some cases two sub-mobiles hung from both ends of a rod might overlap (see the figure on the right). Such mobiles are acceptable. The width of the example is (1/3) + 1 + (1/4) .

Input 

The first line of the input gives the number of datasets. Then the specified number of datasets follow. A dataset has the following format.

r

s

w₁

w_s

r is a decimal fraction representing the width of the room, which satisfies 0 < r < 10 . s is the number of the stones. You may assume 1s6 . w_i is the weight of the i -th stone, which is an integer. You may assume 1w_i1000 .

You can assume that no mobiles whose widths are between r - 0.00001 and r + 0.00001 can be made of given stones.

Output 

For each dataset in the input, one line containing a decimal fraction should be output. The decimal fraction should give the width of the widest possible mobile as defined above. An output line should not contain extra characters such as spaces.

In case there is no mobile which satisfies the requirement, answer `-1' instead.

The answer should not have an error greater than 0.00000001. You may output any numb er of digits after the decimal point, provided that the ab ove accuracy condition is satisfied.

Sample Input 

5 
1.3 
3 
1 
2 
1 
1.4 
3 
1 
2 
1 
2.0 
3 
1 
2 
1 
1.59 
4 
2 
1 
1 
3 
1.7143 
4 
1 
2 
3 
5

Sample Output 

-1 
1.3333333333333335 
1.6666666666666667 
1.5833333333333335 
1.7142857142857142

做这个题的时候一直调试不出正确结果，最后才发现是运算符+和&没有搞清楚，其实编译器已经给了一个警告，但是没引起注意，导致我调试了一个多小时！以后要注意看警告，ACM这种严谨的题目要尽量消除所有警告。

本题的用位运算来声称子集的方法值得学习。

#include <bits/stdc++.h>
using namespace std;

struct Node{
    double l, r;
    Node(double l, double r):l(l), r(r) {}
};
const int MAXN = (1<<6);
vector<Node> nodes[MAXN];
double r, w[6], sumw[MAXN];
int n, s;
bool vis[MAXN];

inline int bit_cnt(int x)
{
    return x == 0 ? 0 : bit_cnt(x / 2) + (x & 1);
}

void DFS(int n)
{
    if(vis[n]) return;
    vis[n] = true;
    if(bit_cnt(n)==1){
        nodes[n].push_back(Node(0, 0));
        return ;
    }
    for(int l = (n-1)&n; l > 0; l = (l-1)&n){
        int r = n^l;
        DFS(l), DFS(r);
        for(size_t i = 0; i < nodes[l].size(); i++)
            for(size_t j = 0; j < nodes[r].size(); j++){
                double ll = min(-sumw[r]/(sumw[l]+sumw[r]) + nodes[l][i].l, nodes[r][j].l + sumw[l]/(sumw[l]+sumw[r]));
                double rr = max(sumw[l]/(sumw[l]+sumw[r]) + nodes[r][j].r, nodes[l][i].r - sumw[r]/(sumw[l]+sumw[r]));
                nodes[n].push_back(Node(ll, rr));
            }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    int T; cin >> T;
    while(memset(sumw, 0, sizeof(sumw)), memset(vis, false, sizeof(vis)), T--){
        for(int i = 0; i < MAXN; i++)
            nodes[i].clear();
        cin >> r >> s;
        const int maxs = (1<<s)-1;
        for(int i = 0; i < s; i++)
            cin >> w[i];
        for(int i = 0; i <= maxs; i++)
            for(int j = 0; j < s; j++)
                if(i & (1<<j))
                    sumw[i] += w[j];
        DFS(maxs);
        double ans = -1.0;
        for(size_t i = 0; i < nodes[maxs].size(); i++)
            if(nodes[maxs][i].r - nodes[maxs][i].l < r)
                ans = max(ans, nodes[maxs][i].r - nodes[maxs][i].l);
        if(ans == -1) puts("-1");
        else printf("%.10f
", ans);
    }
    return 0;
}