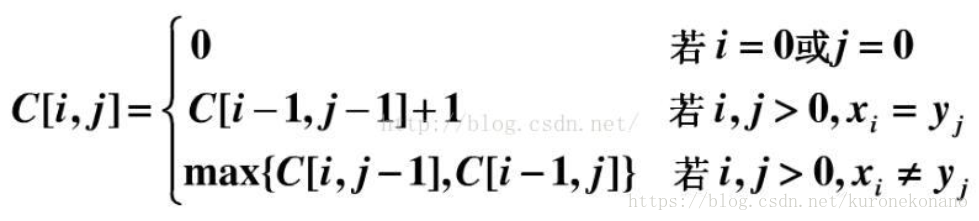链接:https://www.nowcoder.com/acm/contest/90/D
来源:牛客网
掌握未来命运的女神 psd 师兄在拿了朝田诗乃的 buff 后决定去实习。
埃森哲公司注册成立于爱尔兰,是一家全球领先的专业服务公司,为客户提供战略、咨询、数字、技术和运营服务及解决方案。他们立足商业与技术的前沿,业务涵盖40多个行业,以及企业日常运营部门的各个职能。凭借独特的业内经验与专业技能,以及翘楚全球的交付网络,他们帮助客户提升绩效,并为利益相关方持续创造价值。埃森哲是《财富》全球500强企业之一,目前拥有约41.1万名员工,服务于120多个国家的客户。于是psd打算去埃森哲公司投一下简历。
于是他用英文写了一篇简历,由于手速太快了以致自己都不知道写了什么。
然而面试官 xwc 一眼就看到了重点:大学打过 ACM!
xwc:“
听说你很低袄?考你个题:
忽略字母大小写,你这篇简历去掉最长的回文子序列后还有多长?
”
psd 顺手就把这个问题抛给了你。
输入描述:
多组输入,每组输入一个长度不超过 1234 的没空格的字符串,是 psd 的简历。
输出描述:
每组输出一个整数,如题。
示例1
输入
google
输出
2
示例2
输入
aBc,bAd
输出
2
所谓求最长回文子序列就是求原串和原串倒过来的LCS,注意题目中要求除去最长回文子序列剩下的长度。
那么如何求LCS呢。
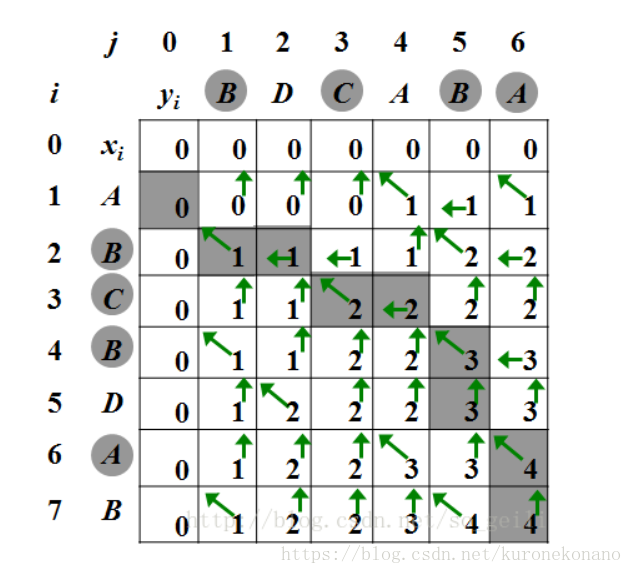
DP操作,DP数组中的i和j分别表示在两串中,分别取到前i位和前j位时,两个前缀子串所递推得到的最长公共子序列。
因此我们将数组中的0位【i,0】和【0,i】分别初始化为0,表示无论i是多少,另一个串前缀取几位,与当前串的空串都不会有任何公共子序列。
接着我们开始递推,遍历i,j以对比两串中相等的字符,一旦遇到相等的字符,我们将从i-1,j-1的位置继承状态,并延续继承到的最长公共子序列的记录值,也就是+1操作,表示,当两串的第i位字符和第j位字符相等时,将从不包括这两个字符的前缀子串里得到的最长公共子序列+1,得到当前位置的新的最长公共子序列。也就是求解当前i,j的状态,来自于i-1,j-1的状态+1获得。
而当i,j位置的字符不等时,当前位不能延续最长公共子序列的值,只能从之前求得的值中继承。那么我们要求最长的公共子序列,就是要继承所有状态中最大的值,也就是三个位置中选最大值,即i-1,j 和i,j-1和i-1,j-1三个方向取最大值继承。这样递推,每次都使用最大值,继承最大值,延续最大值,将得到的结果也是第lenx,leny处,整个串的最长公共子序列。
于是我们得到状态转移方程:
可以看到,就像之前说的,只有字符相等时,才会有+1的延续,而且只从i-1和j-1处继承,可能你会问,为什么不取3个方向的最大值继承并延续,是因为我们当前匹配成功的是第i和j个字符,那么前i位前缀中已经和前j位前缀得到了一个最大值,前面提到,我们从i-1,j-1位继承,是因为我们第i位与第j位相等了,我们此处一定能算上一个公共的子序列,那么如果除去这个新获得的公共字符,那么就是i-1,j-1的字符串进行比较,只能从没有去i和j的前缀中取一个状态。
如果我们取了i-1,j表示j字符我们已经取到过了,在这个状态中即一个串的前j位和另一个串的前i-1位的最长公共子序列值,那就不存在我们取j位和i位相等的情况了,因为j早就被其他字符所匹配过了。同理i,j-1也是如此,既然这个状态中i已经被配过,新来 j和谁配?明明和i相等,但是i被别的字符给配走了,无法形成一个新的公共字符以增长最长公共子序列值。
总结一下,即增长最长公共子序列只能从i-1,j-1这个状态继承并延续,因为要改变这个状态,需要的是不影响当前匹配状态的上一个状态。 而当不匹配当前字符时,我们选择延续值最大的那个匹配状态,也就是进行i-1,j-1 和i-1,j和j,j-1三选一的操作,因为当前已经不匹配了,我要继续读取新字符检查是否匹配,对于废掉的当前位,我们不需要对上一个状态有什么特殊的要求,因此直接取最大的保留下来即可,为将来可能出现的公共字符提供一个最优解来延续。
就这样递推到字符末尾即可得到两个完整串的最长公共子序列。
#include<stdio.h>///最长公共子序列
#include<string.h>
#include<algorithm>
using namespace std;
int vis[2008][2009],t;
int main()
{
char x[2005];
char y[2004];
while(scanf("%s",x+1)!=EOF)
{
memset(vis,0,sizeof(vis));
int lx=strlen(x+1);
for(int i=1; i<=lx; i++)///回文串子序列,序列中选出一段不连续的子序列使其为回文串
if(x[i]>='a'&&x[i]<='z') x[i]=x[i]-'a'+'A';///将原串倒过来,计算两串的最长公共子序列即最长回文串
int ly=0;
for(int i=lx; i>=1; i--) y[++ly]=x[i];
// printf("%s
%s
",x+1,y+1);
for(int i=1; i<=lx; i++)///边界初始化,当空串和有长度的串比较时,公共子序列长度为0
{
vis[i][0]=0;
}
for(int i=1; i<=ly; i++)
{
vis[0][i]=0;
}
vis[0][0]=0;///空串比较空串
for(int i=1; i<=lx; i++)///dp数组中i和j表示,当一个串长i,另一个串长j时,在此情况下的最长公共子序列
{
for(int j=1; j<=ly; j++)///因此,每次增加一个串的长度i或j,对比其字符是否相相等的情况下说明此字符将延续最长公共子序列,继承i-1,j-1(两串的字符都不取当前字符的最长值)
{///当两当前对比字符相等时,直接从i-1,j-1处的值+1,不从i-1,j和i,j-1处继承
if(x[i]!=y[j])
{///两字符不等时,从三个方向取最大值来继承
vis[i][j]=vis[i-1][j-1];
vis[i][j]=max(vis[i-1][j],max(vis[i][j],vis[i][j-1]));
}
else
vis[i][j]=vis[i-1][j-1]+1;
}
}
// printf(" ");///这是一个很美的动态规划形成的递推表格,想要了解过程的可以解开注释看一下过程
// for (int i=1; i<=lx; ++i)
// printf(" %c",x[i]);
// puts("");
// for(int i=0; i<=ly; i++)
// {
// printf("%c ",i==0?' ':y[i]);
// for(int j=0; j<=lx; j++)
// printf("%d%c",vis[i][j],j==lx?'
':' ');
// }
printf("%d
",ly-vis[lx][ly]);
}
return 0;
}