《DSP using MATLAB》示例Example7.8

       窗函数的设计思想就是选择一个理想的频率选择滤波器（通常其脉冲响应函数是

非因果、无限长的），然后截断（取窗）这个无限长脉冲响应，得到一个线性相位、因果的

FIR滤波器。频率域示意图如下：

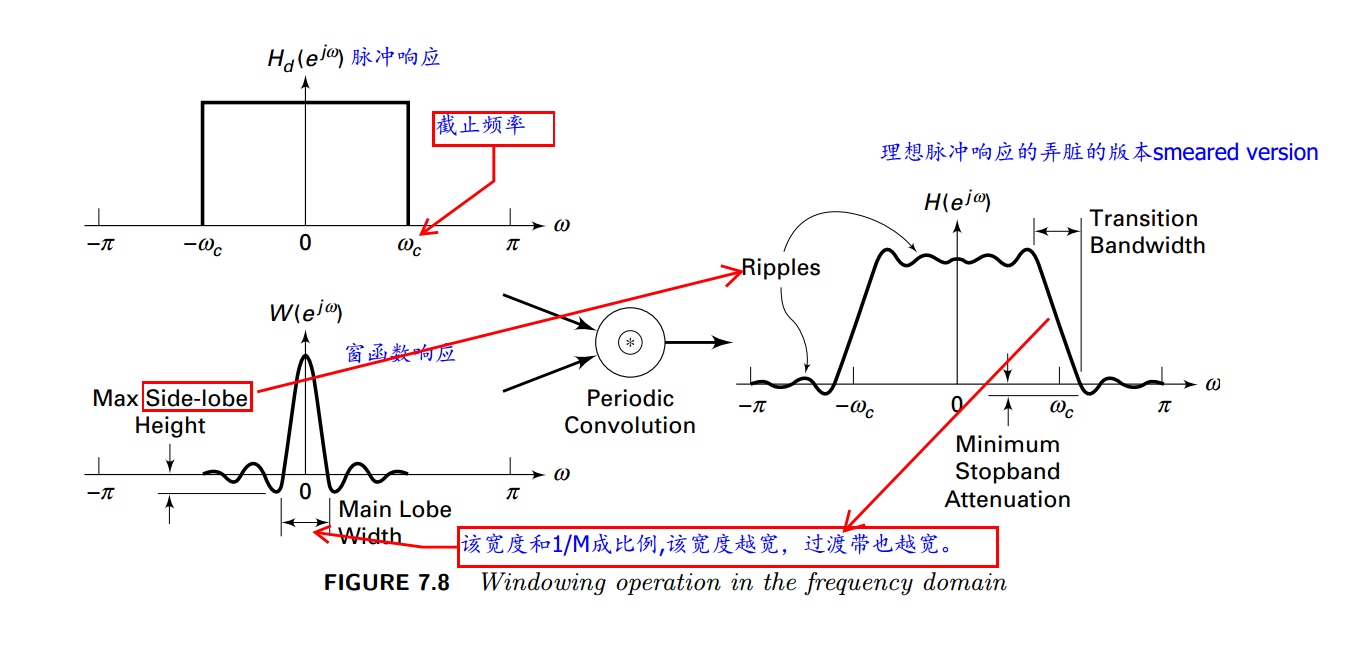
        我们的目的：对于给定的要求，选择滤波器长度M和窗函数ω(n)，该窗函数要有最窄的主瓣宽度和最小的旁瓣衰减。

        前人为我们已经找好了许多窗函数，见下表：

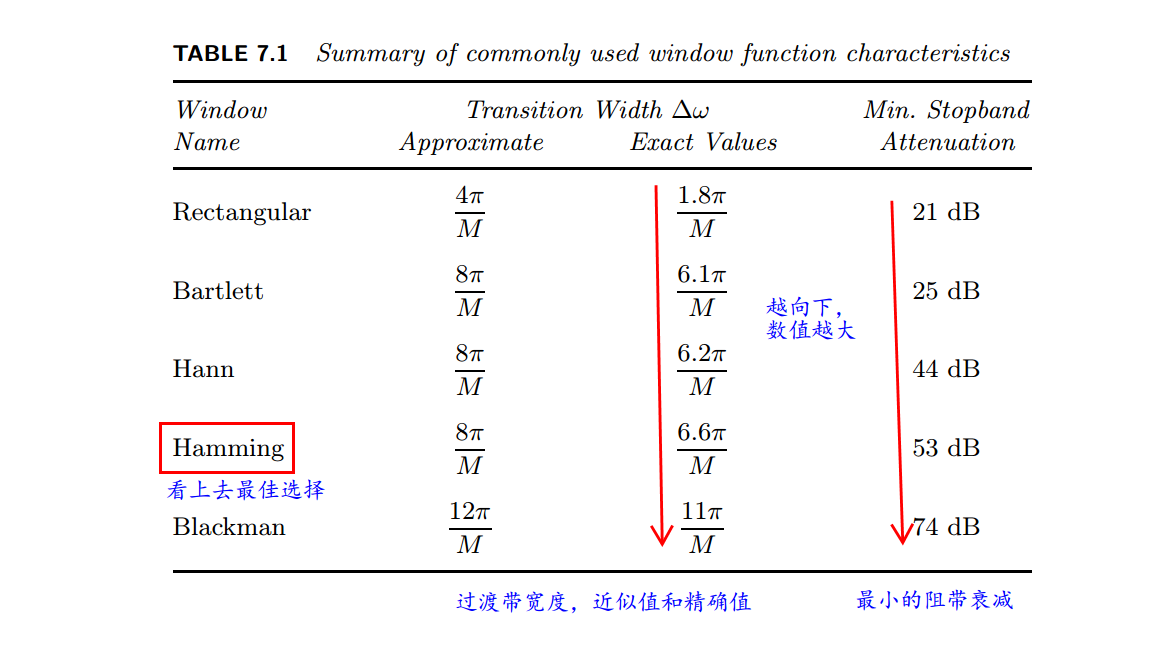
代码：

wp = 0.2*pi; ws = 0.3*pi; tr_width = ws - wp;
M = ceil(6.6*pi/tr_width) + 1

n = [0:1:M-1];
wc = (ws + wp)/2;             % ideal LPF cutoff frequency
hd = ideal_lp(wc, M); w_ham = (hamming(M))';  h = hd .* w_ham;
[db, mag, pha, grd, w] = freqz_m(h, [1]);  delta_w = 2*pi/1000;
Rp = -(min(db(1:1:wp/delta_w+1)))    % Actual Passband Ripple

As = -round(max(db(ws/delta_w+1:1:501)))   % Min Stopband attenuation

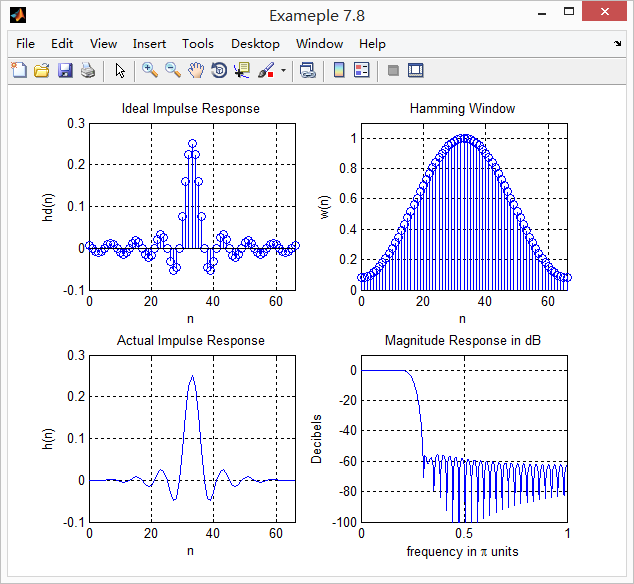
%Plot

figure('NumberTitle', 'off', 'Name', 'Exameple 7.8')
set(gcf,'Color','white'); 

subplot(2,2,1); stem(n, hd); axis([0 M-1 -0.1 0.3]); grid on;
xlabel('n'); ylabel('hd(n)'); title('Ideal Impulse Response');

subplot(2,2,2); stem(n, w_ham); axis([0 M-1 0 1.1]); grid on;
xlabel('n'); ylabel('w(n)'); title('Hamming Window');

subplot(2,2,3); plot(n, h); axis([0 M-1 -0.1 0.3]); grid on;
xlabel('n'); ylabel('h(n)'); title('Actual Impulse Response');

subplot(2,2,4); plot(w/pi, db); axis([0 1 -100 10]); grid on;
xlabel('frequency in pi units'); ylabel('Decibels'); title('Magnitude Response in dB');

　　运行结果：

 

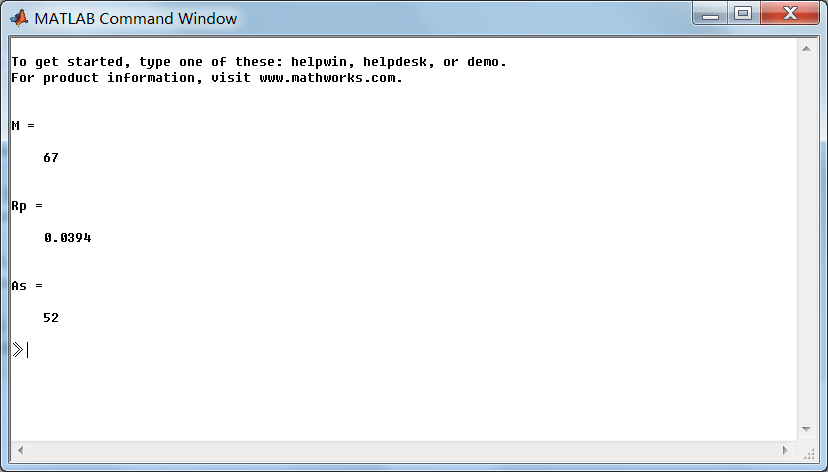
      我们注意到滤波器长度M=67，通带震荡0.0394dB，阻带衰减52dB。满足设计要求。

      代码中求Rp和As的方法强烈推荐，后文经常用到。