函数f(x)用采样间隔Δx=π/5进行采样,使用向前差商、向后差商和中心差商三种公式来近似一阶导数。
书中代码:
%% ------------------------------------------------------------------------------
%% Output Info about this m-file
fprintf('
****************************************************************
');
fprintf('
<FDTD 4 ElectroMagnetics with MATLAB Simulations>
');
fprintf('
Figure 1.2
');
time_stamp = datestr(now, 31);
[wkd1, wkd2] = weekday(today, 'long');
fprintf(' Now is %20s, and it is %7s
', time_stamp, wkd2);
%% ------------------------------------------------------------------------------
% Create exact function and its derivative
N_exact = 301; % number of sample points for exact function
x_exact = linspace(0, 6*pi, N_exact);
f_exact = sin(x_exact) .* exp(-0.3*x_exact);
f_derivative_exact = cos(x_exact) .* exp(-0.3*x_exact) - 0.3*sin(x_exact).*exp(-0.3*x_exact);
% plot exact function
figure('NumberTitle', 'off', 'Name', 'Figure 1.2.a');
set(gcf,'Color','white');
plot(x_exact, f_exact, 'k-', 'linewidth', 1.5);
set(gca, 'fontsize', 12, 'fontweight', 'demi');
axis([0 6*pi -1 1]); grid on;
xlabel('$x$', 'interpreter', 'latex', 'fontsize', 16);
ylabel('$f(x)$', 'interpreter', 'latex', 'fontsize', 16);
title('Exact function');
% create exact function for pi/5 sampleing peroid and
% its finite difference derivatives
N_a = 31; % number of points for pi/5 sampling period
x_a = linspace(0, 6*pi, N_a); % [0, 6pi], row vector with 31 points
f_a = sin(x_a) .* exp(-0.3*x_a);
f_derivative_a = cos(x_a) .* exp(-0.3*x_a) - 0.3*sin(x_a) .* exp(-0.3*x_a);
dx_a = pi/5;
f_derivative_forward_a = zeros(1, N_a); % 1×31 zero matrix
f_derivative_backward_a = zeros(1, N_a);
f_derivative_central_a = zeros(1, N_a);
f_derivative_forward_a(1:N_a-1) = (f_a(2:N_a)-f_a(1:N_a-1))/dx_a;
f_derivative_backward_a(2:N_a) = (f_a(2:N_a)-f_a(1:N_a-1))/dx_a;
f_derivative_central_a(2:N_a-1) = (f_a(3:N_a)-f_a(1:N_a-2))/(2*dx_a);
% create exact function for pi/10 sampleing peroid and
% its finite difference derivatives
N_b = 61; % number of points for pi/10 sampling period
x_b = linspace(0, 6*pi, N_b);
f_b = sin(x_b) .* exp(-0.3*x_b);
f_derivative_b = cos(x_b) .* exp(-0.3*x_b) - 0.3*sin(x_b) .* exp(-0.3*x_b);
dx_b = pi/10;
f_derivative_forward_b = zeros(1, N_b);
f_derivative_backward_b = zeros(1, N_b);
f_derivative_central_b = zeros(1, N_b);
f_derivative_forward_b(1:N_b-1) = (f_b(2:N_b)-f_b(1:N_b-1))/dx_b;
f_derivative_backward_b(2:N_b) = (f_b(2:N_b)-f_b(1:N_b-1))/dx_b;
f_derivative_central_b(2:N_b-1) = (f_b(3:N_b)-f_b(1:N_b-2))/(2*dx_b);
% plot exact derivative of the function and its finite difference
% derivatives using pi/5 sampling period
figure('NumberTitle', 'off', 'Name', 'Figure 1.2.b');
set(gcf,'Color','white');
plot(x_exact, f_derivative_exact, 'k', ...
x_a(1:N_a-1), f_derivative_forward_a(1:N_a-1), 'b--', ...
x_a(2:N_a), f_derivative_backward_a(2:N_a), 'r-.', ...
x_a(2:N_a-1), f_derivative_central_a(2:N_a-1), ':ms', ...
'markersize', 4, 'linewidth', 1.5);
set(gca, 'fontsize', 12, 'fontweight', 'demi');
axis([0 6*pi -1 1]); grid on;
legend('exact', 'forward difference', 'backward difference', 'central difference');
xlabel('$x$', 'interpreter', 'latex', 'fontsize', 16);
ylabel('$f''(x)$', 'interpreter', 'latex', 'fontsize', 16);
text(pi, 0.6, '$Delta x = pi/5$', 'interpreter', 'latex', 'fontsize', 16, 'backgroundcolor', ...
'w', 'edgecolor', 'k');
% plot error for finite difference derivatives
% using pi/5 sampling period
error_forward_a = f_derivative_a - f_derivative_forward_a;
error_backward_a = f_derivative_a - f_derivative_backward_a;
error_central_a = f_derivative_a - f_derivative_central_a;
figure('NumberTitle', 'off', 'Name', 'Figure 1.2.c');
set(gcf,'Color','white');
plot(x_a(1:N_a-1), error_forward_a(1:N_a-1), 'b--', ...
x_a(2:N_a), error_backward_a(2:N_a), 'r--', ...
x_a(2:N_a-1), error_central_a(2:N_a-1), ':ms', ...
'markersize', 4, 'linewidth', 1.5);
set(gca, 'fontsize', 12, 'fontweight', 'demi');
axis([0 6*pi -0.2 0.2]); grid on;
legend('forward difference', 'backward difference', 'central difference');
xlabel('$x$', 'interpreter', 'latex', 'fontsize', 16);
ylabel('error $[f''(x)]$' , 'interpreter', 'latex', 'fontsize', 16);
text(pi, 0.15, '$Delta x = pi/5$', 'interpreter', 'latex', 'fontsize', 16, ...
'backgroundcolor', 'w', 'edgecolor', 'k');
% plot error for finite difference derivatives
% using pi/10 sampling period
error_forward_b = f_derivative_b - f_derivative_forward_b;
error_backward_b = f_derivative_b - f_derivative_backward_b;
error_central_b = f_derivative_b - f_derivative_central_b;
figure('NumberTitle', 'off', 'Name', 'Figure 1.2.d');
set(gcf,'Color','white');
plot(x_b(1:N_b-1), error_forward_b(1:N_b-1), 'b--', ...
x_b(2:N_b), error_backward_b(2:N_b), 'r-.', ...
x_b(2:N_b-1), error_central_b(2:N_b-1), ':ms', ...
'markersize', 4, 'linewidth', 1.5);
set(gca, 'fontsize', 12, 'fontweight', 'demi');
axis([0 6*pi -0.2 0.2]); grid on;
legend('forward difference', 'backward difference', 'central difference');
xlabel('$x$', 'interpreter', 'latex', 'fontsize', 16);
ylabel('error $[f''(x)]$' , 'interpreter', 'latex', 'fontsize', 16);
text(pi, 0.15, '$Delta x = pi/10$' , 'interpreter', ...
'latex', 'fontsize', 16, 'backgroundcolor', 'w', 'edgecolor', 'k' );
运行结果:

上图是函数图形,看出振幅是指数衰减的。下图是一阶导数的精确值(公式计算)和三种差商近似结果。中心差商近似结果接近
精确值。

下图是在Δx=π/5采样间隔下,三种差商近似与精确值之间的误差对比。可以看出中心差商近似的误差最小。

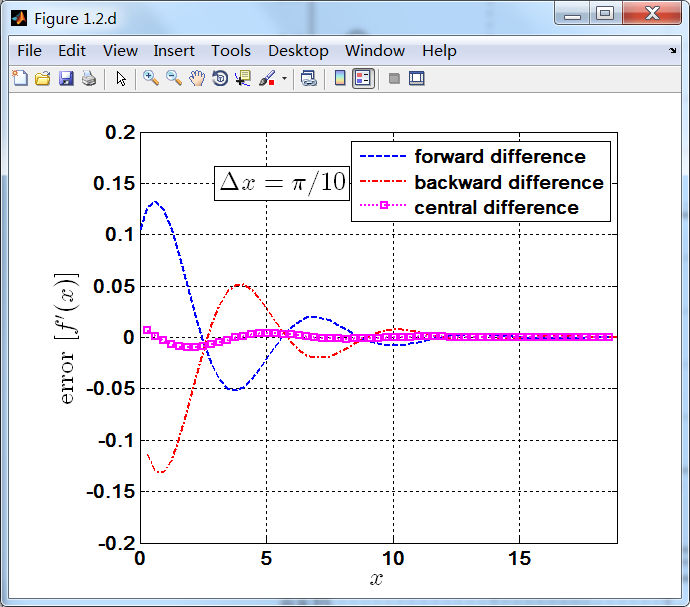
下图是Δx=π/10采样间隔下,三种差商近似与精确值之间的误差对比。可以看出中心差商近似的误差最小。另外由于向前差商和
向后差商近似是1阶精度,中心差商近似是2阶精度,所以采样间隔由π/5变成π/10后,向前差商和向后差商近似误差变为原来的二分之一,
而中心差商近似误差变为原来的四分之一。