证明过程:


代码:
%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
%% Output Info about this m-file
fprintf('
***********************************************************
');
fprintf(' <DSP using MATLAB> Problem 5.37
');
banner();
%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
% -------------------------------------------------------------------------------------
% X(k) is DFTs of real-valued sequence x(n)
% x(n)=A*cos(wn)R(n) n=[0:N-1]
%
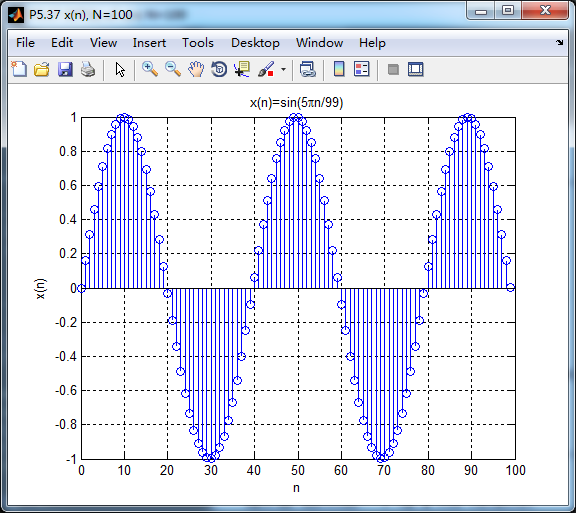
% x(n) = sin(5*pi*n/99) n=[0:100-1]
% -------------------------------------------------------------------------------------
N = 100; A = 1;
n1 = [0:N-1];
x1 = A*sin(5*pi*n1/99);
figure('NumberTitle', 'off', 'Name', 'P5.37 x(n), N=100')
set(gcf,'Color','white');
stem(n1, x1);
xlabel('n'); ylabel('x(n)');
title('x(n)=sin(5pin/99)'); grid on;
k1 = [0:N-1];
Xk_DFT = fft(x1, N);
N1 = length(Xk_DFT); % length
magXk_DFT = abs( [ Xk_DFT ] ); % DFT magnitude
angXk_DFT = angle( [Xk_DFT] )/pi; % DFT angle
realXk_DFT = real(Xk_DFT); imagXk_DFT = imag(Xk_DFT);
figure('NumberTitle', 'off', 'Name', 'P5.37 X(k), DFT of x(n) N=100')
set(gcf,'Color','white');
subplot(2,1,1); stem(k1, magXk_DFT);
xlabel('k'); ylabel('magnitude(k)');
title('magnitude DFT of x(n)'); grid on;
subplot(2,1,2); stem(k1, angXk_DFT);
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel('k'); ylabel('angle(k)');
title('angle DFT of x(n)'); grid on;
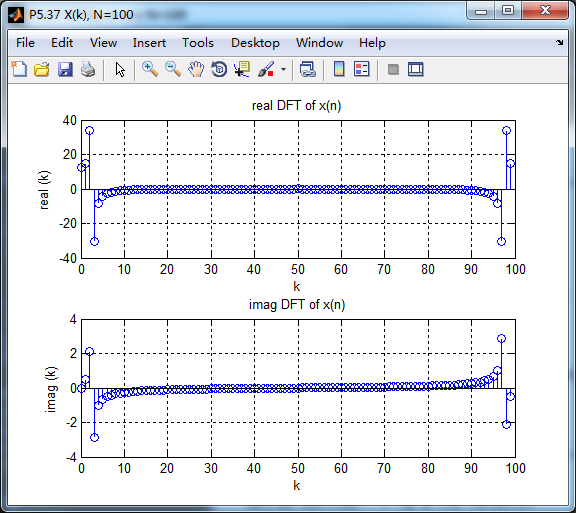
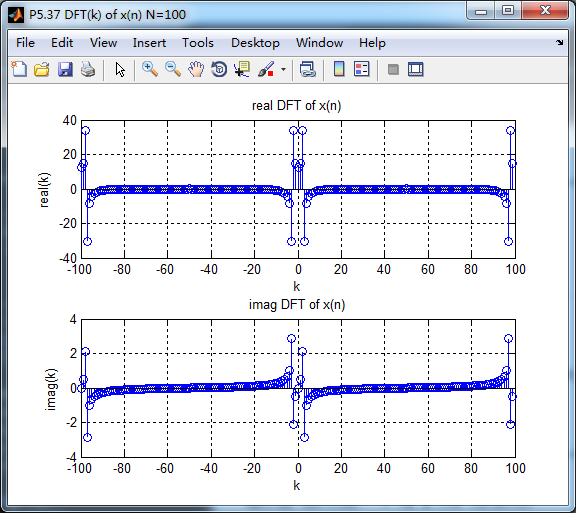
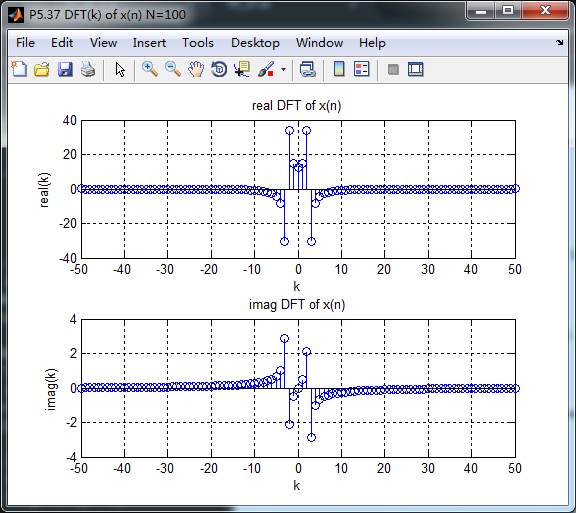
figure('NumberTitle', 'off', 'Name', 'P5.37 X(k), N=100')
set(gcf,'Color','white');
subplot(2,1,1); stem(k1, realXk_DFT);
xlabel('k'); ylabel('real (k)');
title('real DFT of x(n)'); grid on;
subplot(2,1,2); stem(k1, imagXk_DFT);
%axis([-N/2, N/2, -0.5, 50.5]);
xlabel('k'); ylabel('imag (k)');
title('imag DFT of x(n)'); grid on;
运行结果:
原始序列
不同范围的DFT