LC 494. Target Sum

问题描述

You are given a list of non-negative integers, a1, a2, ..., an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

Example 1:

Input: nums is [1, 1, 1, 1, 1], S is 3. 
Output: 5
Explanation: 

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

There are 5 ways to assign symbols to make the sum of nums be target 3.

Note:

1. The length of the given array is positive and will not exceed 20.
2. The sum of elements in the given array will not exceed 1000.
3. Your output answer is guaranteed to be fitted in a 32-bit integer.

参考答案

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int s) {
        int sum = accumulate(nums.begin(), nums.end(), 0);
        return sum < s || (s + sum) & 1 ? 0 : subsetSum(nums, (s + sum) >> 1); 
    }   

    int subsetSum(vector<int>& nums, int s) {
        int dp[s + 1] = { 0 };
        dp[0] = 1;
        for (int n : nums)
            for (int i = s; i >= n; i--)
                dp[i] += dp[i - n];
        return dp[s];
    }
};

答案解释

1. （s+sum) & 1 是什么?

通过 &1 操作，检查(s+sum) 是否可以被2整除，只有被整除的数字，才可以继续运算。

2. (s+sum)>>1 是什么?

除以 2 的操作

3. 为什么要有以上操作？

根据 这个论坛 的解释：

　　　　　　　　　　　　  sum(P) - sum(N) = target

　　　　sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)

　　　　　　　　　　　　　　    2 * sum(P) = target + sum(nums)

s+sum 需要被 2 整除。

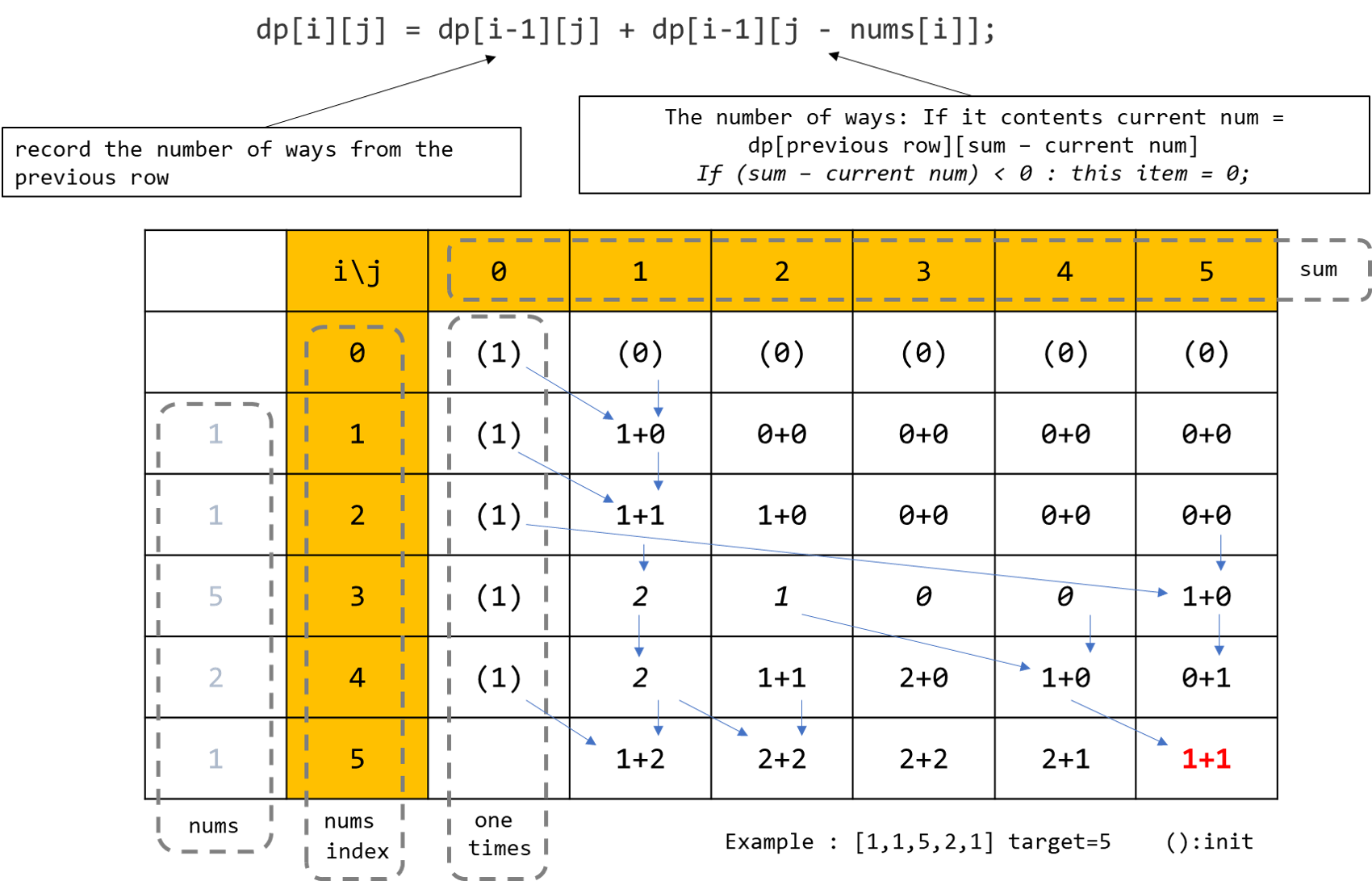
4. subsetSum 是什么函数？

原理，如下图所示（原创）：