题目描述
某个国家有n个城市,这n个城市中任意两个都连通且有唯一一条路径,每条连通两个城市的道路的长度为zi(zi<=1000)。这个国家的人对火焰有超越宇宙的热情,所以这个国家最兴旺的行业是消防业。由于政府对国民的热情忍无可忍(大量的消防经费开销)可是却又无可奈何(总统竞选的国民支持率),所以只能想尽方法提高消防能力。
现在这个国家的经费足以在一条边长度和不超过s的路径(两端都是城市)上建立消防枢纽,为了尽量提高枢纽的利用率,要求其他所有城市到这条路径的距离的最大值最小。
你受命监管这个项目,你当然需要知道应该把枢纽建立在什么位置上。
输入输出格式
输入格式:
输入包含n行:
第1行,两个正整数n和s,中间用一个空格隔开。其中n为城市的个数,s为路径长度的上界。设结点编号以此为1,2,……,n。
从第2行到第n行,每行给出3个用空格隔开的正整数,依次表示每一条边的两个端点编号和长度。例如,“2 4 7”表示连接结点2与4的边的长度为7。
输出格式:
输出包含一个非负整数,即所有城市到选择的路径的最大值,当然这个最大值必须是所有方案中最小的。
输入输出样例
输入样例#1: 复制
5 2
1 2 5
2 3 2
2 4 4
2 5 3
输出样例#1: 复制
5
输入样例#2: 复制
8 6
1 3 2
2 3 2
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3
输出样例#2: 复制
5
说明
【数据规模和约定】
对于20%的数据,n<=300。
对于50%的数据,n<=3000。
对于100%的数据,n<=300000,边长小等于1000。
Solution
显然,我们选的在直径上是最优的(简单证明:假设我们选7-6(长度为6),还不如只选7-4(长度为2),因为还可以留下多余长度去选更多的点,为什么说还不如只选7-4呢?因为4-6长度不可能大于4-2的长度,因为2是直径的上的点),把样例2直径画出来,如下图:
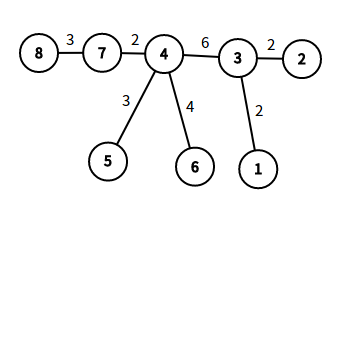
2 3 4 7 8为直径,接下来我们就可以用尺取法贪心在直径上求出很多条长度小于等于s的路径,根据图,我们可以选出8-4长度为5,4-3长度为6,3-2长度为2这些路径。当我们选8-4时,显然2点离选的路径最远也就是直径的一端,显然1,5,6这三个不在直径上的点不会比直径的一端2点离选的这条路径更远,因为如果更远的话,说明之前求得不是树上最长路,也就是不是直径。同理,我们先不需考虑不在直径上的点。但是我们在最后还是需要考虑不是在直径上的点,例如样例2的s为inf,也就是可以选无限长,那么我们可以选直径2 3 4 7 8,如果我们不考虑不在直径上的点,那么答案为0,显然答案为4(4点到6点距离),我们只需求出不在直径上的点离直径有多远就行了。
时间复杂度 O(n)
代码如下:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int fa[310100],vis[301000],last[301000],len=0,d[301000];
struct node
{
int to,next,w;
}a[601000];
void add(int a1,int a2,int a3)
{
len++;
a[len].to=a2;
a[len].w=a3;
a[len].next=last[a1];
last[a1]=len;
}
void dfs(int x)
{
for(int i=last[x];i;i=a[i].next)
{
int to=a[i].to;
if(vis[to]||fa[x]==to) continue;
fa[to]=x;
d[to]=d[x]+a[i].w;
dfs(to);
}
}
int main()
{
int n,s,x,y,z,ans=2147483647;
cin>>n>>s;
for(int i=1;i<n;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
int l=1,r=1;
dfs(l);
for(int i=1;i<=n;i++)
if(d[i]>d[l]) l=i;
memset(fa,0,sizeof(fa));
d[l]=0;dfs(l);
for(int i=1;i<=n;i++)
if(d[i]>d[r]) r=i;
int t=r;
//cout<<r<<endl;
//cout<<d[r]<<endl;
for(int i=r;i;i=fa[i])//尺取法
{
while(fa[t]&&d[i]-d[fa[t]]<=s) t=fa[t];
ans=min(ans,max(d[t],d[r]-d[i]));
}
for(int i=r;i;i=fa[i]) vis[i]=1;
for(int i=r;i;i=fa[i]) d[i]=0,dfs(i);
for(int i=1;i<=n;i++)
if(!vis[i])
ans=max(ans,d[i]);
cout<<ans;
}