本文主要讨论基于求最小生成树的两种算法—Prim算法和Kruskal算法
主要说说其思想,附代码解释,有问题请留言
延时的Prim算法
- 思想:每一步为最小生成树的成长增加一条最短的边。
分析:
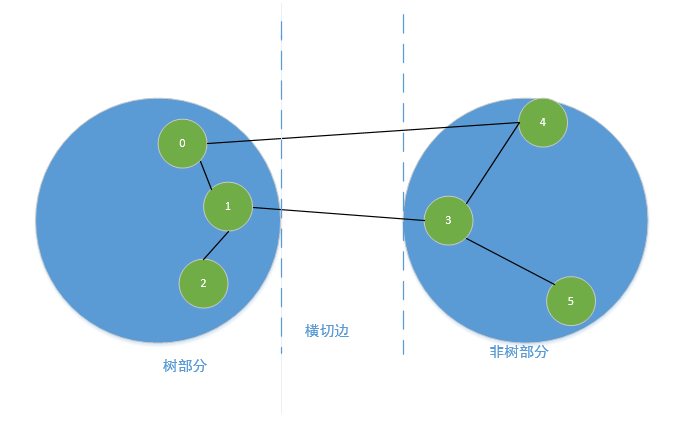
1>将所有的顶点分为两部分,一部分是逐渐生长的最小生成树(可以用队列来存储),一部分是逐渐减少的非最小生成树(用marked来标记);
2>还有一个队列维护的边,自然就是存放连接这两部分的边(横切边),每次生长,都在横切边的队列中,取出最小的边加入到最小生成树中;
3>加入某个顶点和边之后,相应的修改横切边的队列(因为树和非树已经发生变化)。 - 如图:
- 代码
注:代码中所使用到的MinPQ类没有什么特别的,就是提供最小值的优先队列数据结构。
package minSpanningTree;
import java.util.LinkedList;
import java.util.Queue;
/**
*延时的Prim算法,维护两个队列和一个布尔型数组
*<p>横切边队列:用于维护最小生成树和非最小生成树两个部分之间的连线,
*并为最小生成树生成横切边的最小值,加入到最小生成树中
*<p>布尔型数组则是最小生成树的生长过程路迹
* @author luoz
* @date 2016年9月21日 下午10:24:54
**/
public class LazyPrinmMST {
private MinPQ<Edge> pq; //横切边队列
private Queue<Edge> tree; //最小生成树队列
private boolean[] marked; //最小生成树的顶点
/**
* 传入无向带权值图g,构造最小生成树序列
* @param g
*/
public LazyPrinmMST(EdgeGraph g)
{
/*初始化*/
marked = new boolean[g.V()];
tree = new LinkedList<Edge>();
pq = new MinPQ<>();
/*从0顶点开始,增加所有与0顶点相连的所有边到pq队列中*/
visit(g,0);
/*只要还有一个顶点未被标记的边,就继续将那个顶点以及其与最小生成树最小的横切边加入到最小生成树中*/
while(!pq.isEmpty())
{
/*每一步都为最小生成树增加一个横切边的最小值*/
Edge e = pq.delMin();
/*分析最小横切边*/
int v = e.either();
int w = e.other(v);
/*若两个顶点均是被标记了的,此边为无效边*/
if(marked[v] && marked[w])
continue;
/*否则加入到最小生成树的队列中*/
tree.add(e);
/*加入一条边后,因为最小生成树和非最小生成树两个部分都已经变化,所以也需要更新横切边队列,*/
if(!marked[v])
visit(g,v);
if(!marked[w])
visit(g,w);
}
}
/**
* 维护横切边队列
* 传入参数无向带权值图g,访问到的顶点v
* @param g
* @param v
*/
private void visit(EdgeGraph g,int v)
{
marked[v] = true; //标记顶点为已访问
/**
* 因为在最小生成树中,每生成一个顶点就需要将其顶点的所有边
* 其中一个顶点已经被标记了的边就不需要添加,因为这条边的两个顶点均在最小生成树中
* */
for(Edge e : g.adj(v))
if(!marked[e.other(v)])
pq.insert(e);
}
/*输出最小生成树的序列*/
public Iterable<Edge> tree()
{
return tree;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Edge e1 = new Edge(0,1,100);
Edge e2 = new Edge(0,1,200);
Edge e3 = new Edge(0,2,300);
Edge e4 = new Edge(0,2,400);
EdgeGraph g = new EdgeGraph(3);
g.addEdge(e1);
g.addEdge(e2);
g.addEdge(e3);
g.addEdge(e4);
LazyPrinmMST l = new LazyPrinmMST(g);
System.out.println(l.tree());
}
}
即时的Prim算法
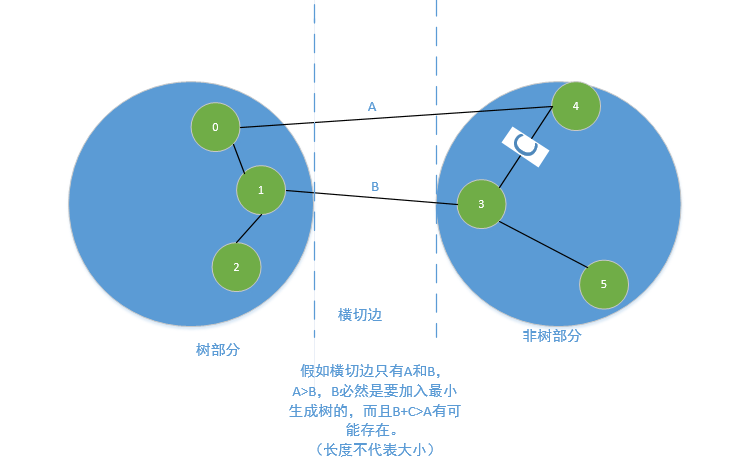
- 思想:由延时的Prim算法我们可以知道,MinPQ队列保存了所有的横切边,但是实际上我们真正需要的不可能是所有的横切边,相反,我们对于横切边的1最小值,我们是肯定要加入到最小生成树中的(即使是延时版本中)
- 如图:
- 代码:
package minSpanningTree;
import java.util.LinkedList;
import java.util.Queue;
/**
*最小生成树的Prim算法即时实现:由Prim算法的延时实现可以知道,主要是把全部的顶点
*看为两个部分:最小生成树部分和非最小生成树部分。在维护横切边队列的同时,保存了所有两个部分相连的边
*<p>在即时版本中,我们维护了两个数组和一个队列,还有一个布尔型数组
*<p>队列中只维护了两个部分相连的最小的边,因为即使在延时版本中,这条最小的边也必然迟早会加入到最小生成树中
*<p>同时增加了一个Edge数组,保存不断增长的最小边(树),
*一个Double数组保存权重,用于不断比较树和非树的更短边,并将更短边不断更新到Edge数组中
*
* @author luoz
* @date 2016年9月22日 下午3:28:10
**/
public class PrimMST {
private boolean[] marked; //边在树中则为true
private IndexMinPQ<Double> pq; //有效的横切边
private Edge[] edgeTo; //距离最小生成树最近的边
private double[] distTo; //distTo[w] = edgeTo[w].weight()
public PrimMST(EdgeGraph g)
{
marked = new boolean[g.V()];
pq = new IndexMinPQ<Double>(g.V());
edgeTo = new Edge[g.V()];
distTo = new double[g.V()];
/*将每一个顶点距离树的距离都初始化为无穷大*/
for(int i = 0;i<g.V();i++)
distTo[i] = Double.POSITIVE_INFINITY;//double POSITIVE_INFINITY = 1.0 / 0.0
distTo[0] = 0.0;
pq.insert(0,0.0);
while(!pq.isEmpty())
{
//延时实现是对每一条不在树中的边都进行维护,在即时实现中,只对最小权值的边进行维护
visit(g,pq.delMin());
}
}
private void visit(EdgeGraph g,int v)
{
marked[v] = true;
/*循环每一个与v顶点(也可以看作是树)相连的边,得出最短的边并加入到队列pq中*/
for(Edge e :g.adj(v))
{
int w = e.other(v);
//marked[v]已经被标记true了
if(marked[w])
continue;
/*distTo初始为无穷大,循环过程中,不断地更新与顶点v最近的边*/
if(e.weight() < distTo[w])
{
//连接树的边也要增加或者是修改
edgeTo[w] = e;
distTo[w] = e.weight();
/*发现了更小的边,假如这个边的顶点,已经包含在队列中,那么就更新这个顶点的边的最小值,否则加入到队列中*/
if(pq.contains(w)) //可能两个顶点存在两条不同权值的边
pq.change(w, distTo[w]);
else
pq.insert(w, distTo[w]);
}
}
}
public Iterable<Edge> edges() {
Queue<Edge> mst = new LinkedList<Edge>();
for (int v = 0; v < edgeTo.length; v++) {
Edge e = edgeTo[v];
if (e != null) {
mst.add(e);
}
}
return mst;
}
public double weight() {
double weight = 0.0;
for (Edge e : edges())
weight += e.weight();
return weight;
}
}
Kruskal算法
- 思想:每次取所有边中的一个最小值加入到最小生成树中,直到所有顶点都在树中为止。
分析:Prim算法可以说是范围由小到大,因为,Prim算法是将所有顶点分为树和非树部分,树部分不断增长;而Kruskal算法一开始就是对所有顶点所有边进行筛选,在其中选出最小值加入到树中,自然是由稀疏到密集。
2.代码:
package minSpanningTree;
import java.util.LinkedList;
import java.util.Queue;
/**
*Kruskal算法主要思想:一次性就将全部的边加入到队列中,然后依次按照权值处理它们
*最小生成树就是依次取最小值,每次取值,查看该边是否有效(即两个顶点是否都在树中)
* @author luoz
* @date 2016年9月22日 下午4:42:46
**/
public class KruskalMST {
//生出的树的队列
private Queue<Edge> mst;
//最小生成树的权值和
private double weight;
public KruskalMST(EdgeGraph g)
{
mst = new LinkedList<Edge>();
//初始化一个队列(MinPQ,主要用于求出队列中的最小值的边1)
MinPQ<Edge> pq = new MinPQ<Edge>();
//将所有边加入到队列中
for (Edge e : g.edges()) {
pq.insert(e);
}
//这个并不特殊,UF类是一个检测顶点是否有相连的类
UF uf = new UF(g.V());
//判断条件自然是队列为空,并且确认所有的顶点都加入到了mst队列中
while(!pq.isEmpty() && mst.size() < g.V()-1)
{
Edge e = pq.delMin();
int v = e.either();
int w = e.other(v);
//判断v,w两个顶点是否已经相连,因为最开始的两个顶点,必然是没有相连的。(相连意味着已经加入到mst中了)
if(uf.connected(v, w))
continue;
uf.union(v, w);
mst.add(e);
weight += e.weight();
}
}
public Iterable<Edge> edges()
{
return mst;
}
public double weight()
{
return weight;
}
}
附加代码
MinPQ.java,IndexMinPQ.java:http://algs4.cs.princeton.edu/20sorting/
UF.java:http://algs4.cs.princeton.edu/10fundamentals/