本篇文章主要介绍2-3树,并由2-3树重点介绍RB树(红黑树)
后附完整代码
2-3树
1. 2-3树
2-3树概念:
一颗2-3查找树,或为空树,或为由2-结点,3-结点构成的树。
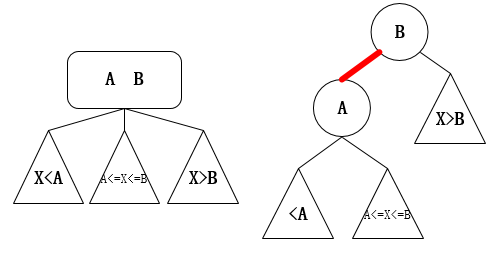
2-结点:含有一个键值对和两个链接,左链接的结点均小于该结点,右链接的结点均大于该结点。
3-结点:含有两个键值对和三个链接,左链接的结点小于该节点的小的键值,中链接介于该结点的两个键值之间,右链接大于改结点的大的键值。
2. 2-3树的查找添加
1).查找:
参照上一篇文章,实现较为简单,即比较需要查找的key值和x.left,x.right比较,递归实现。
2).添加:
添加首先需要查找添加到的正确位置;
然后主要两类(其他都可以由这两个变换出):
一:添加到空结点—直接添加,或者向2-结点添加(2-结点变为3-结点实现);
二:向3-结点的树增加新键值,1.创建一个4-结点,2.将4-结点分解为两个2-结点树;
<如向一个父结点为3-结点的3-结点添加新键值,同样先变为4-结点,再递归往上变为3-结点,若递归到跟结点仍为4-结点,则直接分解根结点>
红黑树
红黑树背后的基本思想是用标准的二叉查找树(完全由2-结点构成),和一些额外的信息(红链接表示3-结点,黑链接表示2-3树的普通链接)。
在阅读本文前,要摆脱的思想是,红链接并非是一个2-结点所有的,一个红链接,它是两个2-结点构成的。
因此下文所说到的红链接,其实就是两个2-结点,一个3-结点,其实也就是一个红链接,而并非Node结构中多出Mid引用!
(而4-结点呢?自然就是两个红色链接了)
1.红黑树定义
其中,其满足以下三个含有红黑链的二叉查找树:
1>红链接均为左链接;
2>没有任何一个结点是同时由两个红链接组成;
3>该树是完美黑色平衡(即:任意空链接到根结点路径上的黑链接数目相同)。
红黑树的添加
红黑树和2-3树?
如图:
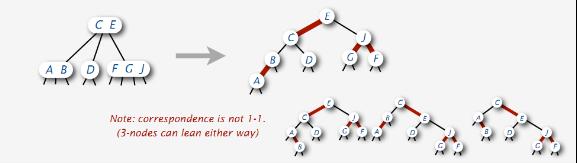
是不是很有关系了。
为什么会有红黑树的旋转操作?为什么会有左右旋转和颜色转换?
因为必须保证树是完美黑色平衡的。
所以在涉及红黑树的操作,如增加时:
我们必须保证刚刚增加的结点的链接颜色是红色的。(这样递归增加这样的结点时候,树就是红黑树了)
假如我们刚刚增加的结点是大于根结点的,这个时候就需要用到左旋转了。
而右旋转则是因为存在两条连续的红色左链接,所以这时候需要右旋转后再左旋转。
红黑树的旋转
正是因为有了两个变换过程,所以保证了红黑树的前两个定义。
而第三个颜色转换,使得对于红黑树来说,红链接更少,而黑链接更多,从而大大提高效率。(因为增加删除都是对于红链接操作的,这就是红黑树效率高于AVL树的原因之一)
1).左旋转
存在右边链接为红色的结点。
实现如下:
private Node rotateLeft(Node h)
{
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
x.N = h.N;
h.N = size(h.left) + size(h.right)+1;
return x;
}2).右旋转
存在两条连续的左链接为红色。
如:x.left = RED && x.left.left = RED;
实现:
private Node rotateRight(Node h)
{
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = h.color;
h.color = RED;
x.N = h.N;
h.N = size(h.left) + size(h.right)+1;
return x;
}3).颜色转换
// flip the colors of a node and its two children
private void flipColors(Node h) {
// h must have opposite color of its two children
// assert (h != null) && (h.left != null) && (h.right != null);
// assert (!isRed(h) && isRed(h.left) && isRed(h.right))
// || (isRed(h) && !isRed(h.left) && !isRed(h.right));
h.color = !h.color;
h.left.color = !h.left.color;
h.right.color = !h.right.color;
}以下是三个变换过程:
添加操作put实现:
private Node put(Node h, Key key, Value val)
{
//Recursive comparison the node insertion location
//添加的结点,显然是要设置为红色
if (h == null)
return new Node(key, val, 1, RED);
int cmp = key.compareTo(h.key);
if (cmp < 0)
h.left = put(h.left, key, val);
else if (cmp > 0)
h.right = put(h.right, key, val);
else
h.val = val;
//每一次递归增加元素,都需要修复红黑树,以保证三个定义.
// fix-up any right-leaning links
if (isRed(h.right) && !isRed(h.left))
h = rotateLeft(h);
if (isRed(h.left) && isRed(h.left.left))
h = rotateRight(h);
if (isRed(h.left) && isRed(h.right))
flipColors(h);
h.N = size(h.left) + size(h.right) + 1;
return h;
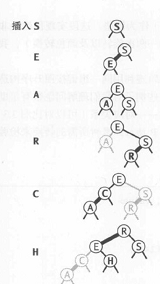
}如下图过程:
红黑树删除
删除操作时,我们必须保证删除的不是2-结点,因为2-结点删除后形成一个空链接,从而破坏了红黑树的第三个定义。
1. 2-3-4树的插入算法
<此算法实现沿路径既能向上也能向下进行变换的操作>
分为两部分:
1>向下变换
保证当前结点不是4-结点,当遇到父结点为2-结点的4-结点,将4-结点分为两个2-结点,并且将中间键值传给父结点(父结点变为3-结点); 当遇到父结点为3-结点的4-结点,同样将上一操作(此时父结点变为4-结点——用向上变换摊平)。
2>向上变换
将之前创建的4-结点配平(分解为三个2-结点,高度增加1)。
此算法在红黑树上的实现:
1>将4-结点分解为三个2-结点子树,用红链接连接起来;
2>向下过程(递归过程)将所有4-结点进行颜色转换;
3>向上过程,分解旋转分解所有4-结点(配平)。
2. 删除最小键
由红黑树的第三个定义可以知道,删除键时,假如删除的是2-结点,会形成一个空链接,从而导致第三个定义不符合。因此,删除红黑树键时,当前结点必须是3-结点(即:只能在红链接中删除)。
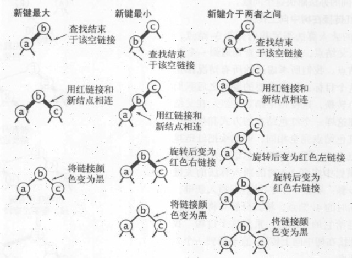
完成以上要求的,必须满足一下情况之一:
1>假如当前结点不是2-结点;
2>当前结点的左子结点是2-结点,而当前结点的兄弟结点不是2-结点,此时需要借一个结点进行删除操作;
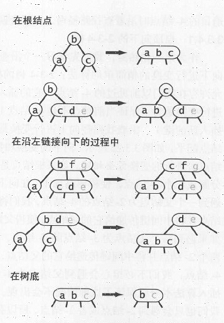
3>如果当前结点的左结点和它的亲兄弟结点都是2-结点,则将左子结点,父结点中的最小键和左子结点最近的兄弟结点合并为一个4-结点,使得父结点由3-结点变为2-结点或者由4-结点变为3-结点。
(如下图的第四个变换)
三个过程如下图:
实现如下:
public void deleteMin()
{
if(!isRed(root.left) && !isRed(root.right))
root.color = RED;
root = deleteMin(root);
if(!isEmpty())
root.color = BLACK;
}
private Node deleteMin(Node h)
{
//最开始递归由上至下是吧,即由树根到叶子的过程
if(h.left == null)
//可能有人会疑问,为什么递归结束条件不是h == null.
//因为是不存在h,和h.right的这样两个结点的子树.
return null;
/**
* 既然知道了h.left==null,
* 是不是这个时候我们就要看一下h这个结点是不是3-结点或者是4-结点呢,
* 因为前面已经说过,我们的删除操作是必须要在非2-结点中进行
*/
if(!isRed(h.left) && !isRed(h.left.left))
h = moveRedLeft(h);
h.left = deleteMin(h.left);
//下面这个balance自然就是向上使用旋转配平啦
return balance(h);
}其中moveRedLeft如下:
private Node moveRedLeft(Node h)
{
/**filpColors?为什么呢?
*因为我们不是要构造3-结点或者4-结点的吗
*而此时我们也不要忘了,递归是由上至下的
*所以filpColors构造依次构造临时4-结点罢了
*/
flipColors(h);
/**
* 别忘了deleteMin的if判断语句
* 它只是判断了h.left && h.left.left两个结点false(null也是false)
* 所以呢,最小值可能存在于h的右子树当中吧
* 因此呢,对于右子树,我们也是要配4-结点的
*/
if(isRed(h.right.left))
{
h.right = rotateRight(h.right);
h = rotateLeft(h);
}
return h;
}再贴一个moveRedRight(删除最大值或者任意值用到)
private Node moveRedRight(Node h)
{
flipColors(h);
if(!isRed(h.left.left))
h = rotateRight(h);
return h;
}其中banlance函数(删除后,修复红黑树)实现如下:
/**
* balance函数,相对于put操作的配平,是不是有点差异呢
* 其实都是可以的,差异只是:put操作的配平的第一个if判断,仅会将3-结点配平
* 而在这里的if,3-结点和4-结点都在第一个if进行首先配平了
* @param h
* @return
*/
private Node balance(Node h)
{
if(isRed(h.right))
h = rotateLeft(h);
if(isRed(h.left) && isRed(h.left.left))
h = rotateRight(h);
if(isRed(h.left) && isRed(h.right))
flipColors(h);
h.N = size(h.left)+size(h.right)+1;
return h;
}删除最大值当然就类似,下面直接讨论删除任意值。
3. 删除任意键
只要领悟了删除最小值,删除任意值,也就不难了。
与删除最小键值类似,必须确保删除的结点不是2-结点。
1>当删除节点是位于底部时,可以直接删除;不是底部,则和上一篇文章,删除二叉搜索树的结点类似。
2>假如不在底部,删除后我们显然要在它的子树中找到最小值进行替换
3>问题就变成了在一颗根结点不是2-结点的子树中删除最小值了。
4>删除后,仍需使用回溯并分解剩余的4-结点。
实现:
public void delete(Key key) {
if (get(key) == null) //需要删除的键值存不存在呢?
return;
if (!isRed(root.left) && !isRed(root.right))
root.color = RED;
root = delete(root, key);
if (!isEmpty()) root.color = BLACK;
}
private Node delete(Node h, Key key) {
if (key.compareTo(h.key) < 0) {
//和删除最小值类似
if (!isRed(h.left) && !isRed(h.left.left))
h = moveRedLeft(h);
h.left = delete(h.left, key);
}
else {
//咦?左子树有一个红链接?那右子树是不是肯定比左子树高度少1了(不可能左右都是红链接)
//deleye(h.right,key)?那不行了,这样左右子树肯定不是黑色平衡了
if (isRed(h.left))
h = rotateRight(h);
//根结点就可以直接删除了
if (key.compareTo(h.key) == 0 && (h.right == null))
return null;
//
if (!isRed(h.right) && !isRed(h.right.left))
h = moveRedRight(h);
//这个就是非根结点的删除了
if (key.compareTo(h.key) == 0) {
Node x = min(h.right);
h.key = x.key;
h.val = x.val;
h.right = deleteMin(h.right);
}
else h.right = delete(h.right, key);
}
return balance(h);
}参照网站:http://algs4.cs.princeton.edu/30searching/
算法第四版