大整数相乘 分治法 和 循环暴力法

题目描述

有两个用字符串表示的非常大的大整数,算出他们的乘积，也是用字符串表示。不能用系统自带的大整数类型。

输入描述:

空格分隔的两个字符串，代表输入的两个大整数

输出描述:

输入的乘积，用字符串表示

示例1

输入

复制

72106547548473106236 982161082972751393

输出

复制

70820244829634538040848656466105986748



思路分析

例如x=1234,y=567

①将x拆分成两半儿，a = 12   b = 34
②将y拆分成两半儿，c = 5   d = 67
③则x*y = (12*102+34)*(5*102+67) = (a*102+b)*(c*102+d) = a*c*104+a*d*102+b*c*102+b*d

④递归求（a*c）,(a*d),(b*c),(b*d)的结果，
　　如果a,b，c，d足够小，就直接相乘算出结果，
　　否则，从第①步开始重复，继续拆分a，b，c，d，
　　直至到了能直接算结果的时候，递归结束，开始回溯

 

 

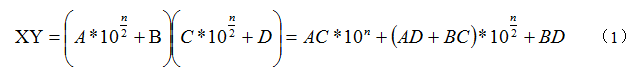
综上所述，java代码如下

import java.util.Arrays;
import java.util.Scanner;
public class Main {
    public static void main(String[] args){
        Scanner sca = new Scanner(System.in);
        String x = sca.nextLine();
        String y = sca.nextLine();
        System.out.println(f(x,y));
    }
    
    //分治法
    public static Long f(String x,String y){
        String a = x.substring(0, x.length()/2);
        String b = x.substring(x.length()/2);
        String c = y.substring(0, y.length()/2);
        String d = y.substring(y.length()/2);
        int n = b.length();
        int m = d.length();
        if(x.length()<=4 && y.length()<=4){
            return (long) (Integer.parseInt(x)*Integer.parseInt(y));
        }
        if(x.length()>4 && y.length()<=4){
            return (long) (f(a,y)*Math.pow(10, n)+f(b,y));
        }
        if(y.length()>4 && x.length()<=4){
            return (long) (f(c,x)*Math.pow(10, m)+f(d,x));
        }else{
            return (long) (f(a,c)*Math.pow(10, n+m)+f(a,d)*Math.pow(10, n)+f(b,c)*Math.pow(10, m)+f(b,d));
        }
    }
}

 

上述思路，时间复杂度是o(log_2^max(n,m))，其中n是x的长度，m是y的长度，

但是当最后的乘积超过long型的时候，还是会错误，

我一直没想到好的方法完全解决，百度了一下，试了好几个人的java代码，结果都是报错，有的甚至用long型变量接收输入的大整数，直接就报错了，没有一个是对的，访问量还那么高，真水啊，，，，，，

 

然后想了另一种方法，可以完美解决此问题，时间复杂度是o（n²）：

循环暴力法：

①把两个字符串经过拆分转换成int型数组

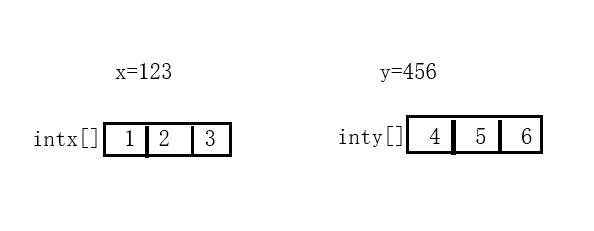
②用intx[]里的每个数字乘以inty[]里面的每一个数字，就是传统的在纸上手算的那个过程，将结果存入另一个数组

③如果两数相乘是两位数，就把十位上的数加到高位上。

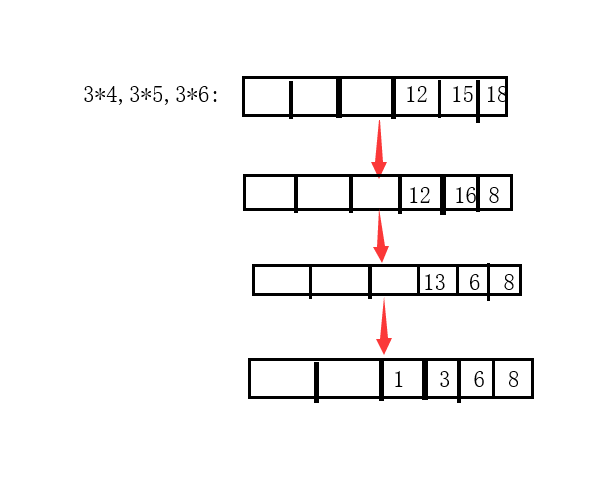
循环结束后，两个大数的乘积就按位数存到数组里了。

这个方法适用于所有的大数相乘。

java 代码如下

import java.util.Arrays;
import java.util.Scanner;
public class Main {
    public static void main(String[] args){
        Scanner sca = new Scanner(System.in);
        String x = sca.nextLine();
        String y = sca.nextLine();
        System.out.println(f(x,y));
    }
    public static String f(String x,String y){
        int[] intx = new int[x.length()];
        int[] inty = new int[y.length()];
        int[] intsum = new int[x.length()+y.length()];

        for (int i = 0; i < x.length(); i++) {
            intx[x.length()-1-i] = Integer.parseInt(x.substring(i, i+1));
        }
        for (int i = 0; i < y.length(); i++) {
            inty[y.length()-1-i] = Integer.parseInt(y.substring(i, i+1));
        }
        for (int i = 0; i < intx.length; i++) {
            for (int j = 0; j < inty.length; j++) {
                intsum[i+j] += intx[i]*inty[j];
            }
            for (int j = 0; j < intsum.length-1; j++) {
                if(intsum[j]>9){
                    intsum[j+1]+=intsum[j]/10;
                    intsum[j] = intsum[j]%10;
                }
            }
        }
        String str = "";
        boolean t = false;
        for (int i = intsum.length-1; i >=0; i--) {
            if(intsum[i]!=0) t = true;
            if(t) str = str+intsum[i];
        }
        return str;
    }
}