#include <iostream> //从A到C
using namespace std;
int n;
void ready() { cout << "请输入汉诺塔高度:"; cin >> n; cout << "默认从A移动到C" << endl; }
void move_recursion(int n, char des, char now, char temp) {
if (n == 1) { cout << 1 << "->" << des << endl; return; }
move_recursion(n - 1, temp, now, des);
cout << n << "->" << des << endl;
move_recursion(n - 1, des, temp, now);
}
void move_iterate(int n,char des, char now, char temp){
char inorder[2][4]={'0',temp,des,now,'0',des,now,temp};
int i,j,k;
char *np=new char[n+1];
for(int i=0;i<n+1;i++)np[i]='A';
for( i=1;i<(1<<n);i++){
for( j=i,k=1;j%2==0;k++,j/=2);
cout<<k<<" "<<np[k]<<"->";
np[k]=inorder[(1+n+k)%2][np[k]-'A'+1];
cout<<np[k]<<endl;}
}
int main(){
while (1) { ready(); move_iterate(n, 'C','A','B'); }
}
这上面的代码是我自己写的,迭代的过程参考了下面的代码,你们看不明白很正常。
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
http://blog.csdn.net/silence_rui/article/details/19141519 直接模仿栈的迭代方法
#include <iostream> //从A到C
#include <stack>
struct Quad {
Quad();
Quad(int n, char a, char b, char c): _n(n), _x(a), _y(b), _z(c) {
}
int _n; // 要移动的盘子数量
char _x, _y, _z; // 保存柱子名称
}; // 保存当前状态
void hanoi(int, char, char, char);
int main(int argc, char *argv[])
{
hanoi(3, 'A', 'B', 'C');
return 0;
}
void hanoi(int n, char x, char y, char z)
{
std::stack<Quad> s;
s.push(Quad(n, x, y, z));
while (!s.empty()) {
Quad q = s.top();
s.pop();
n = q._n;
x = q._x;
y = q._y;
z = q._z;
if (n == 1) {
std::cout << "Move top disk from peg " << q._x
<< " to peg " << q._z << "
";
}
else {
s.push(Quad(n - 1, y, x, z));
s.push(Quad(1, x, y, z));
s.push(Quad(n - 1, x, z, y));
}
}
}
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
http://blog.sina.com.cn/s/blog_48e3f9cd01000474.html 另一种迭代的方法
表示把n个盘子从src上借助via移动到des上。
显然有
void Hanoi(char src, char des, char via, int n)
{
Hanoi(src, via, des, n - 1);
Move(src, des, n); //把第n个盘子直接从src移动到des
Hanoi(via,des, src, n - 1);
}
那么显然 f(n + 1) = 2*f(n) + 1 -> [f(n + 1) + 1] = 2*[f(n) + 1]
f(1) = 1,-> f(n) + 1 = (1 + 1)^n -> f(n) = 2^n - 1。
f(64)= 2^64-1=18446744073709551615
假如每秒钟一次,共需多长时间呢?一年大约有 31536926 秒,计算表明移完这些金片需要5800多亿年,比地球寿命还要长,事实上,世界、梵塔、
定义从小到大的盘子序号分别为1,2,……n。
可以用一个1到2^n - 1的2进制序列可以模拟出n个盘子的汉诺塔过程中被移动的盘子的序号序列。
判断方法:第m步移动的盘子序号是m用二进制表示的最低位bit为1的位置。
假设n = k 成立。
n = k + 1时,对应序列1到2^(k+1) - 1,显然这个序列关于2^k左右对称。
假设我们要把k + 1个盘子从A移动C。
那么2^k可以对应着Move(k + 1, A, C)。 1 到 2^k - 1 根据假设可以
对应Hanoi(A, B, C, k)。至于2^k + 1 到 2^(k + 1) - 1把最高位的1去掉对应序列变成1到2^k - 1,显然2^k + 1 到 2^(k + 1) - 1和1到2^k - 1这两个序列中的对应元素的最低位bit为1的位置相同。因此2^k + 1 到 2^(k + 1) - 1可以对应Hanoi(B, C,A,k)。
所以对n = k + 1也成立。
定义顺序为 A->B->C->A, 逆序为C->B->A->C。
比如:n = 3
1 A->C
2 A->B
1 C->B
3 A->C
1 B->A
2 B->C
1 A->C
其中1的轨迹A->C->B->A>C逆序,2的轨迹A->B->C顺序,3的轨迹A->C逆序
证明:假设n <= k成立
对于n = k + 1 根据递归算法
Hanoi(A,C,B,k + 1) = Hanoi(A, B, C, k) + Move(A, C, k + 1) + Hanoi(B, C,A,k);
m盘子的移动由两部分组成一部分是前半部分Hanoi(A, B, C, k)以及后半部分的Hanoi(B, C,A,k)组成。显然有如果m在Hanoi(A, C, B, k)轨迹顺序的话,则m在Hanoi(A, B, C, k)以及Hanoi(B, C,A,k)都是逆序。反之亦然。这两部分衔接起来就会证明m在Hanoi(A,C,B,k)和Hanoi(A,C,B,k + 1)中是反序的。
同时有Hanoi塔中最大的盘子永远是逆序且只移动1步,A->C。
这样的话:
m = k,由于在Hanoi(A,C,B,k)中是逆序的,所以Hanoi(A,C,B,k + 1)中是顺序的。
m = k - 1,由于在Hanoi(A,C,B,k - 1)是逆序的,所以Hanoi(A,C,B,k)是顺序的,所以Hanoi(A,C,B,k + 1)是逆序的。
依次下去……
结论得证。
#include<iostream>//从A到C
#include<cstring>
using namespace std;
int main()
{
int n;
cin >> n;
char order[2][256];
char pos[64];
order[0]['A'] = 'B';
order[0]['B'] = 'C';
order[0]['C'] = 'A';
order[1]['A'] = 'C';
order[1]['B'] = 'A';
order[1]['C'] = 'B';
//0是顺序 1是逆序
int index[64];
//确定轨迹的顺序还是逆序
int i, j, m;
for(i = n; i > 0; i -= 2)
index[i] = 1;
for(i = n - 1; i > 0; i -= 2)
index[i] = 0;
memset(pos, 'A', sizeof(pos));
for(i = 1; i < (1 << n); i ++)
{
for(m = 1, j = i; j%2 == 0; j/=2, m ++);
cout << m <<" : "<< pos[m] <<" --> " << order[index[m]][pos[m]] << endl;
pos[m] = order[index[m]][pos[m]];
}
return 0;
}
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
http://blog.sina.com.cn/s/blog_65bda7120100khyg.html 还有一种迭代的方法
1、确定哪一个盘子要移动。
有n个盘子的Hanoi塔需要移动2^n -1次,设m为n位的二进制数,则m的取值范围为0~2^n -1。让m每次递增1,可以发现,m中最低一位的刚刚由0变为1的位置的位置编号,和即将要移动的盘子编号有确定关系。
2、这个盘子往哪个柱子上移。
a.第一次需要移动1号盘,n为奇数时,1号盘首先移动到柱子B,为偶数时首先移动到柱子C。
b.接下来如果移动的盘子不是1号盘。你有两个柱子可以选择。先找到1号盘所在的柱子,因为移动的盘子不能叠放到1号盘上,所以该盘可以移动的位置就是没有1号盘的那个柱子。
c.如果移动的盘子是1号盘。也有两个柱子可以选择。找到1号盘原先是从哪个柱子上移来的,因为移动的顺序(顺时针或逆时针)一旦确定,就不会更改,所以排除from的那个柱子后,移动方向也就唯一了。
#include <iostream>//从A到B
#include <stdlib.h>
#ifdef _WIN32
using namespace std;
#endif
static void hanoi(int height)
{
int fromPole, toPole, Disk;
int *BitStr = new int[height], //用来计算移动的盘的号码
*Hold = new int[height]; //用来存贮当前的盘的位置。hold[0]为第一个盘所在的柱号
char Place[] = {'A', 'C', 'B'};
int i, j, temp;
for (i=0; i < height; i++)
{
BitStr[i] = 0;
Hold[i] = 1;
}
temp = 3 - (height % 2); //第一个盘的柱号
int TotalMoves = (1 << height) - 1;
for (i=1; i <= TotalMoves; i++)
{
for (j=0 ; BitStr[j] != 0; j++) //计算要移动的盘
{
BitStr[j] = 0;
}
BitStr[j] = 1;
Disk = j+1;
if (Disk == 1)
{
fromPole = Hold[0];
toPole = 6 - fromPole - temp; //1+2+3等于6,所以6减去其它两个,剩下那个就是要移去的柱子
temp = fromPole; //保存上一次从哪个柱子移动过来的
}
else
{
fromPole = Hold[Disk-1];
toPole = 6 - Hold[0] - Hold[Disk-1];
}
cout << "Move disk " << Disk << " from " << Place[fromPole-1]
<< " to " << Place[toPole-1] << endl;
Hold[Disk-1] = toPole;
}
}
int main(int argc, char *argv[])
{
cout << "Towers of Hanoi: " << endl
<< "moving a tower of n disks from pole A to pole B by using pole C" << endl;
cout << "Input the height of the original tower: ";
int height;
cin >> height;
hanoi(height);
system("PAUSE");
return EXIT_SUCCESS;
}
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
https://www.cnblogs.com/whyandinside/archive/2012/08/18/2645602.html 还有一种用二叉树的迭代方法
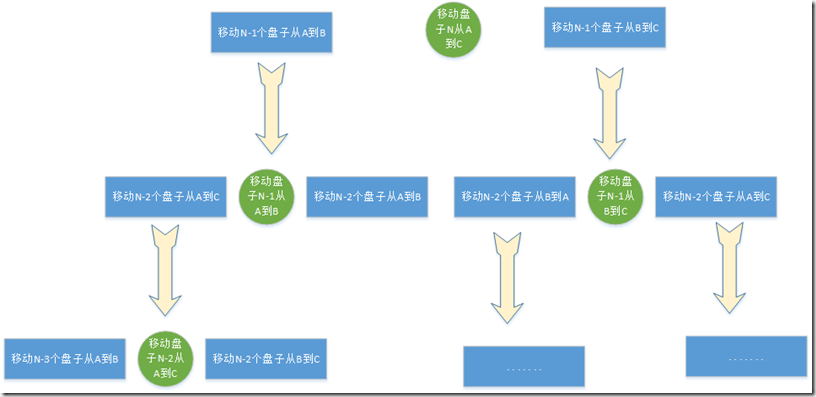
1. 我们先来分析一下移动的过程:先将n-1个盘子从A移动到B,把第n个盘子从A移动到C,把n-1个盘子从B移动到C。这本是递归的过程,但我们要想知道迭代操作的最终的数据结构,就一定要将其展开为原子操作。下面用图来解释:
这个图看起来就会更容易明白了,移动盘子的三个步骤就跟一个数一样,第一步移动若干盘子是左子树;第二步移动一个盘子相当于根;第三步移动若干盘子又相当于右子树。
而且每棵子树都可以按照同样的步骤分解,一直到全部是移动一个盘子的操作,至此,才算把整个数据结构展开了,我们也应该知道这是一个什么样的数据结构了:二叉树。
这个二叉树的深度是N,也就是盘子的个数,根节点表示盘子N的操作,孩子是N-1时的移动,. . . . 。移动的过程就是先左子树,根节点,右子树,也就是前序遍历。然后我们再看每个节点的表达式是什么?
画个图,看了一下,要找到每个节点的表达式是不容易的。不过,我们应该可以发现一个重要线索:只要最左面的节点知道了,就可以知道父节点和兄弟节点的表达式了。比如左孩子是m,A,B,那父节点是m+1,A,C, 右孩子是m,B,C。 所以关键就是要知道最左孩子的表达式。列出N = 1, 2,3 时的操作顺序可以发现,最左孩子只是在A,B和A,C之间交替。而且N为偶数时,为A,B;N为奇数时为A,C。至此我们对我们要迭代的数据结构就足够清楚了。下面就是实现一个满二叉树的前序遍历算法了。代码实现如下所示:
#include <iostream>//从A到C
#include <stack>
using namespace std;
class TreeNode
{
public:
TreeNode(int N, char _src, char _dest){ plateNum = N;src =_src; dest = _dest;}
int plateNum;
char src;
char dest;
};
void hanoi(int N)
{
stack<TreeNode *> *_stack = new stack<TreeNode *>();
_stack->push(new TreeNode(N, 'A', 'C'));
TreeNode * current = _stack->top();
while(!_stack->empty())
{
while(current->plateNum > 0)
{
current = new TreeNode(current->plateNum-1,current->src,'A'+'B'+'C' - current->dest - current->src);
_stack->push(current);
}
current = _stack->top();
_stack->pop();
cout<<"Move "<<(current->plateNum+1)<<" from "<<current->src<<" to "<<current->dest<<endl;
if(current->plateNum != 0)
{
TreeNode* old = current;
current = new TreeNode(current->plateNum-1,'A'+'B'+'C' - current->dest - current->src, current->dest);
_stack->push(current);
delete old;
}
}
delete _stack;
}
int main(int argc, char **argv)
{
int N;
char src = 'A',resource='B',dest = 'C';
bool moved = false;
cout<<"Please input a number:"<<endl;
cin>>N;
hanoi(N-1);
}